Các thiết bị quang học là hệ thống quang học được tạo nên bởi nhiều loại dụng cụ quang học như thấu kính, bản mặt song song, gương, v.v. Vai trò của chúng là rất lớn trong việc nghiên cứu các hiện tượng vật lý. Đây là những nghiên cứu về thế giới vi mô sử dụng kính hiển vi, nghiên cứu các ngôi sao và thiên hà bằng kính thiên văn và kính ngắm cũng như quan sát các vật thể ở xa bằng ống nhòm, chụp ảnh các vật thể bằng máy ảnh, nghiên cứu tính chất điện môi của môi trường khác nhau. Một trong những yêu cầu chính đối với các thiết bị như vậy là yêu cầu biến đổi các tia phát ra từ vật thể thành các tia hội tụ tại một điểm: quan sát (ảnh thật) hoặc thành các tia phân kì (tạo ảnh ảo). Bài tập các dụng cụ quang được cấu tạo từ hệ thấu kính hoặc hệ thấu kính - gương phẳng rất đa dạng và thực tế, chúng được sử dụng nhiều cho các kì thi học sinh giỏi Vật lí, ở mọi cấp độ. Bài viết này giới thiệu đến các bạn những bài tập các dụng cụ quang được cấu tạo từ hệ thấu kính hoặc hệ thấu kính - gương phẳng được tuyển chọn từ các kì thi môn vật lý, phương pháp giải rất sáng tạo chủ yếu dựa trên cách xây dựng đường đi của tia sáng từ các vật đến ảnh của chúng.
1 Các bài toán chọn lọc về các dụng cụ quang được cấu tạo từ hệ thấu kính hoặc hệ thấu kính - gương phẳng
Bài toán 1 . Dùng phép vẽ xác định tiêu điểm chính các thấu kính
Thấu kính phân kì $Л_1$ và thấu kính hội tụ $Л_2$ đặt trên cùng một trục quang chính (Hình 1). Hệ quang học như vậy tạo ra ảnh thật $A_1B_2$ của vật $AB$. Sử dụng phép vẽ, hãy tìm vị trí của các tiêu điểm chính.
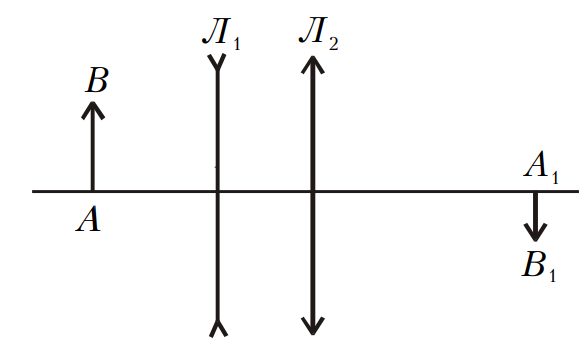
Ta làm theo các bước sau:
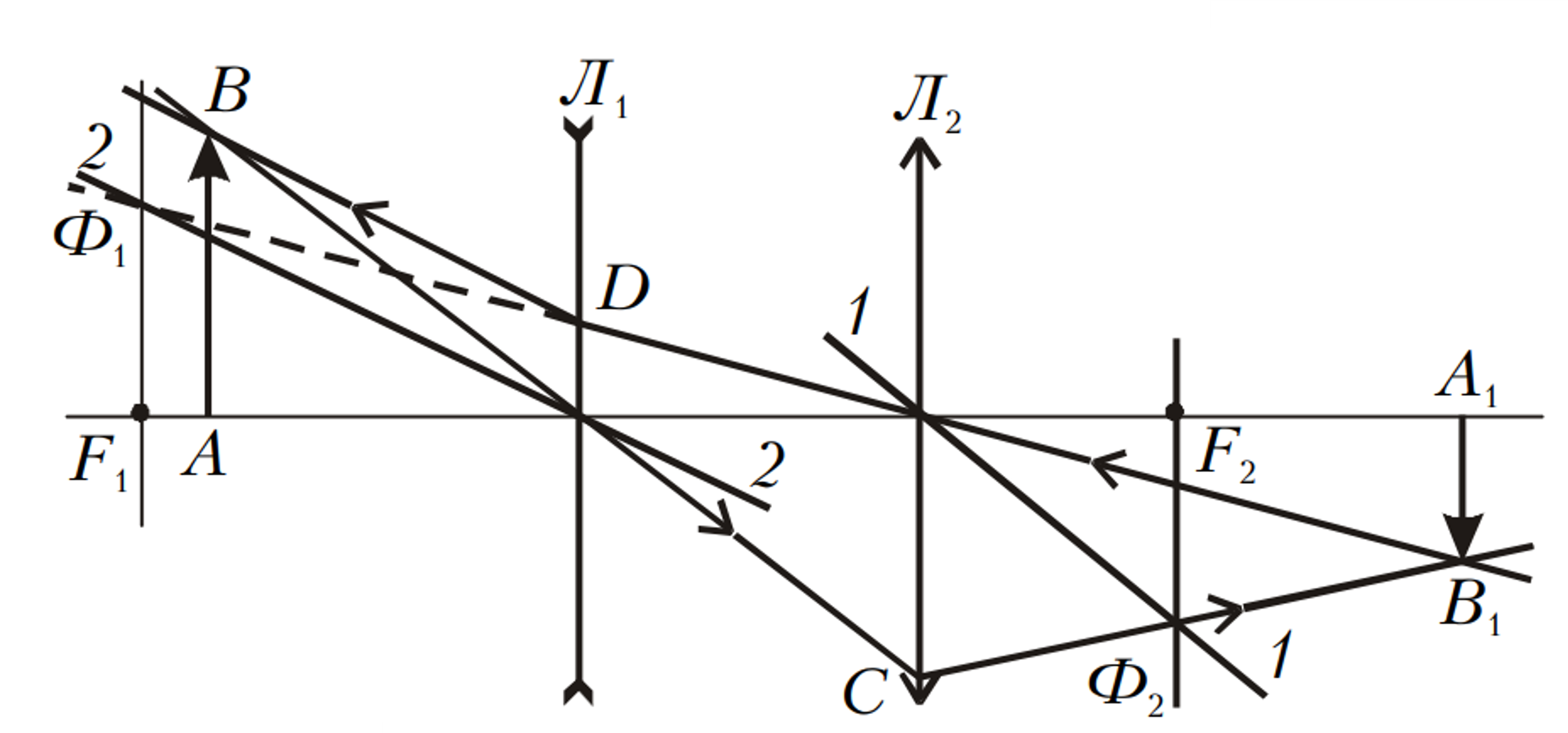
+ Vẽ một tia từ điểm $B$ qua quang tâm thấu kính $Л_1$ thì tia đi thẳng cho đến khi nó cắt thấu kính $Л_2$ tại điểm $C$ (Hình 2). Sau khi khúc xạ bởi thấu kính $Л_2$, tia này sẽ đi theo đường $CB_1$.
+ Từ điểm $B_1$ ta vẽ tia đi qua quang tâm thấu kính $Л_2$, tia này đi thẳng đến gặp thấu kính $Л_1$ tại $D$, sau khi khúc xạ bởi thấu kính $Л_1$, nó sẽ đi theo hướng $DB$.
+ Qua quang tâm thấu kính $Л_2$ vẽ đường thẳng $1 - 1$, song song với BC cắt đường $CB_1$ tại $Φ_2$, điểm này nằm trong tiêu diện của thấu kính $Л_2$, giao điểm của tiêu diện này với trục quang chính của hệ thống xác định vị trí của tiêu điểm bên phải $F_2$ của thấu kính $Л_2$.
+ Bây giờ chúng ta hãy tìm tiêu điểm bên trái của thấu kính. Để làm điều này, chúng ta vẽ một đường thẳng $2 - 2$ song song với tia $BD$, nó cắt đường kéo dài của tia $B_1D$ tại điểm $Φ_1$, sẽ xác định vị trí tiêu diện của của thấu kính $Л_1$. Giao điểm của mặt phẳng này với trục quang chính của hệ đặt vị trí của tiêu điểm bên trái $F_1$ của thấu kính $Л_1$.
Bài toán 2 . Tác dụng của ống kính lắp thêm cho máy ảnh
Văn bản của một bài báo được chụp bằng máy ảnh có ống kính tiêu cự $f=50\ \text{cm}$. Máy chụp được ảnh rõ nét ở khoảng cách gần nhất là $d=0\text{,}5\ \text{m}$. Khi lắp thêm ống kính ngoài cho máy ảnh, hệ thấu kính của máy và ống kính lắp thêm tương đương với một thấu kính có tiêu cự vẫn bằng $f$ nhưng khoảng cách từ thấu kính tương đương đến phim ảnh đã tăng thêm $h=25\ \text{mm}$ so với khi chưa lắp thêm ống kính. Và tất nhiên khoảng cách gần nhất có thể chụp ảnh rõ nét cũng thay đổi thành $d_1$. Xác định tỉ lệ kích thước ảnh chụp với máy chưa lắp thêm ống kính và ảnh chụp với máy đã lắp thêm ống kính. Biết răng cả hai lần chụp đều đặt vật ở khoảng cách gần nhất có thể.
Độ phóng đại của ảnh khi chưa lắp thêm ống kính là $$k=\frac{f}{f-d}$$ Khi đã lắp thêm ống kính, dộ phóng đại của ảnh là $$k_1=\frac{f-d_1^{'}}{f}$$ Trong đó $$d_1^{'}=d^{'}+h=\frac{df}{d-f}+h$$ Tức là $$k_1=\frac{f^2+dh-hf}{f\left(f-d\right)}$$ Tỉ lệ kích thước các ảnh $$Γ=\frac{k_1}{k}=\frac{f^2+dh-hf}{f^2} =5\text{,}5$$
Bài toán 3 . Quan sát Mặt trăng bằng kính thiên văn
Người quan sát có thị lực bình thường, quan sát Mặt trăng qua kính thiên văn, vật kính có tiêu cự $f_1=2\ \text{m}$ và thị kính có tiêu cự $f_2=5\ \text{cm}$. Mắt của người quan sát được điều tiết để ngắm chừng ở điểm cực cận cách mắt $d_0=25\ \text{cm}$.
-
Xác định khoảng cách giữa vật kính và thị kính.
Phải dịch chuyển thị kính một khoảng bằng bao nhiêu để thu được ảnh Mặt trăng trên màn phía sau thị kính một khoảng $d_0=25\ \text{cm}$? Khi đó kích thước của hình ảnh Mặt trăng trên màn là bao nhiêu nếu góc trông của nó là $α=30'$?
1. Khoảng cách giữa vật kính và thị kính khi ngắm chừng ở cực cận
Mặt trăng ở xa vô cực nên ảnh $SS$ của nó qua vật kính $Л_1$ nằm trên tiêu diện ảnh của thấu kính này. Ảnh $SS$ cách thị kính $Л_2$ một khoảng $d_1$ như Hình 3.
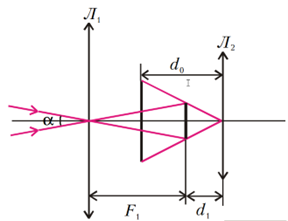
Áp dụng công thức thấu kính cho sự tạo ảnh của thị kính $$d_1=\frac{{-d}_0f_2}{-d_0-f_2}$$ Trong đó dấu “$-$” xuất hiện phía trước $d_0$ là vì ảnh $S_1S_1$ là ảnh ảo. Thay số ta tính được $$d_1=\frac{25.5}{25+5}=4\text{,}17\ \mathrm{\mathrm{cm}}$$ Khoảng cách giữa vật kính và thị kính là $$\Delta=f_1+d_1=204\text{,}7\ \mathrm{\mathrm{cm}}$$
2. Khoảng dịch chuyển thị kính để thu được ảnh thật cách thị kính $d_0=5\ \mathrm{\mathrm{cm}}$
Ảnh thật thu được qua thị kính được biểu diễn bằng Hình 4 dưới đây:
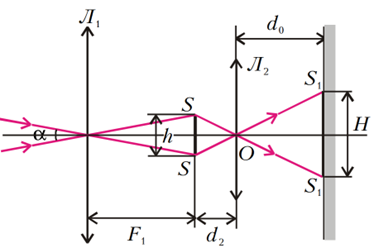
Vẫn công thức thấu kính nhưng bây giờ không có dấu “$-$” như tình huồng trước, tức là $$d_2=\frac{d_0f_2}{d_0-f_2}=\frac{25.5}{25-5}=6\text{,}25\ \mathrm{\mathrm{cm}}$$ Thị kính phải dịch chuyển một khoảng $$\Delta d=d_2-d_1=2\text{,}08\ \mathrm{\mathrm{cm}}$$ Biết góc trông của Mặt Trăng, người ta dễ dàng tìm được kích thước của ảnh của nó. Từ đồng dạng nhau của các tam giác $\Delta SSO$ và $\Delta S_1S_1O$ ta thu được $$H=\frac{d_0}{d_2}h$$ Trong đó với góc nhỏ $\alpha$ ta có thể tính $h$ bằng $$h=\alpha\ f_1$$ Tức là $$H=\alpha\ f_1\frac{d_0}{d_2}=7\ \mathrm{\mathrm{cm}}$$
Bài toán 4 . Hệ thấu kính – gương phẳng
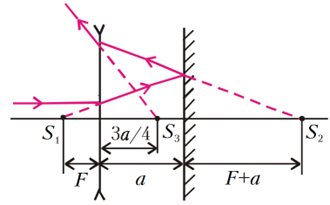
Một chùm tia song song từ một nguồn ở xa nằm trên trục chính chiếu tới một thấu kính phân kì mỏng. Cách thấu kính một khoảng $a$, vuông góc với trục chính của nó, có đặt một gương phẳng. Sau khi tia sáng đi qua thấu kính, bị phản xạ khỏi gương và lại đi qua thấu kính, tạo thành một ảnh ảo, nằm giữa thấu kính và gương và cách thấu kính $\frac{3a}{4}$. Xác định tiêu cự của thấu kính.
Một chùm tia song song từ một nguồn ở xa khi đi qua một thấu kính phân kì sẽ tạo ra một ảnh ảo $S_1$‚ nằm ở tiêu điểm của thấu kính (Hình 5). Ảnh $S_2$ của $S_1$ qua gương nằm cách thấu kính một khoảng $2a+|f|$ và là một “vật” đối với thấu kính, cho ảnh ảo tại điểm $S_3$. Áp dụng công thức thấu kính cho $S_2$ và $S_3$ ta có $$\frac{1}{2a-f}-\frac{4}{3a}=\frac{1}{f}$$ Trong đó $\left|f\right|=-f$ vì thấu kính phân kì có $f\lt 0$; $-\frac{4}{3a}$ vì ảnh là ảnh ảo. Ta viết lại phương trình thành $$2f^2-af-3a^2=0$$ Giải ra ta được $$f=-a,f=\frac{3a}{2}$$ Như đã nói ở trên, thấu kính phân kì có $f\lt 0$ nên ta chọn $f=-a$.
Bài toán 5 . Hệ thấu kính – thấu kính
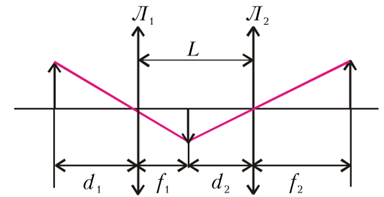
Hai thấu kính mỏng đặt cách nhau $L=25\ \mathrm{\mathrm{cm}}$ sao cho trục chính của chúng trùng nhau. Hệ thấu kính này tạo ra ảnh thật, cùng chiều và có kích thước bằng của vật. Nếu đổi chỗ các thấu kính mà không làm thay đổi vị trí của vật thì thu được ảnh thật cùng chiều với vật đó, nhưng với độ phóng đại $Г=4$. Độ tụ của các thấu kính chênh lệch nhau bao nhiêu?
Dễ dàng nhận thấy nếu ảnh của một vật là ảnh thật cùng chiều vật (Hình 6) thì cả hai thấu kính đều là thấu kính hội tụ.
Độ phóng đại của thấu kính $Л_1$ bằng $$\Gamma_1=\frac{F_1}{F_1-d_1}$$ Đối với ống kính Л2, nó bằng \begin{align} \Gamma_2&=\frac{F_2}{F_2-d_2}\\ &=\frac{F_2}{F_2-L+f_1}\\ &=\frac{F_2}{F_2-L+\frac{d_1F_1}{d_1-f_1}} \end{align} Độ phóng đại của hệ gồm hai thấu kính là \begin{align} \Gamma&=\Gamma_1\Gamma_2\\ &=\frac{F_1F_2}{d_1\left(L-\left(F_1+F_2\right)\right)+F_1F_2-F_1L} \end{align} Hay $$\frac{1}{\Gamma}=\frac{d_1\left(L-\left(F_1+F_2\right)\right)+F_1F_2}{F_1F_2}-\frac{L}{F_2}$$ Trong trường hợp hoán đổi thấu kính, độ phóng đại là $\Gamma_\ast$, ta viết $$\frac{1}{\Gamma_\ast}=\frac{d_1\left(L-\left(F_1+F_2\right)\right)+F_1F_2}{F_1F_2}-\frac{L}{F_1}$$ Lấy hiệu của hai biểu thức cuối, ta có \begin{align} \frac{1}{\Gamma}-\frac{1}{\Gamma_\ast}&=L\left(\frac{1}{F_1}-\frac{1}{F_2}\right)\\ &=L\left(D_1-D_2\right) \end{align} Trong đó $D_1$ và $D_2$ là độ tụ của thấu kính $Л_1$ và $Л_2$. Cuối cùng, sự chênh lệch về độ tụ bằng \begin{align} \Delta D&=D_1-D_2\\ &=\frac{1}{L}\left(\frac{1}{\Gamma}-\frac{1}{\Gamma_\ast}\right)\\ &=3\ \mathrm{\mathrm{dp}} \end{align}
Bài toán 6 . Hệ thấu kính gương phẳng trong hộp
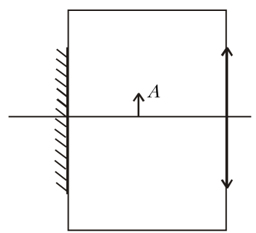
Một vật đặt giữa thấu kính và gương phẳng vuông góc với trục chính của thấu kính. Gương, thấu kính và vật được đặt trong một vỏ làm bằng nhựa mờ (Hình 7). Hệ thống như vậy tạo ra hai ảnh của một vật và một ảnh của thấu kính. Hai ảnh của vật đều có cùng kích thước, bất kể khoảng cách từ thấu kính đến vật. Ảnh của thấu kính có độ phóng đại bao nhiêu?
Gọi vật là $A_1$, ảnh của $A_1$ trong gương là $A_2$, thì hai ảnh mà bài toán đề cập ở đây chính là: Một ảnh của $A_1$ qua thấu kính ta đặt là $B_1$, ảnh còn lại $B_2$ là ảnh của $A_2$ cũng qua thấu kính (Hình 8).
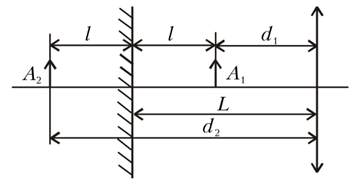
Vì cả hai hình ảnh đều có cùng kích thước nên độ phóng đại của chúng cũng bằng nhau. Trong khi đó khoảng cách từ các “vật” đến thấu kính khác nhau. Rõ ràng là điều này chỉ có thể xảy ra trong trường hợp một trong hai ảnh là ảnh thật và ảnh còn lại là ảnh ảo. Do đó, vật $A_1$ nằm giữa thấu kính và tiêu điểm của nó, còn vật $A_2$ nằm sau tiêu điểm của thấu kính.
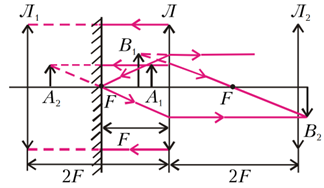
Ta sử dụng công thức thấu kính cho những trường hợp này: \begin{align} \frac{1}{F}=\frac{1}{d_1}+\frac{1}{f_1}\\ \mathrm{và}\ \frac{1}{F}=\frac{1}{2l+d_1}+\frac{1}{f_2} \end{align} Trong đó $f_1$ và $f_2$ là các khoảng cách đại số từ các ảnh $B_1$, $B_2$ đến thấu kính. Độ phóng đại ảnh tương ứng $$k_1=\frac{F}{F-d_1}\\ k_1=\frac{F}{F-d_1-2l}$$ Theo bài ra và lập luận ở trên thì $k_1=-k_2$, suy ra $$d_1+l=F$$ Tức là gương phải nằm trong mặt phẳng tiêu (tiêu diện) của thấu kính. Gọi ảnh của thấu kính qua gương là $Л_1$ thì ảnh cuối cùng của thấu kính qua hệ $Л_2$ chính là ảnh của $Л_1$ qua thấu kính. Tức là khoảng cách từ “vật” $Л_1$ đến thấu kính là $2F$, độ phóng đại là $$k=\frac{F}{F-2F}=-1$$
Bài toán 7 . Thấu kính tương đương
Một thấu kính phức tạp gồm hai thấu kính mỏng: một thấu kính hội tụ có tiêu cự $F_1=20\ \mathrm{cm}$ và một thấu kính phân kì có tiêu cự $F_2=-10\ \mathrm{cm}$, hai thấu kính đặt cách nhau $l=15\ \mathrm{cm}$. Qua thấu kính ta thu được ảnh Mặt Trời trên màn. Một thấu kính mỏng phải có tiêu cự bằng bao nhiêu để ảnh Mặt trời thu được nhờ nó có cùng kích thước?
Gọi $\alpha$ là góc trông Mặt trời. Ảnh của Mặt trời qua thấu kính thứ nhất nằm đúng tiêu điểm của nó và có kích thước (tính gần đúng do $\alpha$ rất nhỏ) $h=\alpha\ F_1$ (Hình 10). Khoảng cách từ ảnh này đến thấu kính thứ hai là $d=F_1-l$.
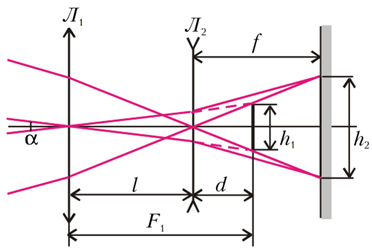
Từ công thức thấu kính $$\frac{1}{-\left(F_1-l\right)}+\frac{1}{f}=\frac{1}{F_2}$$ Tính khoảng cách từ màn đến thấu kính Л2: $$f=\frac{F_2\left(F_1-l\right)}{l-F_1-F_2}$$ Khi đó kích thước của ảnh thứ hai bằng: \begin{align} h_2&=h_1\frac{f}{d}\\ &=\frac{\alpha F_1F_2}{F_1-l+F_2} \end{align} Nếu sử dụng một thấu kính mỏng có tiêu cự $F$ thì kích thước ảnh của Mặt trời trong đó là $$h_2=\alpha\ F$$ Cuối cùng, đối với tiêu cự của thấu kính này, chúng ta thu được $$F=\frac{F_1F_2}{F_1-l+F_2}=40\ \mathrm{\mathrm{cm}}$$
2 Các bài toán tự giải về các dụng cụ quang được cấu tạo từ hệ thấu kính hoặc hệ thấu kính - gương phẳng
- Nguồn sáng nằm ở khoảng cách gấp đôi tiêu cự tính từ thấu kính hội tụ trên trục của nó. Một gương phẳng được đặt phía sau thấu kính vuông góc với trục chính. Hỏi gương phải đặt cách thấu kính một khoảng bao nhiêu để các tia phản xạ từ gương sau khi đi qua thấu kính lần thứ hai trở nên song song? Tiêu cự của thấu kính $F$.
- Chứng minh rằng độ tụ của một hệ gồm hai thấu kính mỏng đặt gần nhau bằng tổng độ tụ của hai thấu kính này.
-
Một gương phẳng (Hình 11) được đặt vuông góc với trục quang chính của một thấu kính hội tụ mỏng có tiêu cự $F$. Hệ thống quang học này tạo ra ảnh thật của vật $A$ nằm giữa thấu kính và tiêu điểm của nó, với độ phóng đại $k=\frac{F}{d}$, trong đó $d$ là khoảng cách giữa thấu kính và vật. Tìm khoảng cách giữa thấu kính và gương.
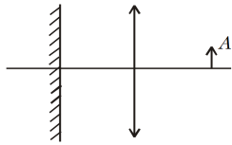
Hình 11: Hệ thấu kính hội tụ - gương phẳng dành cho bài 3. - Một hệ gồm hai thấu kính mỏng, hội tụ và phân kì, có tiêu cự cùng độ lớn $F$, tạo ra ảnh của một nguồn sáng điểm. Trục quang chính của thấu kính trùng nhau. Khoảng cách giữa các thấu kính $L=3F$. Nguồn được đặt trên trục quang chính ở khoảng cách $d=2F$ phía trước thấu kính hội tụ. Ảnh của nguồn sẽ dịch chuyển bao nhiêu và theo hướng nào nếu thấu kính hội tụ dịch chuyển vuông góc với trục quang chính một khoảng $x=2\ \mathrm{\mathrm{cm}}$?
- Một nguồn sáng điểm đặt cách thấu kính một khoảng $d=30\ \mathrm{\mathrm{cm}}$, có độ tụ $D=5\ \mathrm{\mathrm{dp}}$. Ảnh của nguồn sẽ dịch chuyển một khoảng bằng bao nhiêu nếu đặt một tấm thủy tinh dày có độ dày $L=15\ \mathrm{\mathrm{cm}}$ và chiết suất $n=1\text{,}572$ giữa thấu kính và nguồn?
- Do độ phân giải hữu hạn của phim chụp ảnh nên khi chụp ảnh, các vật nằm ở khoảng cách từ $d_1=15\ \mathrm{\mathrm{m}}$ đến $d_2=30\ \mathrm{\mathrm{m}}$ tính từ máy ảnh sẽ thu được nét rõ nét. Giá trị $d_1$ được gọi là giới hạn gần của độ sâu trường ảnh, $d_2$ được gọi là giới hạn xa. Không thay đổi hướng của máy ảnh, ống kính đã được mở khẩu (tức là đường kính của phần mở của ống kính đã giảm). Đồng thời, giới hạn gần của độ sâu trường ảnh trở thành: $d_1^\ast=10\ \mathrm{\mathrm{m}}$. Tìm giới hạn xa.
- Tìm tiêu cự tương đương của hệ gồm hai thấu kính có tiêu cự $F_1$ và $F_2$ nằm trên cùng một trục quang cách nhau một khoảng $l$ và vị trí của thấu kính tương đương.


0 nhận xét:
Đăng nhận xét