Đáp án đề thi học sinh giỏi Vật lý 12 tỉnh Nghệ An (bảng A - phần tự luận) năm học 2025 - 2026 là tài liệu tham khảo hữu ích dành cho các em học sinh lớp 12 yêu thích môn Vật lý đang ôn luyện cho kỳ thi học sinh giỏi cấp tỉnh.
Đề thi học sinh giỏi Vật lý 12 Nghệ An kèm lời giải chi tiết giúp học sinh nắm vững phương pháp tư duy, cách trình bày và vận dụng công thức vào các dạng bài khó. Đây cũng là nguồn tài liệu quý để các giáo viên tham khảo khi ra đề và hướng dẫn học sinh giỏi.
Trong tài liệu này, các câu hỏi được phân tích rõ ràng, đi kèm hướng dẫn giải chi tiết và công thức Vật lý 12 liên quan, giúp người học củng cố kiến thức nền tảng và rèn luyện khả năng lập luận logic.
Hy vọng bộ đáp án đề thi HSG Vật lý 12 Nghệ An 2025 - 2026 này sẽ giúp các em tự tin hơn trong quá trình ôn luyện và đạt kết quả cao trong kỳ thi tới!

Câu 1. Giao thoa ánh sáng - Đáp án đề HSG vật lý Nghệ An 2025 - 2026
1.1. Thí nghiệm Young
a) Giải thích vì sao người làm thí nghiệm thường đo khoảng cách giữa nhiều vân sáng mà không đo khoảng cách giữa hai vân sáng liên tiếp
Với cùng một dụng cụ đo, sai số tuyệt đối mỗi lần đo là tương đương nhau, ta đặt là $\Delta x$. Nếu đo khoảng cách giữa hai vân sáng liên tiếp thì giá trị đo là $x_1$, nếu đo khoảng cách giữa 9 vân sáng liên tiếp thì giá trị đo được là $x_9$, khi đó $x_9 \gt x_1$, dẫn đến sai số tỉ đối
$$
\frac{\Delta x}{x_9}\lt \frac{\Delta x}{x_1}
$$
Như vậy đo khoảng cách giữa nhiều vân sáng làm giảm sai số tỉ đối.
b) Xác định bước sóng $\lambda_1$
Khoảng cách giữa 9 vân sáng liên tiếp bằng 8 lần khoảng vân, suy ra khoảng vân
$$
i_1=\frac{18}{8}=2\text{,}25\ \mathrm{mm}
$$
Từ công thức khoảng vân $i_1=\dfrac{\lambda_1 D}{a}$ suy ra bước sóng
\begin{align}
\lambda_1&=\frac{ai_1}{D}\\
&=\frac{0\text{,}2\!\times\!2\text{,}25}{0\text{,}6}\\
&=0\text{,}75\ \text{mm}
\end{align}
c) Khoảng cách lớn nhất, nhỏ nhất giữa hai vân sáng khi chiếu đồng thời hai bức xạ vào hai khe
Hai vân sáng liên tiếp có thể là hai vân sáng của hai bức xạ khác nhau, cũng có thể là hai vân sáng của cùng một bức xạ. Nên khoảng cách giữa hai vân liên tiếp (ta đặt là $I$ không thể lớn hơn các khoảng vân, tức là
\begin{cases}
I\leq i_1\\
I\leq i_2
\end{cases}
Suy ra $I_\text{max}=i_1$ nếu $i_1\lt i_2$ và $I_\text{max}=i_2$ nếu $i_2\lt i_1$.
Theo bài ra thì $I_\text{max}=1\text{,}35\ \text{mm} \lt i_1$, tức là $I_\text{max}=i_2$.
Hai vân sáng gần nhau nhất chắc chắn phải là hai vân của hai bức xạ khác nhau (vì nếu cùng một bức xạ, khoảng cách đó là lớn nhất như đã phân tích ở trên). Ta giả sử đó là vân bậc $k_1$ của $\lambda_1$ và vân bậc $k_2$ của bức xạ $\lambda_2$. Khoảng cách giữa hai vân này là
\begin{align}
d&=|k_1 i_1-k_2i_2|\\
&=|2\text{,}25k_1-1\text{,}35k_2|\\
&=0\text{,}45 |5k_1-3k_2|
\end{align}
Do $k_1$ và $k_2$ đều là số nguyên nên $|5k_1-3k_2|$ là một số nguyên dương, giá trị nhỏ nhất của nó có thể được thử từ $1, 2, 3,...$.
Dễ dàng nhận thấy giá trị $1$ thoả mãn với $k_1=1,k_2=2$.
Vậy
$$
d_\text{min}=0\text{,}45\ \text{mm}
$$
1.2. Phương án thực hành với thí nghiệm Young
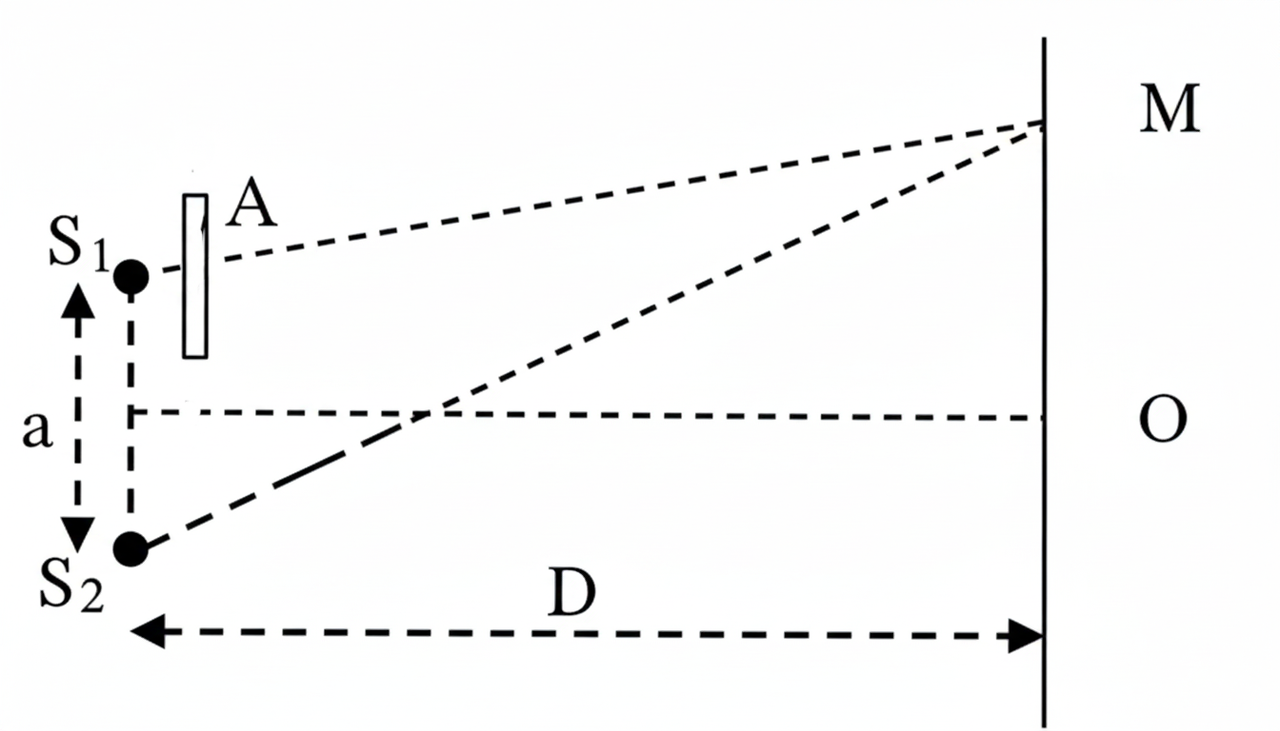
- Bước 1: Thực hiện thí nghiệm giao thoa Young, sử dụng hai tấm thủy tinh giống nhau đặt vào hai khe $\mathrm{S_1}$ và $\mathrm{S_2}$ không có phủ $\mathrm{TiO_2}$ đánh dấu vân trung tâm.
- Bước 2: Sử dụng một tấm thủy tinh không phủ $\mathrm{TiO_2}$ vào khe $\mathrm{S_1}$ và một tấm thủy tinh có phủ $\mathrm{TiO_2}$.
- Bước 3: Đo độ dịch chuyển của hệ vân ở bước 2 so với bước 1 là (dựa vào độ dịch chuyển của vân trung tâm đó là vị trí sáng nhất).
- Bước 4: Dùng dụng cụ thích hợp xác định khoảng cách từ mặt phẳng hai khe đến màn quan sát $D$, khoảng cách hai khe là $a$.
- Bước 5 : Độ dày của lớp $\mathrm{TiO_2}$ là:
$$
d=\frac{ax}{(n-1)D}
$$
Nhận xét: Nếu ai đã làm thí nghiệm với hai khe Young thì thấy bài toán thực hành này gần như không thể thực hiện được. Bởi lẽ, khoảng cách giữa hai khe được bố trí rất nhỏ (nhỏ đến mức chúng ta thấy hai khe như trùng nhau). Vậy nên không thể sử dụng các tấm thuỷ tinh phủ lớp mỏng để làm thí nghiệm như yêu cầu của bài toán.
Các thí nghiệm về chắn bản mỏng trước một khe Young được thiết kế riêng, rất tỉ mỉ. Việc đo độ dày bản mỏng nếu bằng phương pháp giao thoa ánh sáng người ta thường sử dụng cách bố trí khác, không phải thí nghiệm Young.
Câu 2. Ứng dụng điện trường trong máy in - Đáp án đề HSG vật lý Nghệ An 2025 - 2026
a) Điện trường tác dụng lực điện lên giọt mực để tăng tốc và định hướng chuyển động các giọt mực.
b) Lực điện tác dụng lên mỗi giọt mực: $$F = QE = 24\! \times\! 10^{-8}\ \text{(N)}$$
c) Khối lượng mỗi giọt mực: $$m = \rho V = 1{,}44\! \times\! 10^{-10}\ \text{(kg)}$$
Gia tốc mỗi giọt mực là: $$a = \frac{F}{m} = \frac{5}{3}\! \times\! 10^3\ \mathrm{(m/s^2)}$$
Thời gian rơi của một giọt mực là: $$t = \sqrt{\frac{2d}{a}} = 1{,}55\ \text{(ms)}$$
d) Số giọt mực được in trong 1 giây là: $$N = \frac{1}{t} \approx 645\ \text{giọt}$$
Thể tích phần mực in trong khối mô hình: $$V_0 = 40\% \!\times\! 10\! \times\! 10{,}5 = 2\! \times\! 10^2\ \mathrm{(mm^3)} = 2\! \times\! 10^{-7}\ \mathrm{(m^3)}$$
Thời gian in: $$t = \dfrac{V_0}{N \cdot V} \approx 2584\ \text{s} \approx 43\ \text{phút}$$
Câu 3. Đáp án đề HSG vật lý Nghệ An 2025 - 2026
3.1. Đế dày cách điện
a) Gọi \( R_{\text{ESD}} \) là điện trở của dây ta có:
$$U_{\text{ESD}} + U = E \;\Rightarrow\; U_{\text{ESD}} = E - U$$Thay số:
$$R_{\text{ESD}} = \dfrac{U_{\text{ESD}}}{U} R = \dfrac{E - U}{U} R = \dfrac{50 - U}{U} \;(\text{M}\Omega)$$b) Theo biểu thức trên (a), ta có:
$$R_{\text{ESD}} = \dfrac{50 - 0{,}0U}{U} = \dfrac{50 - 12}{12} = 3{,}17\ \text{M}\Omega$$→ Giày đáp ứng yêu cầu.
3.2. Nhiệt điện trở
a) Dòng điện chạy qua điện trở làm nóng điện trở. Điện trở tỏa nhiệt ra môi trường.
Nhiệt độ của điện trở ổn định khi công suất do điện trở tỏa ra môi trường bằng công suất do dòng điện cung cấp cho nó.
b) Ở nhiệt độ \( t_1 = 220^\circ\text{C} \), điện trở của thiết bị là: $$R_1 = \dfrac{U_1}{I_1} = 100\ \Omega$$
Điện trở gia nhiệt ở nhiệt độ phòng là: $$R_0 = \dfrac{R_1}{1 + \alpha (t_1 - t_0)} = 80\ \Omega$$
Công suất làm nóng là: $$P_1 = U_1 I_1 = 0{,}0144\ \text{W}$$
Hằng số k là: $$k = \dfrac{P_1}{t_1 - t_0} = 7{,}2\!\times\!10^{-5}\ (\text{W/K})$$
c) Ở điện áp \( U \), công suất làm nóng vẫn bằng công suất hao phí nhiệt.
Ta có: $$\dfrac{U^2}{R} = \dfrac{U^2}{R_0 + \alpha R_0 (t - t_0)} = k (t - t_0)$$
Thay số: $$\dfrac{0{,}8^2}{80 + 80 \times 1{,}25\!\times\!10^{-3}(t - 20)} = 7{,}2\!\times\!10^{-5}(t - 20)\\ t \approx 118{,}9^\circ\text{C} $$
Câu 4. Đáp án đề HSG vật lý Nghệ An 2025 - 2026
a) Trong 40 s đầu nhiệt độ không đổi. Kim loại đang nóng chảy.
- Kim loại nhận nhiệt lượng từ nguồn nung dùng phá vỡ liên kết giữa các phân tử chất rắn để chuyển sang thể lỏng.
- Nội năng của kim loại tăng. Giải thích: theo định luật I Nhiệt động lực học $$\Delta U = A + Q$$ Vì $$A = 0$$, kim loại nhận nhiệt $$Q > 0$$ nên $$\Delta U > 0$$.
b) Từ đồ thị, thời điểm tắt nguồn nung thì nhiệt độ của kim loại bắt đầu giảm: $$\tau_2 = 50\,\text{s}$$ và nhiệt độ $$t_2 = 248^\circ\text{C}$$.
c) Từ thời gian [0; 40] s: $$\lambda m = (P - P_x)\tau_1 \quad (1)$$
Từ thời gian [40; 50] s: $$c m (t_2 - t_1) = (P - P_x)(\tau_2 - \tau_1) \quad (2)$$
Từ (2) và (1) ta có: $$c = \dfrac{\lambda (\tau_2 - \tau_1)}{\tau_1 (t_2 - t_1)} = 500\,\dfrac{\text{J}}{\text{kg·K}}$$
d) Từ thời gian [50; 80] s: $$c m (t_1 - t_2) = P_x (\tau_3 - \tau_2) \quad (3)$$
Thay $$c$$ vào (3): $$P_x = \dfrac{c m (t_2 - t_1)}{\tau_3 - \tau_2} = 30\,\text{W}$$
Thời gian đông đặc hoàn toàn được tìm từ phương trình: $$\lambda m = P_x (\tau - \tau_3)\\ \Rightarrow \tau = \dfrac{\lambda m}{P_x} + \tau_3 = 200\,\text{s}$$
Kết luận: Bộ đáp án đề thi học sinh giỏi Vật lý 12 Nghệ An 2025 - 2026 (bảng A – phần tự luận) không chỉ giúp học sinh đối chiếu kết quả mà còn là nguồn tư liệu quý để rèn luyện kỹ năng giải bài tập nâng cao. Qua đó, các em có thể củng cố kiến thức trọng tâm, nắm vững các dạng bài thi HSG Vật lý 12 và chuẩn bị tốt hơn cho các kỳ thi tiếp theo.
Nếu bạn thấy tài liệu hữu ích, hãy chia sẻ bài viết để nhiều bạn cùng học, hoặc xem thêm các đề thi học sinh giỏi Vật lý 12 Nghệ An năm học 2024 - 2025 để luyện tập thêm nhé!
— Chúc các em học sinh ôn tập hiệu quả và đạt thành tích cao trong kỳ thi học sinh giỏi Vật lý! —