Trong vật lý, các tình huống có thể xảy ra (mặc dù hiếm) khi cùng một công thức có thể biểu diễn cho các nội dung khác nhau, tức là, mô tả các định luật vật lý khác nhau về cơ bản. Chúng ta hãy xem xét một trường hợp như vậy, đó là suất điện động cảm ứng trong định luật cảm ứng điện từ nổi tiếng do Faraday phát hiện, và suất điện động trên một đoạn dây dẫn chuyển động trong từ trường. Hai suất điện động này có chung một công thức tính nhưng dường như chúng khác nhau về bản chất.
Suất điện động cảm ứng trong định luật cảm ứng điện từ do Faraday phát hiện ra
Ý nghĩa vật lý của định luật Faraday là từ trường thay đổi theo thời gian sẽ tạo ra một điện trường xoáy. Cụ thể là khi từ thông ($\Phi$) thay đổi theo thời gian, xuyên qua bề mặt giới hạn bởi một vòng dây dẫn kín, cố định, trong dây dẫn này xuất hiện một suất điện động cảm ứng ($E_c$): $$E_c=-\frac{\Delta\Phi}{\Delta t}\ \ \ (*)$$
Suất điện động trên một đoạn dây dẫn chuyển động trong từ trường
Khi một đoạn dây dẫn chuyển động cắt ngang các đường sức của một từ trường thì trên đọan dây dẫn này cũng xuất hiện một suất điện động, người ta cũng hay gọi là suất điện động cảm ứng. Lý do xuất hiện suất điện động này là lực Lorentz, tức là lực tác dụng lên một điện tích chuyển động trong từ trường. Độ lớn của lực này bằng $$F_L=qvB\sin{\alpha}$$ trong đó $q$ là độ lớn của điện tích, $v$ là tốc độ chuyển động của nó, $B$ là độ lớn của vectơ cảm ứng từ của từ trường trong đó điện tích chuyển động, $\alpha$ là góc giữa vectơ $\vec{v}$ và $\vec{B}$. Hướng của lực Lorentz được xác định theo quy tắc bàn tay trái nổi tiếng.
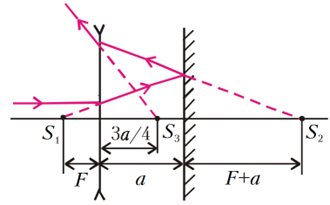
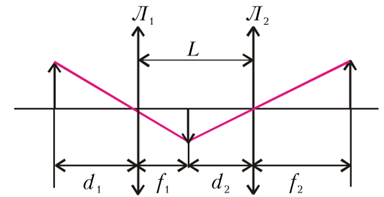
Chúng ta hãy xem xét trường hợp đơn giản nhất về chuyển động của một dây dẫn trong từ trường, như trong Hình 1. Dưới tác dụng của lực Lorentz, các êlectron tự do trong dây dẫn (tấm) chuyển động dồn về một đầu tấm, sao cho đầu dưới của tấm trở nên tích điện âm,
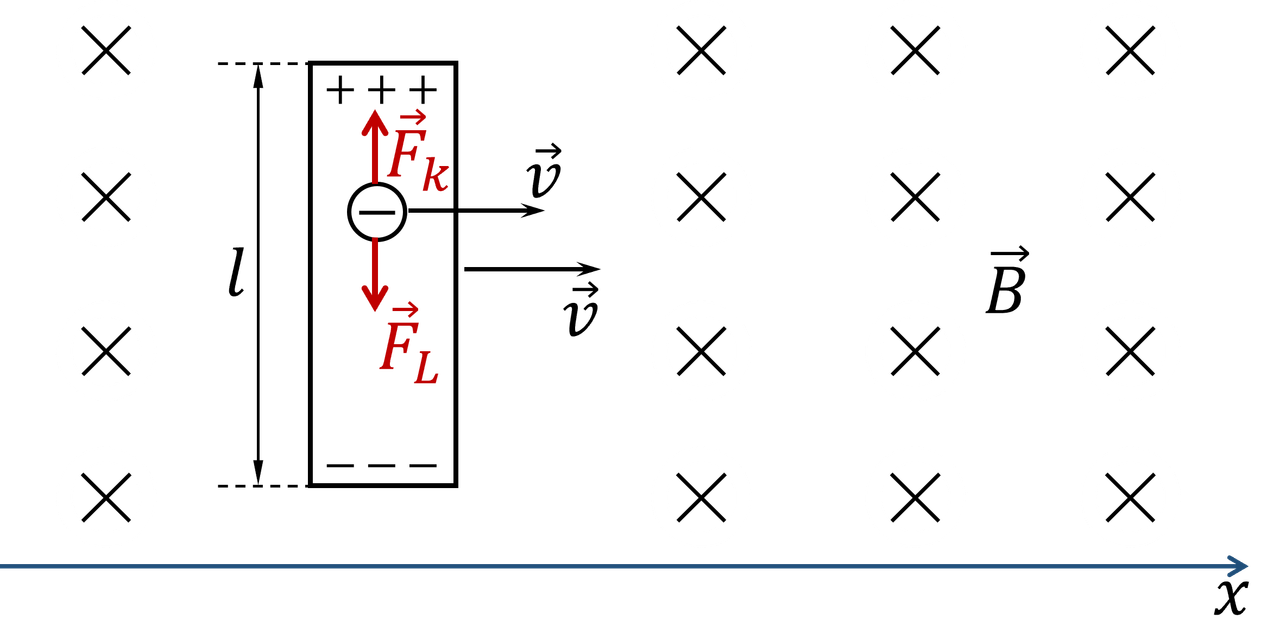
và đầu trên của tấm tích điện dương. Hai đầu thanh trở thành hai cực trái dấu, điện tích của các cực này có độ lớn tăng dần. Điều này xảy ra cho đến khi điện trường gữa hai cực đủ lớn, tác dụng lên các êlectron với lực Coulomb $\vec{F}_k$ có độ lớn bằng và ngược hướng với lực Lorentz $\vec{F}_L$. Lúc này điện tích của hai cực ổn định, hai cực này tương đương với một nguồn điện, suất điện động của nguồn điện này chính là suất điện động cảm ứng. Như vậy, tác dụng của lực Lorentz lên các điện tích tự do của một dây dẫn chuyển động trong từ trường sẽ dẫn đến xuất hiện suất điện động cảm ứng. Mặc dù suất điện động này không liên quan gì đến định luật cảm ứng điện từ Faraday, nhưng nó vẫn có thể được mô tả bằng cùng một công thức. Thật vậy, cường độ điện trường cảm ứng trong dây dẫn bằng \begin{equation} E=-\frac{F_{\text {L}}}{q}=-v B \end{equation} và suất điện động cảm ứng là \begin{align} \mathrm{E}_c&=E l\\ &=-v B l\\ &=-\frac{\Delta x}{\Delta t} B l\\ &=-\frac{\Delta \Phi}{\Delta t} \end{align} Nhưng trong trường hợp này, $\Delta \Phi$ được hiểu không phải là độ lớn của từ thông đi qua một dây dẫn chuyển động trong một mạch nhất định (như trong định luật Faraday), mà là độ lớn của từ thông đi qua diện tích mà sợi dây dẫn chuyển động quét được trong thời gian $\Delta t$. Đối với một mạch kín chuyển động hoặc biến dạng trong từ trường, $\Delta \Phi$ được hiểu là sự thay đổi của từ thông qua mạch này.
Tính suất điện động trong đoạn dây dẫn chuyển động bằng công thức suất điện động cảm ứng
Có thể sử dụng khái quát công thức tính suất điện động cảm ứng của định luật cảm ứng điện từ thay cho công thức tính suất điện động trong đoạn dây dẫn chuyển động trong từ trường. Bởi vì nếu dùng công thức $E=Bvl\sin{\alpha}$, trong trường hợp bài toán cho đoạn dây dẫn vừa chuyển động tịnh tiến vừa chuyển động quay thì thực sự rất phức tạp. Trong khi đó nếu dùng công thức suất điện động cảm ứng $E_c=-\frac{\Delta\Phi}{\Delta t}$, việc tích diện tích $S$ để rồi tính từ thông $\Delta \Phi$ đơn giản hơn rất nhiều. Sau đây ta giải một số bài toán tìm suất điện động trên một vật dẫn chuyển động trong từ trường nhưng sử dụng công thức định luật cảm ứng điện từ của Faraday.
Còn có chuyên đề hay dành cho các bạn đây:
GIẢI CÁC BÀI TOÁN VẬT LÍ BẰNG PHƯƠNG PHÁP QUY NẠPBài toán 1. Thanh kim loại quay trong một mặt phẳng trong từ trường với trục quay ở đầu thanh
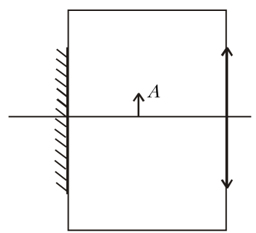
Một thanh kim loại $OM$ chiều dài $l=1\text{,}2\ \text{m}$, đầu O gắn với một trục quay cố định. Thanh quay quanh trục trong một từ trường đều cảm ứng từ $B=0\text{,}5\ \text{T}$ với tốc độ góc $\omega=2\ \text{rad/s}$, trong mặt phẳng vuông góc với các đường sức từ (Hình 2). Xác định hiệu điện thế $U_{OM}$ giữa hai đầu $O$, $M$.
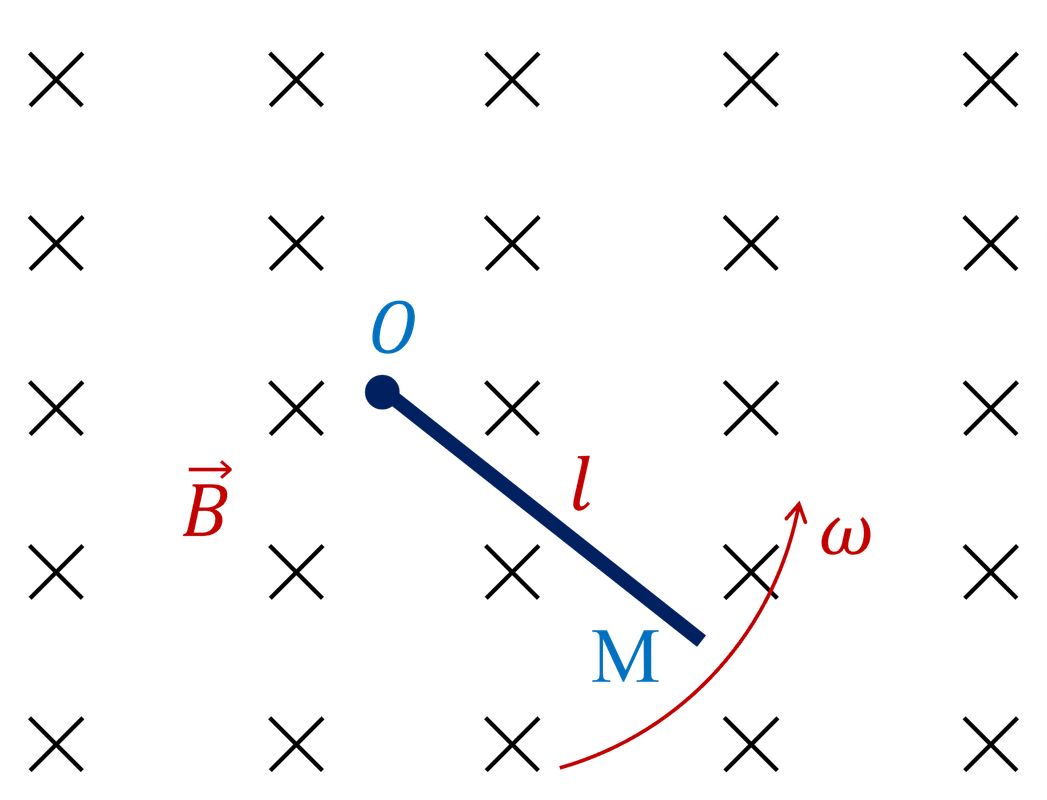
Vì hai đầu thanh để hở nên suất điện động cảm ứng trên thanh bằng hiệu điện thế hai đầu thanh.
Đối với chuyển động quay này của thanh kim loại, nếu ta áp dụng công thức $E_c=Bvl\sin{\alpha}$ thì rất khó, bởi lẽ công thức này chỉ áp dụng được cho chuyển động tịnh tiến của một thanh, ở đó tất cả các điểm trên thanh có cùng vận tốc. Ở đây, vận tốc tăng dần từ $O$ đến $M$ nên muốn áp dụng công thức, ta phải chia nhỏ thanh và lấy tích phân.
Ngược lại, nếu ta áp dụng công thức định luật cảm ứng điện từ của Faraday thì rất đơn giản, độ lớn suất điện động trên thanh là: \begin{align} \left|E_c\right|&=\left|\frac{\Delta\Phi}{\Delta t}\right|\\ &=\left|\frac{B\Delta S}{\Delta t}\right|\\ &=\frac{B\frac{\omega l^2\Delta t}{2}}{\Delta t}\\ &=\frac{B\omega l^2}{2} \end{align}
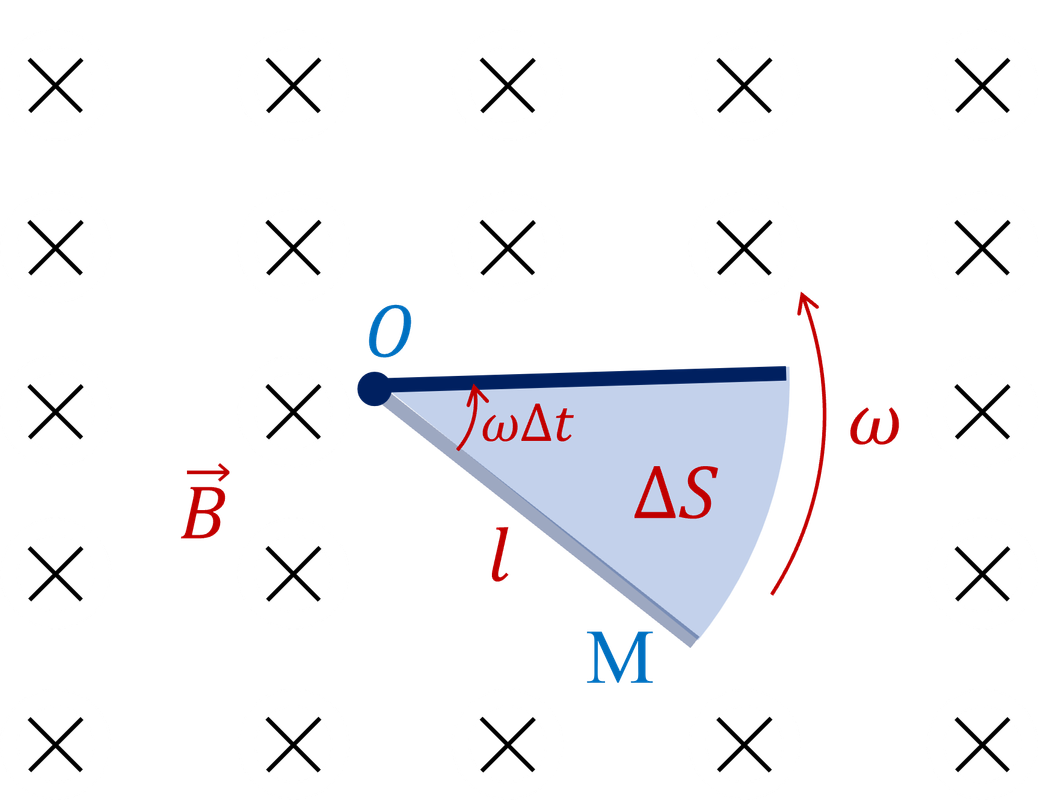
Áp dụng quy tắc bàn tay trái ta suy ra được cực dương của suất điện động cảm ứng ở đầu O, cực âm ở đầu M. Tức là hiệu điện thế \begin{align} U_{OM}=\frac{B\omega l^2}{2}&=\frac{0\text{,}5\times 2\times 1\text{,}2^2}{2}\\ &=0\text{,}72\ \text{V} \end{align}
Bài toán 2. Thanh kim loại quay trong một mặt phẳng trong từ trường với trục quay ở giữa thanh
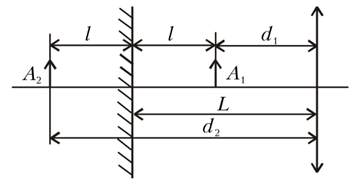
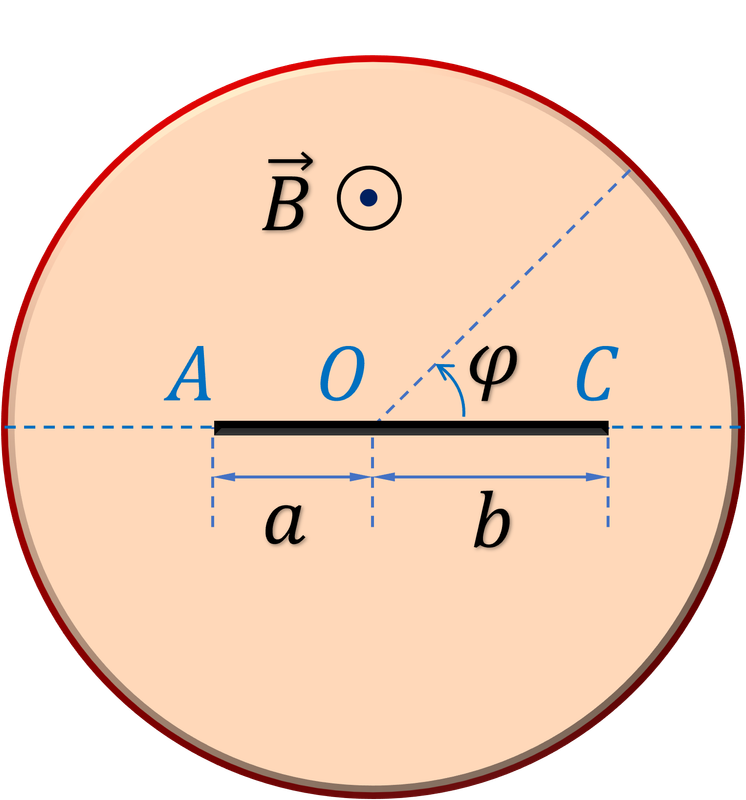
Một thanh dẫn điện mảnh $AC$ được gắn vào một đĩa không dẫn điện nằm ngang dọc theo đường kính của nó. Đĩa đặt trong từ trường đều có cảm ứng $B = 10^{−2}\ \text{T}$, vuông góc với mặt phẳng của đĩa (Hình 3). Chiều dài của thanh $L = a + b$, trong đó $a = 0\text{,}5\ \text{m}$, $b = 1\ \text{m}$.
Đĩa quay quanh trục thẳng đứng đi qua điểm O với tốc độ góc không đổi $ω_0 = 5\ \text{rad/s}$, tính hiệu điện thế giữa hai đầu A, C của thanh.
Đĩa thực hiện dao động quay quanh trục thẳng đứng đi qua điểm O với phương trình $\varphi = \varphi_0 \cos{ωt}$, trong đó $t$ là thời gian.Xác định hiệu điện thế lớn nhất giữa hai đầu thanh $A$ và $C$, nếu $\varphi_0 = 0\text{,}6\ \text{rad}$ và $ω = 0\text{,}2\ \text{rad/s}$.
1. Thanh quay đều với tốc độ góc $\omega_0=5\ \text{rad/s}$
Trên mỗi đoạn $OA$ và $OC$ ta có một hiệu điện thế. Áp dụng kết quả của bài toán 1 (chú ý chiều của từ trường đã được đảo ngược lại nên dấu của hiệu điện thế cũng được thay đổi) ta có \begin{align} U_{AO}=\frac{B\omega_0 a^2}{2}, U_{CO}=\frac{B\omega_0 b^2}{2} \end{align} \begin{align} U_{AC}&=U_{AO}+U_{OC}\\ &=U_{AO}-U_{CO}\\ &=\frac{B\omega_0 a^2}{2}-\frac{B\omega_0 b^2}{2}\\ &=\frac{1}{2}B\omega\left(a^2-b^2\right)\\ &=\frac{1}{2}\times 10^{-2}\times 5\times\left(0\text{,}5^2-1^2\right)\\ &=-0\text{,}01875\ \text{V} \end{align}
2. Thanh dao động điều hòa theo phương trình $\varphi = \varphi_0 \cos{ωt}$
Ở ý 1. góc $\varphi$ biến thiên tuyến tính theo thời gian $t$ nên chúng ta áp dụng công thức $E_c=-\frac{\Delta \Phi}{\Delta t}$, còn bây giờ góc $\varphi$ biến thiên điều hòa, ta phải sử dụng công thức chính xác hơn, đó là $$E_c=-\frac{d\Phi}{dt}$$ Trong đó \begin{align} d\Phi=BdS=\frac{Bl^2}{2}d\varphi \end{align} Như vậy ta có \begin{align} E_c=-\frac{Bl^2}{2}\frac{d\varphi}{dt} \end{align} Với $\varphi = \varphi_0 \cos{ωt}$ thì đạo hàm của nó theo $t$ bằng $$\frac{d\varphi}{dt}=-\omega\varphi_0\sin{\omega t}$$ Bây giờ ta đã có biểu thức tổng quát tính suất điện động cảm ứng trên một phần của thanh $$E_c=\frac{B\omega \varphi_0 l^2}{2}\sin{\omega t}$$ Trên các đoạn $AO$ và $OC$ ta có thể áp dụng tính được các suất điện động $$ E_1=\frac{B\omega \varphi_0 a^2}{2}\sin{\omega t}\\ E_2=\frac{B\omega \varphi_0 b^2}{2}\sin{\omega t} $$ Cũng lập luận như ý 1., ta tính được hiệu điện thế giữa $A$ và $C$ \begin{align} U_{AC}&=E_1-E_2\\ &=\frac{B\omega \varphi_0}{2}\left(a^2-b^2\right)\sin{\omega t} \end{align} Hiệu điện thế cực đại giữa hai điểm này là \begin{align} U_\text{max}&=\left|\frac{B\omega \varphi_0}{2}\left(a^2-b^2\right)\right|\\ &=\left|\frac{10^{-2}\times 0\text{,}2\times 0\text{,}6}{2}\left(0\text{,}5^2-1^2\right)\right|\\ &=4\text{,}5.10^{-4}\ \text{V} \end{align}
Bài toán 3. Thanh kim loại quay tạo thành hình nón trong từ trường
Thanh kim loại $AC$ được gắn bản lề ở một đầu (điểm $A$) với thanh điện môi thẳng đứng $AO$. Đầu kia (điểm $C$) được nối với thanh thẳng đứng bằng sợi dây nằm ngang không dãn, không dẫn điện $OC$ có chiều dài $R = 1\ \text{m}$ (Hình 5). Thanh $AC$ quay quanh trục $AO$ trong một từ trường đều, cảm ứng từ thẳng đứng và có độ lớn $B = 10^{−2}\ \text{T}$. Vận tốc góc quay của thanh $AC$ là $ω = 60\ \text{rad/s}$. Xác định hiệu điện thế giữa hai điểm $A$ và $C$.
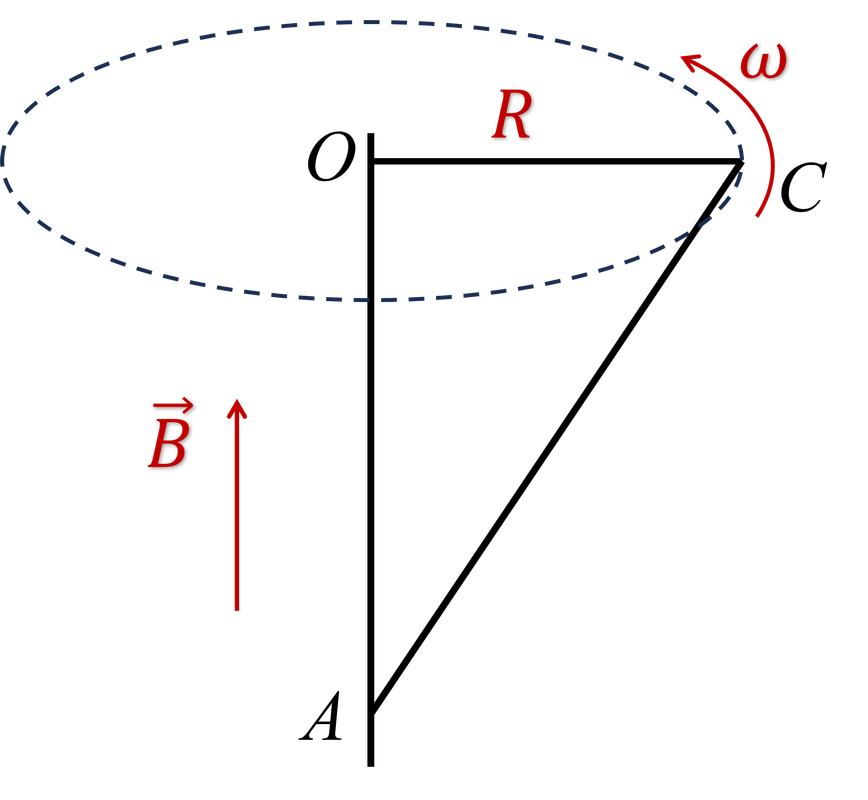
Nếu sử dụng công thức $E_c=Bvl\sin{\alpha}$ ở bài toán này thì việc xác định $v$ càng khó khăn hơn nữa, bởi vì không những thanh quay mà còn quay trong một mặt nón, rất phức tạp. Tuy nhiên, để áp dụng công thức $E_c=-\frac{\Delta \Phi}{\Delta t}$, ta phải lập luận một chút. Đó là, từ thông gửi qua mặt nón cũng chính là từ thông gửi qua mặt đáy của nón, nơi sợi dây $OC$ quét được. Tức là ta có thể áp dụng kết quả của bài toán 1, trong đó $l$ được thay bằng $R$ ở bài toán này. Cụ thể độ lớn suất điện động trên thanh $AC$ bằng \begin{align} \left|E_c\right|&=\left|\frac{B\omega R^2}{2}\right|\\ &=\left|\frac{10^{-2}\times 60\times 1^2 R^2}{2}\right|\\ &=0\text{,}3\ \text{V} \end{align} Áp dụng quy tắc bàn tay trái ta xác định được đầu $C$ là cực dương, tức là \begin{align} U_{AC}=-0\text{,}3\ \text{V} \end{align}
Bài toán 4. Thanh kim loại gấp khúc quay trong từ trường
Trong từ trường đều, trong mặt phẳng vuông góc với vectơ cảm ứng từ $B = 200\ \text{mT}$, một thanh dẫn gấp khúc gồm ba đoạn thẳng giống hệt nhau, hai đoạn kề nhau vuông góc với nhau, quay với vận tốc góc $ω = 1\ \text{rad/s}$ quanh trục đi qua qua điểm O, vuông góc với các đoạn thẳng. Chiều dài mỗi đoạn thẳng là $l = 60\ \text{cm}$. Xác định hiệu điện thế $U_{AD}$ giữa hai điểm $A$ và $D$.
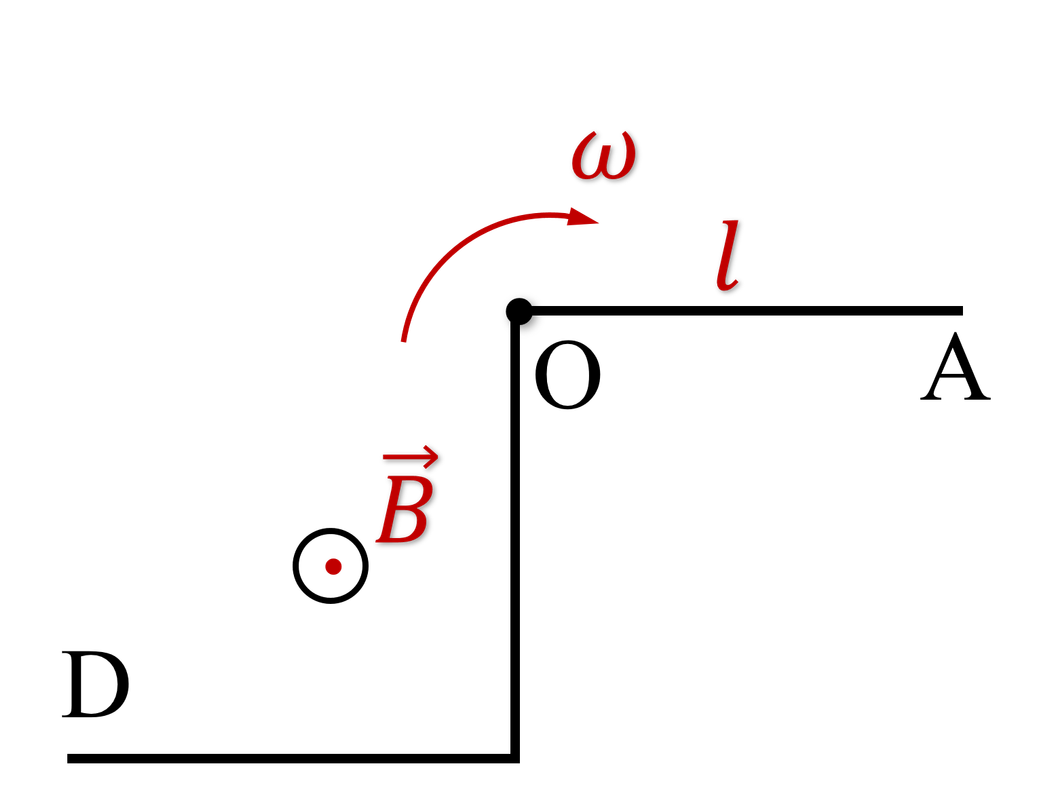
Suất điện động trên đoạn $OA$ có độ lớn (áp dụng kết quả bài toán 1) $$\left|E_1\right|=\frac{B\omega l^2}{2}$$ và đầu $O$ là cực dương, tức là hiệu điện thế $$U_{AO}=-\frac{B\omega l^2}{2}$$ Diện tích mà đoạn gấp khúc $OD$ quét được đúng bằng diện tích mà đoạn thẳng $OD$ quét, tức là suất điện động trên hai phần vuông góc này được xem như suất điện động trên đoạn thẳng $OD=l\sqrt{2}$, có độ lớn bằng $$\left|E_2\right|=\frac{B\omega \left(l\sqrt{2}\right)^2}{2}=B\omega l^2$$ Ở đây đầu $O$ vẫ là cực dương, nên hiệu điện thế $$U_{OD}=B\omega l^2$$ Và cuối cùng \begin{align} U_{AD}&=U_{AO}+U_{OD}\\ &=-\frac{B\omega l^2}{2}+B\omega l^2\\ &=\frac{B\omega l^2}{2}\\ &=\frac{0\text{,}2\times 1\times 0\text{,}6^2}{2}\\ &=0\text{,}036\ \text{V} \end{align}
Bài toán 5. Đĩa kim loại quay trong từ trường
Một đĩa có bán kính $r$, độ dày $h$ được làm bằng kim loại có điện trở suất $\rho$. Đĩa quay quanh trục nằm ngang đi qua tâm của nó với tốc độ góc không đổi $\omega$. Một từ trường đều $B$ không đổi được tạo ra trong một vùng hình tròn diện tích $S$ rất nhỏ trên đĩa, gần mép của nó. Tính công suất tỏa nhiệt trên đĩa.
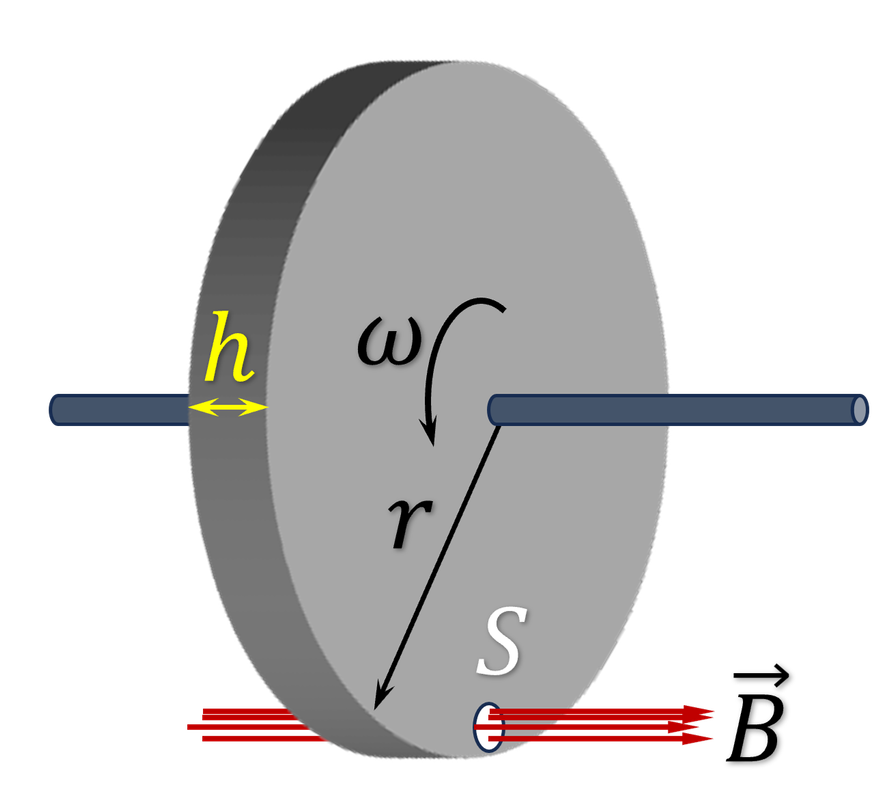
Thoạt nhìn ta thấy rằng chẳng có sự biến thiên từ thông nào trên đĩa cả, tuy nhiên đây là sự chuyển động của một vật dẫn trong từ trường. Trên đĩa sẽ có sự dịch chuyển có hướng của các điện tích tự do vì chịu tác dụng của lực Lorentz, đó là dòng điện cảm ứng và nó tác dụng tỏa nhiệt trên đĩa.
Nếu ta chọn đĩa làm hệ quy chiếu thì trên đĩa có những vùng mà từ trường quét qua, tức là có sự biến thiên từ thông theo thời gian. Vì vùng hình tròn rất nhỏ nên khi tính toán ta xem nó như một hình vuông nhỏ cách trục quay một khoảng $r$ (vì sát mép đĩa). Cạnh của hình vuông là $$a=\sqrt{S}$$ Thời gian mà từ trường quét qua diện tích $S$ là $$\Delta t=\frac{a}{v}=\frac{\sqrt{S}}{\omega r}$$ Suất điện động cảm ứng xuất hiện trên vùng đĩa $S$ trong thời gian này là \begin{align} E_c&=-\frac{\Delta \Phi}{\Delta t}\\ &=-\frac{BS}{\frac{\sqrt{S}}{\omega r}}\\ &=-Br\omega\sqrt{S} \end{align}
Điện trở của vùng đĩa có diện tích $S$ này là \begin{align} R&=\rho\frac{a}{ah}\\ &=\frac{\rho}{h} \end{align}
Công suất tỏa nhiệt trên đĩa chính là công suất tỏa nhiệt trong vùng $S$, nó bằng \begin{align} P&=\frac{E_c^{2}}{R}\\ &=\frac{hSB^2r^2\omega^2}{\rho} \end{align}
Kết luận
Qua một số bài toán về chuyển động của thanh dẫn trong từ trường ở trên ta thấy, việc áp dụng công thức tính suất điện động cảm ứng theo định luật Faraday để tính suất điện động trong thanh dẫn chuyển động quả thực rất hiệu quả. Câu hỏi lại đặt ra một lần nữa: Suất điện động trên một đoạn dây dẫn chuyển động trong từ trường có phải là suất điện động cảm ứng không? Nếu cố gắng giải thích thì câu trả lời có thể là: đúng. Nếu chúng ta quan sát chuyển động của thanh từ bên ngoài thì đại lượng $\Delta \Phi$ chỉ là từ thông gửi qua diện tích mà dây đã quét qua trong thời gian $\Delta t$ (tức là chẳng có độ biến thiên từ thông nào cả). Tuy nhiên nếu đứng trên thanh mà quan sát thì rõ ràng $\Delta \Phi$ chính là độ biến thiên từ thông gửi qua dây dẫn trong thời gian $\Delta t$. Điều này hoàn toàn phù hợp với nội dung định luật Faraday về cảm ứng điện từ.