Câu 1. Mô hình phanh trong tháp rơi tự do
Sự thu hút nổi bật tại nhiều công viên giải trí là tháp rơi tự do. Trong doodle dễ thương mà Google dành cho ngày Valentine và George Ferris (người tạo ra vòng đu quay khổng lồ đầu tiên ở Chicago năm 1893) vào ngày 14 tháng 2, có một trong những tháp này, ở phần bên phải của hình ảnh.
Nguyên nhân "thu hút" này bao gồm việc nâng một bệ lên độ cao $H$, trên bệ là những hành khách đang “chịu đựng đau khổ” ngồi và được buộc chặt. Từ độ cao $H$ này, bệ được thả rơi tự do xuống điểm $\text{B}$, tại đó lực hãm $F$ bắt đầu tác dụng. Đương nhiên, lực này phải khiến bệ dừng hẳn khi chạm đất.
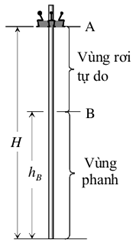
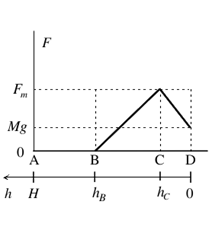
1) Giả sử lực phanh tác dụng giữa điểm B và mặt đất là không đổi (Hình 1).
-
Biết độ cao của điểm $\text{B}$ là $h_{\text{B}}=\dfrac{3H}{5}$, hãy xác định giá trị của lực $F$ theo gia tốc trọng trường $g$ và tổng khối lượng $M$ của sàn và hành.
-
Tốc độ tối đa đạt được tại thời điểm nào trong quá trình hạ xuống? Xác định tốc độ tối đa $v_{\mathrm{max}}$ này theo $g$ và $H$.
2) Với quy trình trước, hành khách sẽ chịu sự thay đổi gia tốc đột ngột khi đi qua điểm $\mathrm{B}$ và khi chạm đất $\mathrm{D}$, điều này rất không tốt cho sức khỏe của họ. Do đó, nên làm trơn tru thời điểm bắt đầu và kết thúc quá trình phanh. Trên thực tế, các quy trình phanh khí nén hoặc cơ điện được sử dụng để đạt được hiệu ứng tương tự như sau: lực phanh tăng tuyến tính giữa các điểm $\mathrm{B}$ và $\mathrm{C}$ trong Hình 2, từ $0$ đến giá trị cực đại $F_{\mathrm{m}}$, và sau đó, giữa $\mathrm{C}$ và $\mathrm{D}$ lực $F$ giảm tuyến tính đến một giá trị bằng trọng lượng $Mg$, như minh họa sơ đồ trong Hình 3. Theo cách này, gia tốc cuối cùng cũng bằng $0$, và quá trình "hạ cánh" không bị giật mạnh.
- Xác định giá trị $F_{\mathrm{m}}$ sao cho bệ đáp xuống đất với vận tốc bằng $0$. Biểu thị kết quả theo $M$ và $g$, lưu ý rằng $h_{\mathrm{B}}=\dfrac{3H}{5}$ và $h_{\mathrm{C}}=\dfrac{H}{5}$.
- Tại thời điểm nào trong quá trình hạ xuống, bệ đạt tốc độ cực đại? Xác định tốc độ tối đa $v_{\mathrm{max}}$ này theo $g$ và $H$.
- Tính tốc độ tối đa cho một tòa tháp có chiều cao $H=100\ \mathrm{m}$.
Câu 2. Giác quan thứ sáu của cá mập
Cá mập sở hữu các cơ quan cảm giác đặc biệt, gọi là ống Lorenzini, cho phép chúng phát hiện điện trường yếu được tạo ra bởi sự phân bố lại điện tích trong cơ thể con mồi, do sự co cơ gây ra. Sự phân bố lại điện tích này tuân theo mô hình đơn giản của một lưỡng cực điện: hai điện tích bằng nhau, trái dấu, $+Q$ và $-Q$, cách nhau một khoảng $L$ (Hình 1).
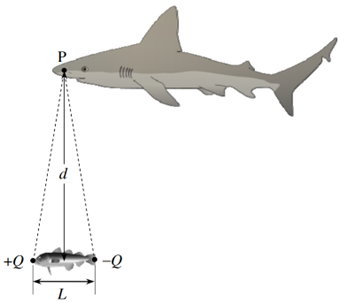
1) Xác định cường độ điện trường do cá (lưỡng cực) tạo ra tại điểm $\mathrm{P}$, cách tâm của nó một khoảng $d$ và vuông góc với đường thẳng nối các điện tích, như thể hiện trong Hình 4. Biểu thị kết quả theo $Q$, $L$, $d$ và hằng số Coulomb $k$.
Như bạn đã biết, trường tĩnh điện do một điện tích điểm tạo ra giảm theo bình phương khoảng cách, nhưng trường do một lưỡng cực tạo ra lại có tính chất khác.
2) Ở khoảng cách lớn từ lưỡng cực, tức là khi $d>>L$, thì cường độ điện trường thu được trong phần trước giảm như thế nào theo $d$?
Hướng dẫn: Vì $L$ rất nhỏ so với $d$ nên chúng ta có thể lấy $\left(\frac{L}{d}\right)^2\approx0$.
Cá mập có thể định vị một con cá cách xa vài mét, vì cường độ điện trường tối thiểu mà chúng có thể phát hiện rất thấp, $E_{\mathrm{min}}=0{,}5\ \mathrm{\mu V\!/\!m}$.
3) Tính giá trị điện tích Q nếu cá mập có thể phát hiện một con cá có chiều dài $L=20\ \mathrm{cm}$ ở khoảng cách tối đa $d_{\mathrm{max}}=20\ \mathrm{m}$. Cho: hằng số Coulomb trong nước $k=1{,}3\!\cdot\!10^8\ \mathrm{N\!\cdot\! m^2/C^2}$.
Bây giờ chúng ta giả sử rằng con cá mập tiến lại gần một con cá theo hướng của đường thẳng nối các điện tích (hình 2).
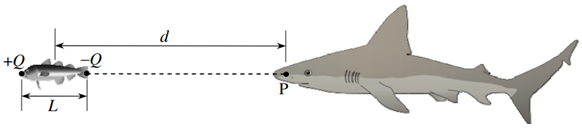
4) Xác định cường độ điện trường tại điểm $\text{P}$, cách tâm lưỡng cực một khoảng $d$.
5) Xấp xỉ kết quả ở ý 4) của bạn đối với khoảng cách rất lớn, tức là $d>>L$.
6) Cá mập sẽ phát hiện ra con cá ở khoảng cách tối đa bằng bao nhiêu?
Câu 3. Dao động điều hòa của con lắc lò xo
Hai vật có khối lượng $m=180\ \mathrm{g}$ và $2m$ nằm trên một mặt bàn nằm ngang nhẵn, được nối với nhau bằng một sợi dây nhẹ không dãn, vật có khối lượng $2m$ được nối với một bức tường thẳng đứng qua một lò xo nhẹ nằm ngang, độ cứng $k=40\ \mathrm{N/m}$. Khi các vật đang đứng yên, sợi dây nối hai vật căng, tác dụng lên vật khối lượng $m$ một lực $\vec{F}$ dọc theo dây nối và trục lò xo, hướng và độ lớn $F=6\ \mathrm{N}$ không đổi. Lấy $\pi^2\approx10$.
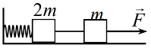
1) Tính gia tốc $a_0$ của các vật tại thời điểm bắt đầu tác dụng lực $\vec{F}$ và gia tốc $a_1$ của các vật tại thời điểm lò xo dãn $3\ \mathrm{cm}$.
2) Tính vận tốc các vật khi lò xo dãn $3\ \mathrm{cm}$.
2) Khi lò xo dãn $3\ \mathrm{cm}$ thì dây nối hai vật bị đứt, tính khoảng cách giữa hai vật sau thời gian $t=0{,}5\ \mathrm{s}$.
Câu 4. Thí nghiệm Young về giao thoa ánh sáng
Trong thí nghiệm Young về giao thoa ánh sáng, hai khe hẹp cách nhau $a=0{,}6\ \mathrm{mm}$ và cách màn quan sát $D=1{,}2\ \mathrm{m}$. Chiếu sáng các khe bằng ánh sáng đơn sắc có bước sóng $\lambda$ ($380\ \mathrm{nm}\le\lambda\le760\ \mathrm{nm}$).
1) Xét trường hợp $\lambda=550\ \mathrm{nm}$.
-
Tính khoảng cách giữa vân sáng bậc 5 và vân tối thứ 3 tính từ vân sáng trung tâm, ở cùng phía so với vân sáng trung tâm.
-
Hai điểm $\text{M}$, $\text{N}$ trên màn, ở hai bên so với vâ sáng trung tâm, cách vân sáng trung tâm lần lượt $2{,}0\ \mathrm{mm}$ và $5{,}6\ \mathrm{mm}$. Tính số vân sáng giữa hai điểm $\text{M}$, $\text{N}$.
2) Tìm $\lambda$ để tại điểm $\text{P}$ trên màn cách vân trung tâm $2{,}4\ \mathrm{mm}$ có vân tối giao thoa.
Câu 5. Tấm làm mát
Một bạn học sinh chơi bóng rổ và môn thể thao này gây áp lực lớn lên các khớp chân, đặc biệt là ở những người trẻ tuổi vẫn đang phát triển. Sau một buổi tập nặng, bạn đặt các túi gel làm lạnh lên các khớp để làm mát. Các túi này chứa gel vẫn mềm dẻo ngay cả khi được làm lạnh xuống nhiệt độ thấp và không chuyển sang thể khác. Bạn học sinh muốn xác định nhiệt dung của túi gel vì cho rằng hiệu quả làm lạnh phụ thuộc vào đại lượng này. Ở nhà, bạn cân túi gel và xác định được khối lượng $m_{ch}=250\ \mathrm{g}$, rồi đặt nó vào tủ đông trong 2 giờ ở nhiệt độ $t_{ch}=-20\ ^\circ\mathrm{C}$. Sau đó bạn chuẩn bị một bình giữ nhiệt miệng rộng và rót vào đó nước có cùng khối lượng $m_v=m_{ch}$, để bình và nước ổn định ở nhiệt độ $t_v=20\ ^\circ\mathrm{C}$. Khi túi gel đã được làm lạnh, bạn bỏ túi vào bình giữ nhiệt, đậy kín và chờ đến khi nhiệt độ túi và nước cân bằng. Khi mở bình thấy túi được bao bọc bởi lớp băng; bạn lấy túi cùng lớp băng ra, nhanh lau khô bằng khăn giấy và cân lại, được khối lượng túi kèm băng là $m_{ch}^\prime=390\ \mathrm{g}$. Bỏ qua nhiệt dung của bình giữ nhiệt và ảnh hưởng của vỏ mỏng túi.
Cho số liệu: nhiệt dung riêng của nước $c_v=4{,}2\ \mathrm{J/(g·K)}$ và nhiệt nóng chảy riêng của nước $\lambda_v=334\ \mathrm{J/g}$.
1) Tìm nhiệt độ cân bằng cuối cùng.
2) Tính nhiệt lượng $Q$ mà túi gel nhận được.
3) Tính nhiệt dung $C_{ch}$ của túi gel và nhiệt dung riêng $c_{ch}$ của gel.
