Chuyển động của các thiên thể trong trường hấp dẫn

Chuyển động của các thiên thể trong trường hấp dẫn là một mảng kiến thức cốt lõi của cơ học thiên thể và cũng là chủ đề “ăn điểm” trong các chuyên đề ôn thi Học sinh giỏi Vật lí. Những năm gần đây, đề thi HSG Quốc gia môn Vật lí thường xuyên xuất hiện các câu hỏi về chuyển động trong trường hấp dẫn (vệ tinh, hành tinh, tàu vũ trụ), yêu cầu học sinh nắm vững định luật vạn vật hấp dẫn, vận dụng thành thạo các định luật động lực học và suy ra các hệ quả kinh điển như các định luật Kepler. Bài viết này được biên tập theo hướng chuyên đề bồi dưỡng học sinh giỏi Vật lí: hệ thống hoá các tích phân chuyển động (bảo toàn mômen động lượng, “tích phân diện tích”/Kepler II và tích phân năng lượng), đồng thời tổng hợp chuỗi bài toán chọn lọc về quỹ đạo elip–hypebol, rơi vệ tinh, chuyển quỹ đạo và bay sượt hấp dẫn (gravity assist). Nội dung phù hợp để giáo viên dùng khi ra đề – chữa đề, và giúp học sinh rèn kĩ năng biến đổi nhanh cho các kì thi HSG Quốc gia, khu vực, Quốc tế và Olympic Vật lí.

Bài viết được trình bày theo mục lục sau đây:

• I. Kiến thức trọng tâm về chuyển động của các thiên thể trong trường hấp dẫn
  • 1. Trường xuyên tâm & mômen động lượng (Kepler II)
  • 2. Tích phân năng lượng & vận tốc quỹ đạo
  • 3. Cận tâm – viễn tâm, Viète, bán trục lớn
  • 4. Kepler III và hệ hai vật
  • 5. Quỹ đạo elip/hypebol và tham số $a,e,p,b$
• II. Hệ thống bài toán về chuyển động của các thiên thể trong trường hấp dẫn
  • Bài toán 1. Dòng hạt bụi vũ trụ – bắt giữ hấp dẫn
  • Bài toán 2. Vệ tinh hãm tốc – thời gian rơi
  • Bài toán 3. Mô-đun rơi xuống Mặt Trăng – vận tốc tách
  • Bài toán 4. Năng lượng tối thiểu để thoát trường hấp dẫn
  • Bài toán 5. Chuyển quỹ đạo Trái Đất → Sao Thổ (Hohmann)
  • Bài toán 6. Quỹ đạo cận nhật $0.01$ AU – góc bẻ & vận tốc phóng
  • Bài toán 7. Bay sượt hành tinh – $r_{\min}$ và góc lệch $\varphi$
  • Bài toán 8. Vượt vận tốc cấp ba – $v_k$ và góc tiệm cận $\alpha$
  • Bài toán 9. Gravity assist Sao Hỏa – độ lệch tâm & năng lượng pin
• III. Bài tập tự giải

I. Kiến thức trọng tâm về chuyển động của các thiên thể trong trường hấp dẫn

1. Trường lực xuyên tâm và bảo toàn mômen động lượng (tích phân diện tích – Kepler II)

Ta xét một vài khái quát và hệ quả then chốt làm nền tảng cho mô tả chuyển động trong trường lực trung tâm. Khi hai vật tương tác hấp dẫn, tâm khối của chúng được coi là tâm hút và gắn với nó một “cực”, tức gốc của vectơ bán kính mô tả chuyển động. Khi khối lượng hai vật chênh lệch nhau nhiều bậc, người ta coi tâm hút là tâm khối của vật lớn, và hệ quy chiếu gắn với nó là quán tính. Lực hấp dẫn tác dụng lên vật thứ hai và vectơ bán kính mô tả chuyển động của nó là hai vectơ cùng phương. Tích có hướng của chúng (mômen lực) bằng không. Theo phương trình động lực học quay, mômen động lượng của vật thứ hai đối với tâm hút là đại lượng bảo toàn:

$$\begin{align} \vec{M} &= \vec{r}\times\vec{F}=0,\\ \vec{M} &= \frac{d\vec{L}}{dt}=0. \end{align}$$

$$\begin{align} \vec{L} &= \vec{r}\times m\vec{v}=\text{const},\\ \vec{r}\times\vec{v} &= \text{const}. \end{align}$$

Người ta gọi $\vec{r}\times\vec{v}=\vec{s}_0$ là tốc độ quét diện tích (tốc độ “sector”), trong đó $s_0=2S_t$, với $S_t$ là diện tích mà vectơ bán kính quét được trong mỗi giây đối với một vật chuyển động trong trường lực trung tâm. Tính không đổi của $s_0$ chính là nội dung của định luật Kepler thứ hai. Cách suy luận trên được gọi là tích phân diện tích. Thực chất, nó biểu diễn định luật bảo toàn mômen động lượng, vì $L=2mS_t$.

Nếu đưa vào tham số ngắm (tham số va chạm) $b=r\sin\alpha$, tức độ dài đoạn vuông góc kẻ từ tâm hút đến phương của vectơ xung lượng, thì kết quả của ta ở dạng vô hướng cho hai điểm trên quỹ đạo sẽ là:

$$\begin{align} v_0b_0 &= v_1b_1 = 2S_t = \text{const}. \end{align}$$

2. Tích phân năng lượng và hệ thức vận tốc trên quỹ đạo

Tính bảo toàn (trường thế) của trường hấp dẫn cho phép đưa vào đặc trưng năng lượng của trường và thêm một tích phân chuyển động nữa — tích phân năng lượng. Ta nhân từng vế phương trình động lực học cơ bản cho trường hấp dẫn $m\dfrac{dv}{dt}=\dfrac{GMm}{r^2}$ với $v=\dfrac{dr}{dt}$ và biến đổi. Kết quả thu được:

$$\begin{align} \frac{d}{dt}\left(\frac{v^2}{2}-\frac{GM}{r}\right) &= 0,\\ \frac{v^2}{2}-\frac{GM}{r} &= E_0=\text{const}. \end{align}$$

Số hạng thứ hai biểu thị thế năng của một đơn vị khối lượng trong trường hấp dẫn, tức thế hấp dẫn, còn toàn bộ biểu thức là định luật bảo toàn năng lượng. Ở dạng quen thuộc, cho hai điểm trên quỹ đạo có thể viết:

$$\frac{mv_1^2}{2}-\frac{GMm}{r_1}=\frac{mv_2^2}{2}-\frac{GMm}{r_2}.$$

Năng lượng toàn phần của một đơn vị khối lượng quyết định dạng quỹ đạo. Với quỹ đạo elip có bán trục lớn $a$, ta có:

$$E_0=-\frac{GM}{2a}.$$

Khi đó tích phân năng lượng nhận dạng:

$$v^2=GM\left(\frac{2}{r}-\frac{1}{a}\right).$$

3. Cận tâm – viễn tâm, hệ thức Viète và ý nghĩa bán trục lớn

Hệ thức ngay trên đây liên hệ vận tốc của vật tại khoảng cách $r$ đến tâm hút với bán trục lớn $a$ của quỹ đạo và được dùng rất rộng rãi khi tính toán quỹ đạo. Ở đây đã nêu cách chứng minh năng lượng toàn phần của một đơn vị khối lượng trên quỹ đạo elip, sử dụng cả hai tích phân chuyển động. Tích phân diện tích sẽ được viết cho các điểm cận tâm tại cận tâm và viễn tâm, khi vận tốc vuông góc với vectơ bán kính:

$$\begin{align} v_1r_1 &= v_2r_2 = S,\\ v &= \frac{S}{r}. \end{align}$$

$$\frac{v^2}{2}-\frac{GM}{r}=E_0,\qquad r^2+\frac{GM}{E_0}\,r-\frac{S^2}{2E_0}=0.$$

Hai nghiệm của phương trình sau cùng tương ứng với khoảng cách đến viễn tâm và cận tâm $r_1$ và $r_2$. Tổng các khoảng cách này:

$$r_1+r_2=2a,$$

trong đó $a$ là bán trục lớn của quỹ đạo. Nhưng theo định lý Viète, $r_1+r_2=-\dfrac{GM}{E_0}$. Do đó

$$E_0=-\frac{GM}{2a}$$

là năng lượng cơ học toàn phần của một đơn vị khối lượng trong trường hấp dẫn đối với quỹ đạo elip.

4. Định luật Kepler III và dạng tổng quát cho hệ hai vật

Phương trình động lực học cơ bản và định luật vạn vật hấp dẫn cũng suy ra định luật Kepler thứ ba. Với quỹ đạo tròn, việc này khá đơn giản. Thật vậy,

$$\begin{align} m\,a_{\text{ht}} &= \frac{GMm}{r^2},\\ a_{\text{ht}} &= \frac{4\pi^2 r}{T^2},\\ \frac{T^2}{r^3} &= \frac{4\pi^2}{GM}. \end{align}$$

Vì $M$ là khối lượng Mặt Trời nên với mọi hành tinh, vế trái của đẳng thức cuối là như nhau. Việc xét chuyển động của hệ hấp dẫn quanh tâm khối cho phép Newton hiệu chỉnh. Dạng tổng quát cho quỹ đạo elip là

$$\frac{T^2}{a^3}\,(m_1+m_2)=\frac{4\pi^2}{G}.$$

Tỉ số giữa bình phương chu kỳ quỹ đạo của hai vật và lập phương khoảng cách trung bình giữa chúng, nhân với tổng khối lượng hai vật, là một hằng số. Hệ thức này cho phép xác định tổng khối lượng của các vật quay quanh nhau, ví dụ các sao đôi hoặc hành tinh có vệ tinh.

5. Phương trình quỹ đạo thiết diện cônic (elip/hypebol) và các tham số $a,e,p,b$

Tùy theo năng lượng toàn phần, vật chuyển động trong trường lực trung tâm theo quỹ đạo elip, parabol hoặc hypebol. Các quỹ đạo như vậy (gọi là các đường cong bậc hai) được mô tả bởi phương trình của các thiết diện cônic. Ta viết phương trình elip trong toạ độ cực với cực tại tiêu điểm của đường cong:

$$r(\varphi)=\frac{p}{1+e\cos\varphi}.$$

Ở đây $p$ là tham số, $e$ là độ lệch tâm (eccentricity) của elip, $\varphi$ là dị thường thật, tức góc tại tiêu điểm giữa hướng đến cận điểm (cận tâm) và hướng đến vị trí của chất điểm.

Làm rõ ý nghĩa của tham số: với $\varphi=\dfrac{\pi}{2}$ thì $r=p$. Nếu $\varphi=0$ thì $p=r_p(1+e)$, còn nếu $\varphi=\pi$ thì $p=r_a(1-e)$. Vì thế

$$r_p+r_a=2a,\qquad p=a(1-e^2),$$

và phương trình elip có dạng

$$r(\varphi)=a\,\frac{1-e^2}{1+e\cos\varphi}.$$

Hình 1

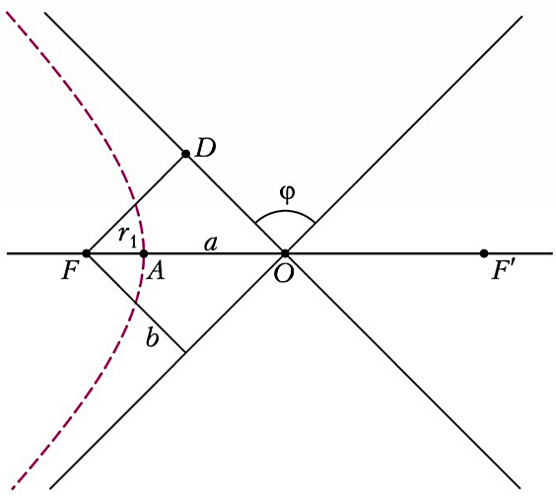
Vì khoảng cách từ tâm elip đến tiêu điểm (xem Hình 1) là $OF=ea$, nên bán trục nhỏ $b=a\sqrt{1-e^2}$. Diện tích elip $S=\pi ab$, hay $S=\pi a^2\sqrt{1-e^2}$. Từ diện tích và chu kỳ có thể biểu diễn tốc độ quét diện tích.

Một số tính chất và đặc trưng của quỹ đạo hypebol sẽ được xét khi phân tích các bài toán cụ thể.

II. Hệ thống các bài toán về chuyển động của các thiên thể trong trường hấp dẫn

Bài toán 1. Chuyển động của dòng các hạt bụi trong trường hấp dẫn của Trái Đất

Dòng các hạt bụi vũ trụ có nồng độ $n$ và khối lượng trung bình $m_0$ chuyển động về phía Trái Đất, với vận tốc tương đối $v_0$ ở khoảng cách rất lớn so với Trái Đất. Trong thời gian $t$, khối lượng bụi vũ trụ nào rơi xuống Trái Đất?

Nếu biết tham số ngắm $r_0$ ứng với trường hợp bắt giữ hấp dẫn các hạt, thì khối lượng vật chất bị bắt giữ được xác định bởi thể tích một hình trụ có bán kính đáy $r_0$ và mật độ bụi $\rho=m_0n$:

$$\Delta m=m_0n\,\pi r_0^2 v_0 t.$$

Tham số ngắm $r_0$ được xác định bởi khoảng cách lớn nhất của các hạt đến trục dòng, sao cho lực hút của trường hấp dẫn còn đủ để…thì hạt sẽ chạm bề mặt Trái Đất tại điểm cận tâm, nơi $r_1=R_\oplus$ (ở đây $\vec{R}_\oplus \perp \vec{v}_1$). Viết tích phân diện tích và định luật bảo toàn năng lượng cho hai trạng thái:

$$\begin{align} r_0v_0 &= R_\oplus v_1,\\ \frac{m_0v_0^2}{2} &= \frac{m_0v_1^2}{2}-\frac{GMm_0}{R_\oplus}. \end{align}$$

Lưu ý rằng $\dfrac{GM}{R_\oplus^2}=g_0$. Do đó $v_1^2=v_0^2+2g_0R_\oplus$ và tham số ngắm

$$r_0=R_\oplus\sqrt{1+\frac{2g_0R_\oplus}{v_0^2}},$$

suy ra khối lượng vật chất rơi xuống Trái Đất:

$$\Delta m=m_0n\,\pi R_\oplus^2\left(1+\frac{2g_0R_\oplus}{v_0^2}\right)v_0t.$$

Bài toán 2. Vệ tinh bị hãm tốc: thời gian rơi từ quỹ đạo tròn sang quỹ đạo elip chạm hành tinh

Một vệ tinh đang chuyển động trên quỹ đạo tròn bán kính $R_c$ bị hãm tốc và chuyển sang quỹ đạo elip, tiếp xúc bề mặt hành tinh bán kính $R_p$ tại cận điểm. Hãy xác định thời gian vệ tinh rơi xuống hành tinh. Khối lượng hành tinh là $M$.

Quỹ đạo mới của vệ tinh là một elip có bán trục lớn $a=\dfrac{R_c+R_p}{2}$, và thời gian rơi bằng nửa chu kỳ, tức $\tau=\dfrac{T}{2}$. Chu kỳ chuyển động trên elip thỏa

$$T^2=\frac{4\pi^2}{GM}\,a^3.$$

Suy ra thời gian rơi theo bán trục lớn của quỹ đạo:

$$\tau=\frac{\pi}{2}\,(R_c+R_p)\sqrt{\frac{R_c+R_p}{2GM}}.$$

Bài toán 3. Tách mô-đun khỏi vệ tinh Mặt Trăng: vận tốc tương đối để rơi theo quỹ đạo bán elip

Vệ tinh Mặt Trăng chuyển động trên quỹ đạo tròn bán kính $R=3{,}4\cdot10^6\,\text{m}$. Từ vệ tinh tách ra một mô-đun, mô-đun này rơi xuống bề mặt Mặt Trăng theo quỹ đạo bán elip. Hỏi tại thời điểm tách ra, mô-đun phải có vận tốc tương đối so với vệ tinh bằng bao nhiêu? Bán kính Mặt Trăng $R_{\text{L}}=1{,}7\cdot10^6\,\text{m}$, và gia tốc rơi tự do trên bề mặt Mặt Trăng nhỏ hơn 6 lần so với trên bề mặt Trái Đất.

Mô-đun xuất phát từ viễn điểm của quỹ đạo elip, với bán trục lớn $$a=\frac{1}{2}(R+R_{\text{L}})=\frac{3}{2}R_{\text{L}}.$$

Vận tốc (độ lớn) tại viễn điểm tìm từ tích phân năng lượng:

$$v_1=\sqrt{\frac{GM}{R}}\;\sqrt{2-\frac{R}{a}},$$

còn vận tốc tròn của vệ tinh:

$$v_c=\sqrt{\frac{GM}{R}}.$$

Vận tốc tương đối (độ lớn) được xác định bởi hiệu các vận tốc:

$$v_{\text{tđ}}=v_c\left(1-\sqrt{2-\frac{R}{a}}\right).$$

Vì gia tốc rơi tự do trên bề mặt Mặt Trăng $g_0=\dfrac{GM}{R_{\text{L}}^2}$, nên

$$\begin{align} v_c &= \sqrt{\frac{GM}{R}}=\sqrt{\frac{g_0}{R}}\,R_{\text{L}},\\ v_{\text{tđ}} &= \sqrt{\frac{g_0}{R}}\,R_{\text{L}}\left(1-\sqrt{2-\frac{4}{3}}\right) =212\,\text{m/s}, \end{align}$$

và hướng của $\vec{v}_{\text{tđ}}$ ngược chiều với vận tốc quỹ đạo.

Bài toán 4. Năng lượng tối thiểu để tàu thăm dò thoát khỏi trường hấp dẫn hành tinh (từ quỹ đạo elip)

Một tàu thăm dò vũ trụ khối lượng $m$ chuyển động quanh hành tinh khối lượng $M$ theo quỹ đạo có khoảng cách lớn nhất đến tâm hành tinh là $r_a$ và nhỏ nhất là $r_p$. Cần truyền cho tàu thăm dò năng lượng tối thiểu bao nhiêu để nó rời khỏi hành tinh?

Trường hấp dẫn là trường thế. Năng lượng cơ học toàn phần của vật khi chuyển động là hằng số và âm đối với quỹ đạo elip. Để thoát khỏi trường hấp dẫn của hành tinh, cần làm cho năng lượng cơ học toàn phần trở thành không âm. Tích phân năng lượng cho quỹ đạo ban đầu có dạng

$$v_r^2=GM\left(\frac{2}{r}-\frac{1}{a}\right),\qquad a=\frac{r_a+r_p}{2}.$$

Từ đó suy ra

$$\frac{mv_r^2}{2}-\frac{GMm}{r}=-\frac{GMm}{2a}.$$

Đây là biểu thức cho năng lượng toàn phần của vệ tinh. Độ tăng tối thiểu cần thiết của chỉ cần tăng năng lượng cơ học toàn phần của vệ tinh lên bằng không, tức là

$$\Delta E_{\min}-\frac{GMm}{2a}=0,$$

từ đó

$$\Delta E_{\min}=\frac{GMm}{2a},\qquad \Delta E_{\min}=\frac{GMm}{r_a+r_p}.$$

Bài toán 5. Chuyển quỹ đạo Trái Đất → Sao Thổ (Hohmann): tính $\Delta v_1$, $\Delta v_2$, thời gian bay và góc phóng

Cần chuyển một tàu vũ trụ từ quỹ đạo gần Trái Đất sang quỹ đạo tròn gần với quỹ đạo của Sao Thổ, theo quỹ đạo bán elip. Việc này đạt được nhờ một lần đổi vận tốc ban đầu $\Delta v_1$ gần quỹ đạo Trái Đất, rồi một lần đổi vận tốc thứ hai $\Delta v_2$ gần quỹ đạo Sao Thổ. Các lần đổi này là do thay đổi xung lượng tức thời, bỏ qua sự thay đổi khối lượng của tàu. Hãy xác định:
1) Vận tốc chuyển động của Trái Đất và Sao Thổ trên các quỹ đạo tròn bán kính tương ứng $r_3=150\cdot10^6\,\text{km}$ và $r_C=1350\cdot10^6\,\text{km}$. Khối lượng Mặt Trời $M=2\cdot10^{30}\,\text{kg}$.
2) Độ biến thiên vận tốc $\Delta v_1$ để chuyển từ quỹ đạo tròn của Trái Đất sang quỹ đạo bán elip.
3) Độ biến thiên vận tốc $\Delta v_2$ cần thiết để chuyển từ quỹ đạo elip sang quỹ đạo tròn của Sao Thổ.
4) Khoảng cách góc giữa Trái Đất và Sao Thổ tại thời điểm phóng, với điều kiện tàu tiếp cận Sao Thổ tại điểm viễn nhật của quỹ đạo.

Vận tốc nhật tâm của Trái Đất và Sao Thổ:

$$\begin{align} v_{r_3} &= \sqrt{\frac{GM}{r_3}}=29{,}78\cdot10^3\,\text{m/s},\\ v_{r_C} &= \sqrt{\frac{GM}{r_C}}=9{,}93\cdot10^3\,\text{m/s}. \end{align}$$

Bán trục lớn của quỹ đạo chuyển tiếp:

$$a=\frac{r_C+r_3}{2}=7{,}5\cdot10^8\,\text{km}.$$

Vận tốc nhật tâm của tàu tại cận nhật (trên quỹ đạo elip) sau khi ra khỏi vùng ảnh hưởng hấp dẫn của Trái Đất (từ tích phân năng lượng):

$$\begin{align} v_{r_1} &= \sqrt{GM\!\left(\frac{2}{r_3}-\frac{1}{a}\right)} = \sqrt{\frac{GM}{r_3}}\;\sqrt{2-\frac{r_3}{a}} = 1{,}342\,v_{r_3}. \end{align}$$

Do đó độ tăng vận tốc thứ nhất nhỏ hơn:

$$\Delta v_1=v_{r_3}(1{,}342-1)=10{,}18\,\text{km/s}.$$

Tương tự, vận tốc tại viễn nhật ($r_2=r_C$):

$$\begin{align} v_{r_2} &= \sqrt{\frac{GM}{r_2}}\;\sqrt{2-\frac{r_C}{a}} = \sqrt{2-\frac{13{,}5}{7{,}5}}\;\cdot 9{,}93\,\text{km/s} = 4{,}44\,\text{km/s}. \end{align}$$

Độ tăng vận tốc để đưa tàu vào quỹ đạo tròn gần Sao Thổ:

$$\Delta v_2=v_{r_C}-v_{r_2}=5{,}49\cdot10^3\,\text{m/s}.$$

Thời gian bay $\tau$ theo quỹ đạo bán elip bằng nửa chu kỳ. Theo định luật Kepler,

$$\left(\frac{T_a}{T_3}\right)^2=\left(\frac{a}{r_3}\right)^3,\qquad \tau=\frac{T_a}{2}=\frac{T_3}{2}\sqrt{\left(\frac{a}{r_3}\right)^3}\approx 5{,}59\,\text{năm}.$$

Gọi $\varphi_{3C}$ là góc giữa Trái Đất và Sao Thổ tại thời điểm xuất phát, còn $\Delta\varphi_C$ là góc quay của bán kính vectơ Sao Thổ quanh Mặt Trời trong thời gian bay. Vì quỹ đạo chuyển tiếp là bán elip nên góc quét tương ứng bằng $\pi$. Do đó

$$\varphi_{3C}+\Delta\varphi_C=\pi,\qquad \frac{2\pi}{T_C}=\frac{\Delta\varphi_C}{\tau},\qquad \Delta\varphi_C=2\pi\frac{\tau}{T_C},$$

trong đó $T_C=29{,}46\,\text{năm}$ là chu kỳ quỹ đạo của Sao Thổ. Suy ra

$$\varphi_{3C}=\pi\left(1-\frac{2\tau}{T_C}\right) =\pi\left(1-\frac{11{,}18}{29{,}46}\right) =0{,}62\pi \approx 111{,}7^\circ.$$

Bài toán 6. Phóng tàu vào quỹ đạo quanh Mặt Trời có cận nhật $0.01$ AU: góc bẻ vận tốc và vận tốc phóng

Cần đưa một tàu vũ trụ lên quỹ đạo quanh Mặt Trời có cận nhật bằng $0{,}01$ bán kính quỹ đạo Trái Đất, và chu kỳ bằng chu kỳ Trái Đất quay quanh Mặt Trời. Cần phóng tàu từ Trái Đất với vận tốc bao nhiêu và theo hướng nào so với bán kính vectơ Mặt Trời–Trái Đất? Vận tốc quỹ đạo của Trái Đất $v_1=30\,\text{km/s}$.

Bán trục lớn của quỹ đạo tàu phải bằng bán kính quỹ đạo Trái Đất, vì chu kỳ của nó phải bằng chu kỳ Trái Đất (hệ quả của định luật Kepler thứ ba). Khi đó từ tích phân năng lượng suy ra vận tốc nhật tâm của tàu phải bằng vận tốc quỹ đạo của Trái Đất. Có thể đạt quỹ đạo elip yêu cầu bằng cách đổi hướng của vận tốc khi tàu đi ra khỏi vùng ảnh hưởng hấp dẫn của Trái Đất so với vectơ bán kính Mặt Trời – Trái Đất. Để ước lượng góc cần thiết khi đi ra quỹ đạo nhật tâm, ta đặt bằng mômen động lượng của tàu tại điểm “thoát” và tại cận nhật; đồng thời biểu diễn vận tốc ở cận nhật từ tích phân năng lượng:

$$\begin{align} rmv_1\sin\alpha &= r_pmv_p\sin90^\circ = r_pmv_p. \end{align}$$

$$\begin{align} v_p &= \sqrt{\frac{GM}{r}\left(\frac{2}{0.01}-1\right)} = v_1\sqrt{199},\\ \sin\alpha &= \frac{r_pv_p}{rv_1}=0.14,\qquad \alpha=8^\circ. \end{align}$$

Đây là góc giữa các hướng $\vec r_1$ và $\vec v_1$, tức là cần “bẻ” vectơ vận tốc quỹ đạo một góc $\varphi=90^\circ-\alpha=82^\circ$.

Vận tốc bổ sung được xác định từ tam giác vận tốc:

$$\begin{align} v_{\text{bổ sung}} &=2v_1\sin\frac{\varphi}{2} =60\,\text{km/s}\cdot\sin41^\circ\\ &=60\,\text{km/s}\cdot0.656 =39.4\,\text{km/s}. \end{align}$$

Tổng vectơ của vận tốc bổ sung với vận tốc quỹ đạo của Trái Đất cho vận tốc nhật tâm ở “đầu ra” sau khi vượt qua trường hấp dẫn của Trái Đất. Vì vậy năng lượng toàn phần lúc phóng phải tính cả thế năng hấp dẫn của Trái Đất:

$$\begin{align} \frac{mv_{\text{phóng}}^{2}}{2}-\frac{GM_\oplus m}{R_\oplus} &= \frac{mv_{\text{bổ sung}}^{2}}{2},\\ \frac{2GM_\oplus}{R_\oplus} &= v_{\text{thoát}}^{2},\\ v_{\text{phóng}}^{2} &= v_{\text{thoát}}^{2}+v_{\text{bổ sung}}^{2},\\ v_{\text{phóng}} &= \sqrt{11.2^{2}+39.4^{2}}\;\text{km/s}=41\;\text{km/s}. \end{align}$$

Bài toán 7. Quỹ đạo hypebol bay sượt hành tinh: khoảng cách tiếp cận tối thiểu và góc lệch quỹ đạo

Khi đi vào “vùng ảnh hưởng” của một hành tinh khối lượng $M$, một vật thể vũ trụ có vận tốc tương đối so với hành tinh là $v_0$ và tham số ngắm (khoảng cách va chạm) $b$. Vật thể sẽ đi qua hành tinh ở khoảng cách tối thiểu nào và vận tốc của nó bị đổi hướng một góc bao nhiêu do trường hấp dẫn của hành tinh?

Với điều kiện đã cho, quỹ đạo của vật đối với hành tinh là một hypebol, trong đó tâm hút nằm ở một tiêu điểm. Hướng vận tốc lúc đi vào và lúc đi ra trùng với các tiệm cận của hypebol; góc đổi hướng của vận tốc là góc giữa hai tiệm cận, ký hiệu $\varphi$. Tại đỉnh $A$, vận tốc vuông góc với hướng đến tiêu điểm $F$. Xét hai trạng thái: (1) lúc vật đi vào vùng ảnh hưởng, và (2) lúc vật ở đỉnh $A$; ta viết bảo toàn năng lượng và mômen động lượng:

$$\begin{align} \frac{mv_0^{2}}{2} &= \frac{mv_1^{2}}{2}-\frac{GMm}{r_1},\\ mv_0b &= mv_1r_1. \end{align}$$

Suy ra

$$\begin{align} v_1 &= \frac{b}{r_1}\,v_0,\\ \frac{2GM}{r_1} &= \frac{b^{2}-r_1^{2}}{r_1^{2}}\,v_0^{2}, \qquad \text{hay}\qquad \frac{2GM}{v_0^{2}}=\frac{b^{2}-r_1^{2}}{r_1}\;(*). \end{align}$$

$$r_1=-\frac{GM}{v_0^{2}}+\sqrt{\left(\frac{GM}{v_0^{2}}\right)^{2}+b^{2}}.$$

Ta thu được biểu thức xác định khoảng cách tiếp cận tối thiểu $r_1$ theo $v_0$ và $b$. Để tìm góc đổi hướng $\varphi$, xét hình học hypebol (xem Hình 1). Khoảng cách giữa hai tiêu điểm:

$$FF' = 2(r_1+a)=\frac{2b}{\cos(\varphi/2)}.$$

Theo tính chất cơ bản của hypebol, hiệu khoảng cách từ một điểm bất kỳ đến hai tiêu điểm là không đổi. Áp dụng cho đỉnh hypebol $A$ và cho một điểm rất xa trên quỹ đạo (khi các hướng đến hai tiêu điểm gần như song song), ta có:

$$\Delta r = 2a_1=\frac{2b}{\cos(\varphi/2)}-2r_1,\qquad \Delta r = 2a = 2b\,\tan\frac{\varphi}{2}.$$

Từ tam giác vuông $DFO$:

$$\tan\frac{\varphi}{2}=\frac{a}{b},\qquad \cos\frac{\varphi}{2}=\frac{b}{r_1+a},$$

suy ra

$$\frac{b^{2}-r_1^{2}}{2r_1}=a,\qquad \tan\frac{\varphi}{2}=\frac{b^{2}-r_1^{2}}{2br_1}.$$

Kết hợp với biểu thức $(*)$ ta được:

$$\varphi = 2\arctan\!\left(\frac{GM}{bv_0^{2}}\right).$$

Vật rời khỏi vùng ảnh hưởng của hành tinh với độ lớn vận tốc tương đối bằng đúng khi đi vào. Nhưng vận tốc nhật tâm vận tốc, tức là tổng vectơ của vận tốc tương đối của vật đối với hành tinh và vận tốc của chính hành tinh, có thể thay đổi đáng kể, kéo theo quỹ đạo cũng thay đổi. Nếu bảo đảm cho tàu vũ trụ bay sượt gần hành tinh, ta có thể thay đổi vận tốc nhật tâm và quỹ đạo của nó nhờ trường hấp dẫn của hành tinh.

Bài toán 8. Vượt vận tốc vũ trụ cấp ba: vận tốc thoát theo hệ nhật tâm và góc tiệm cận quỹ đạo hypebol

Một tàu vũ trụ xuất phát từ Trái Đất với vận tốc $v_0$ lớn hơn vận tốc vũ trụ cấp ba, theo hướng chuyển động quỹ đạo của Trái Đất (tức vuông góc với hướng về phía Mặt Trời). Khi ra khỏi “vùng ảnh hưởng” của Trái Đất, quỹ đạo của tàu trong hệ nhật tâm là một hypebol (Hình 2), có đỉnh $E$ (Trái Đất) và tiêu điểm $S$ (Mặt Trời). Hãy xác định độ lớn vận tốc $v_k$ của tàu so với Mặt Trời ở rất xa Mặt Trời. Vận tốc đó hợp với hướng $ES$ một góc $\alpha$ bằng bao nhiêu?

Hình 2

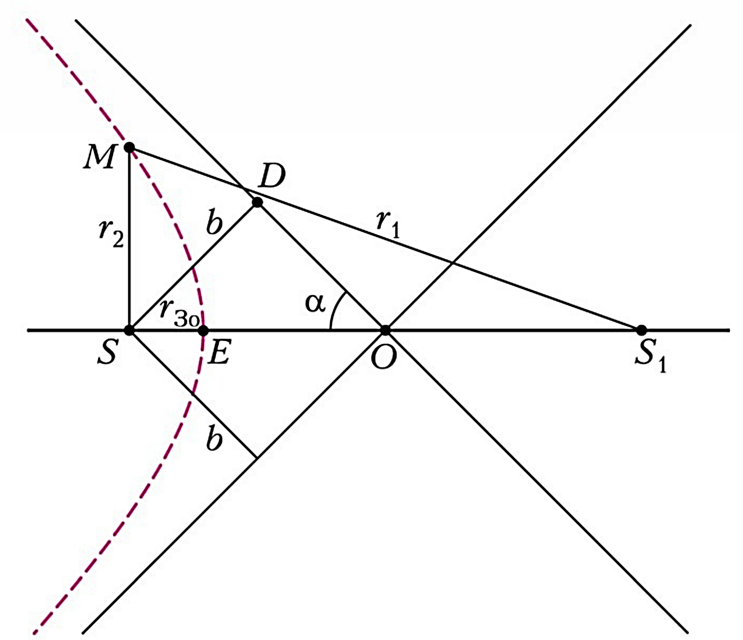
Khi rời khỏi vùng ảnh hưởng của Trái Đất, tàu có vận tốc tương đối so với Trái Đất là $v$. Theo định luật bảo toàn năng lượng (trong trường hấp dẫn của Trái Đất),

$$\frac{mv_0^2}{2}-\frac{GM_\oplus m}{R_\oplus}=\frac{mv^2}{2}.$$

Mà $\dfrac{2GM_\oplus}{R_\oplus}=v_{\text{thoát}}^2$, trong đó $v_{\text{thoát}}=11.2\,\text{km/s}$ là vận tốc thoát (vận tốc “parabol”) của Trái Đất. Do đó

$$v=\sqrt{v_0^2-v_{\text{thoát}}^2}.$$

Theo giả thiết, vận tốc bổ sung $v$ cùng hướng với vận tốc quỹ đạo của Trái Đất, nên vận tốc nhật tâm của tàu tại “đỉnh hypebol” là

$$v_r=v+v_{\text{orb}},$$

trong đó $v_{\text{orb}}=29.8\,\text{km/s}$ là vận tốc quỹ đạo của Trái Đất quanh Mặt Trời. Khi bay ra xa trong trường hấp dẫn của Mặt Trời, vận tốc nhật tâm giảm xuống còn $v_k$. Theo bảo toàn năng lượng trong trường hấp dẫn của Mặt Trời,

$$\frac{mv_r^2}{2}-\frac{GM_\odot m}{r_{\oplus 0}}=\frac{mv_k^2}{2}.$$

Với $\dfrac{GM_\odot}{r_{\oplus 0}}=v_{\text{orb}}^2$, ta được

$$v_r^2-2v_{\text{orb}}^2=v_k^2,$$

hay cuối cùng

$$v_k=\sqrt{\left(\sqrt{v_0^2-v_{\text{thoát}}^2}+v_{\text{orb}}\right)^2-2v_{\text{orb}}^2}.$$

Tàu chuyển động trong trường hấp dẫn của Mặt Trời theo một nhánh hypebol; khi đó mômen động lượng được bảo toàn. Gọi $b$ là tham số ngắm (impact parameter) của tàu đã “thoát”, ta có

$$mv_r\,r_{\oplus 0}=mv_k\,b,\qquad b=\frac{v_r}{v_k}\,r_{\oplus 0}.$$

Từ Hình 2: $ES=r_{\oplus 0}$ là bán kính quỹ đạo Trái Đất, $OE=a$ là khoảng cách từ tâm hypebol đến đỉnh. Góc cần tìm $\alpha$ là góc mà tiệm cận hypebol tạo với hướng $ES$. Theo tính chất cơ bản của hypebol, hiệu khoảng cách từ mọi điểm đến hai tiêu điểm $S$ và $S_1$ là không đổi. Áp dụng cho đỉnh $E$ và cho một điểm rất xa $M$ (khi các hướng đến hai tiêu điểm gần như song song), ta thu được:

$$r_1-r_2=2a,\qquad r_1-r_2=\frac{2b}{\tan\alpha},$$

suy ra

$$\tan\alpha=\frac{b}{a}.$$

Biểu diễn $a$ từ tam giác vuông có hai cạnh góc vuông $a$ và $b$, cạnh huyền $a+r$ (với $r=r_{\oplus 0}$):

$$\begin{align} a^2+b^2 &= a^2+2ar+r^2,\\ a &= \frac{b^2-r^2}{2r}. \end{align}$$

Thế vào (với $b=\dfrac{v_r}{v_k}r$) ta được

$$\tan\alpha=\frac{2\,\dfrac{v_r}{v_k}}{\left(\dfrac{v_r}{v_k}\right)^2-1}, \qquad \alpha=\arctan\!\left(\frac{2\,\dfrac{v_r}{v_k}}{\left(\dfrac{v_r}{v_k}\right)^2-1}\right).$$

Bài toán 9. Vượt vận tốc vũ trụ cấp ba: vận tốc thoát theo hệ nhật tâm và góc tiệm cận quỹ đạo hypebol

Một tàu vũ trụ, khi thực hiện “cú hích hấp dẫn” (gravity assist) trong vùng lân cận Sao Hỏa, đi vào một quỹ đạo nhật tâm mới; trên quỹ đạo này nó gặp một tiểu hành tinh tại điểm viễn nhật. Điểm chuyển sang quỹ đạo mới ứng với tham số tiêu (tham số quỹ đạo) của elip; tại đó tàu chuyển động theo hướng bán trục nhỏ của quỹ đạo. Chu kỳ chuyển động trên quỹ đạo mới là 10 năm. Ở điểm chuyển quỹ đạo, các tấm pin Mặt Trời được bung ra với diện tích $30\,\text{m}^2$ và hiệu suất $25\%$. Hãy ước lượng năng lượng Mặt Trời mà tàu thu được trong thời gian bay. Độ lệch tâm của quỹ đạo mới bằng bao nhiêu?

Dùng phương trình elip trong tọa độ cực:

$$r(\varphi)=\frac{p}{1+e\cos\varphi},$$

trong đó $p$ là tham số tiêu (tham số quỹ đạo), $e$ là độ lệch tâm, $\varphi$ là góc giữa vectơ bán kính $r$ và hướng từ tiêu điểm đến cận nhật (dị thường thật). Từ phương trình suy ra: tại điểm chuyển quỹ đạo $r_0=p$ khi $\cos\varphi_0=0$, tức $\varphi_0=\dfrac{\pi}{2}$; còn tại viễn nhật thì $\varphi_k=\pi$.

Chu kỳ xác định bán trục lớn $a$ theo định luật Kepler thứ ba. Nếu $a$ tính bằng AU và $T$ tính bằng năm, thì

$$\begin{align} a &= T^{2/3} = 4.64\,\text{AU}. \end{align}$$

Tham số $p$ liên hệ với $a$ bởi $p=a(1-e^2)$, và trong bài toán này $p$ đúng bằng khoảng cách nhật tâm của Sao Hỏa, tức $p=1.52\,\text{AU}$. Do đó

$$\begin{align} p &= a(1-e^2)=1.52\,\text{AU},\\ e &= \sqrt{1-\frac{p}{a}}=0.82. \end{align}$$

Bán trục nhỏ:

$$b=a\sqrt{1-e^2}=2.66\,\text{AU}.$$

Tấm pin hướng về phía Mặt Trời. Với độ trưng (công suất bức xạ) của Mặt Trời $L=3.86\cdot10^{26}\,\text{W}$, trong một khoảng thời gian rất nhỏ $dt$ tại khoảng cách $r$, năng lượng thu được là

$$dW=\eta S\,\frac{L}{4\pi r^2}\,dt,\qquad (1)$$

trong đó $\eta$ là hiệu suất, $S$ là diện tích tấm pin. Tốc độ quét diện tích của vectơ bán kính là hằng số (định luật Kepler 2):

$$\begin{align} \dot{\vec s} &= [\vec r\times\vec v],\\ |\dot{\vec s}| &= r\,v_n = r^2\omega, \end{align}$$

với $\omega=\dfrac{d\varphi}{dt}$ là tốc độ góc của vectơ bán kính. Biểu diễn tốc độ quét diện tích qua chu kỳ, ta được

$$\begin{align} \omega &= \frac{2\pi ab}{T}\cdot\frac{1}{r^2} = \frac{d\varphi}{dt}, \end{align}$$

suy ra

$$dt=\frac{Tr^2}{2\pi ab}\,d\varphi. \qquad (2)$$

Thế (2) vào (1) ta nhận được quan hệ giữa các vi phân:

$$dW=\eta S\,\frac{L}{4\pi r^2}\cdot\frac{Tr^2}{2\pi ab}\,d\varphi.$$

Chuyển sang năng lượng toàn phần trên đoạn bay. Vì $\varphi_{\text{tổng}}=\pi-\dfrac{\pi}{2}=\dfrac{\pi}{2}$, nên năng lượng thu được trên đoạn quỹ đạo này là

$$W_{\text{tổng}}=\eta S\,\frac{LT}{16\pi ab}.$$

Lấy $1\,\text{AU}=1.5\cdot10^{11}\,\text{m}$ và $T=31.56\cdot10^{7}\,\text{s}$. Khi đổi $a$ sang mét và $T$ sang giây, ta ước lượng được:

$$W_{\text{tổng}}\approx 2\cdot10^{9}\,\text{J}.$$

III. Các bài tập tự giải về chuyển động của các thiên thể trong trường hấp dẫn

1. Từ chu kỳ quay của Trái Đất và bán kính quỹ đạo Trái Đất, hãy ước lượng khối lượng Mặt Trời. Mật độ trung bình của vật chất Mặt Trời bằng bao nhiêu nếu đường kính góc của đĩa Mặt Trời quan sát từ Trái Đất là $32$ phút cung?
2. Hai ngôi sao có khối lượng xấp xỉ như nhau $m$ quay quanh tâm khối chung. Khoảng cách giữa hai sao là $R$. Chu kỳ quay của hệ bằng bao nhiêu?
3. Một tàu vũ trụ xuất phát từ bề mặt Trái Đất. Vận tốc tối thiểu ngay sau khi phóng cần có để đạt tới quỹ đạo Sao Hỏa (bán kính $r=1.52\,\text{AU}$) là bao nhiêu, nếu bỏ qua ảnh hưởng của khí quyển?
4. Sao chổi Halley có cận nhật cách Mặt Trời $0.6\,\text{AU}$. Chu kỳ của nó là $76$ năm. Ở viễn nhật, sao chổi sẽ cách Mặt Trời bao nhiêu?

---

Lời kết

Nếu coi mỗi bài toán trong bài là một “mảnh ghép”, thì hai nguyên lý bảo toàn (mômen động lượng và năng lượng) chính là “chìa khoá chung” để mở hầu hết các bài toán quỹ đạo trong trường hấp dẫn. Bạn có thể dùng bài này như một trang tổng hợp công thức khi ra đề, chữa đề hoặc luyện đội tuyển HSG/Olympic.

Bạn muốn mình soạn thêm một bộ 20–30 bài tập chọn lọc kèm phân loại mức độ (HSG tỉnh → HSG QG → Olympic) không? Nếu có, bạn cho mình biết mức bạn muốn và dạng đề bạn hay gặp, mình sẽ gợi ý cấu trúc bộ bài cho đúng nhu cầu.