Vì sao thường xuyên hít thở sâu thì cơ thể sẽ khỏe mạnh?

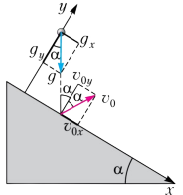
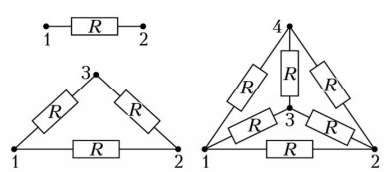
Vì sao hít thở sâu giúp cơ thể khỏe mạnh hơn trong môi trường hiện nay? Giữa nhịp sống đô thị, phòng máy lạnh kín cửa, khói bụi và thói quen ngồi nhiều, điều làm chúng ta “mệt mỏi âm thầm” không chỉ là thiếu vận động — mà còn là chất lượng không khí và cách chúng ta thở mỗi ngày. Bài viết này giải thích một cách dễ hiểu nhưng có cơ sở khoa học: vì sao cơ thể cần cả O₂ lẫn CO₂, vì sao cảm giác “ngột ngạt” trong phòng kín thường đến từ CO₂ tích tụ chứ không phải thiếu oxy, và vì sao thở sâu – thở đúng có thể giúp bạn tỉnh táo hơn, ngủ tốt hơn và cải thiện sức bền. Đồng thời, bạn sẽ có những gợi ý thực tế để cải tạo bầu không khí sống: cách thông gió hiệu quả, hiểu về ngưỡng CO₂ trong không gian kín, và những thói quen nhỏ giúp “làm mới” môi trường của bạn mỗi ngày.

Trong bài viết này, chúng ta sẽ nói về tác động của oxy và khí cacbonic \(\big(\mathrm{CO_2}\big)\) lên con người — xét riêng rẽ và xét cùng nhau.

Một góc nhìn đang thu hút sự quan tâm hiện nay là xem vấn đề như một “cái nhìn kép”: vừa từ phía không khí được hít vào, vừa từ phía bên trong — tức là trong chính cơ thể. Nói theo cách khoa học hơn: vừa từ phía hô hấp ngoài (trao đổi giữa khí quyển và các tế bào trong phổi), vừa từ phía hô hấp trong (các quá trình trong tế bào và mô của cơ thể).

Giá trị trung bình của áp suất khí quyển ở mực nước biển xấp xỉ \(p_{\text{atm}} = 760\,\text{mmHg}\). Áp suất riêng phần của oxy vào khoảng \(160\,\text{mmHg}\), tương ứng gần \(21\%\). Oxy được cơ thể hấp thụ một phần, còn \(\mathrm{CO_2}\) được tạo ra như sản phẩm của các phản ứng oxy hóa.

Thành phần của không khí hít vào và thở ra được nêu trong bảng dưới đây.

	\(\mathrm{O_2}\)	\(\mathrm{CO_2}\)	\(\mathrm{Ar}\)	\(\mathrm{N_2}\)
Không khí hít vào	21%	0,04%	0,9%	78%
Không khí thở ra	16%	4%	0,9%	78%

Bảng 1. Thành phần không khí hít vào và thở ra

Những con số này nói lên điều gì? Nitơ và argon hầu như không được cơ thể con người sử dụng (chúng là các khí trơ). Mức độ “hấp thụ” oxy không lớn — khoảng \(0{,}25\). Sau khi hít vào, cơ thể lại thở ra phần lớn lượng oxy. \(\mathrm{CO_2}\) gần như không có trong không khí hít vào nhưng lại được tạo ra tích cực trong các phản ứng oxy hóa của cơ thể.

Tỉ lệ oxy bị cơ thể “lấy đi” (21% → 16% tức giảm 5%) khá gần với tỉ lệ \(\mathrm{CO_2}\) được tạo ra (4%).

Tính trơ của nitơ và argon trong các quá trình trao đổi chất đã từng dẫn tới ý tưởng “loại bỏ” chúng khi phải sống lâu trong không gian kín. Theo hướng đó, các phi hành gia Mỹ trong những chuyến bay vũ trụ đầu tiên đã chuyển sang thở oxy tinh khiết. Khi chỉ dùng \(\mathrm{O_2}\), áp suất làm việc thấp hơn áp suất khí quyển và vào khoảng \(260\text{–}280\,\text{mmHg}\).

Tuy nhiên, khi thời gian bay tăng lên, trong môi trường oxy tinh khiết, các phi hành gia bắt đầu gặp vấn đề với đường hô hấp. Hơn nữa, khí quyển oxy tinh khiết cũng nguy hiểm hơn. Các nhà du hành vũ trụ Liên Xô/Nga ngay từ đầu đã sử dụng hỗn hợp không khí gần giống trên Trái Đất, dù điều đó đòi hỏi hệ thống tái sinh không khí phức tạp hơn. Ngày nay, trong các chuyến bay vũ trụ và trong tàu ngầm, người ta dùng thành phần khí quyển kiểu Trái Đất.

Góc nhìn từ bên ngoài

Khoảng nồng độ oxy trong không khí phù hợp cho sự sống

Khoảng giá trị của áp suất riêng phần oxy \(p_{\mathrm{O_2}}\) trong không khí, trong đó con người có thể duy trì hoạt động sống trong thời gian dài, bị giới hạn bởi:

$$90\text{–}100\,\text{mmHg} < p_{\mathrm{O_2}} < 400\text{–}450\,\text{mmHg}.$$

Giới hạn dưới tương ứng với sự khởi phát của thiếu oxy, còn giới hạn trên là sự khởi phát của ngộ độc oxy. Theo tỉ lệ phần trăm, thiếu oxy ở người khỏe mạnh có thể xuất hiện khi hàm lượng \(\mathrm{O_2}\) trong không khí (xấp xỉ theo tỉ số \(\,p_{\mathrm{O_2}}/p_{\text{atm}}\,\)) nhỏ hơn \(14\%\) (với \(p_{\text{atm}} = 760\,\text{mmHg}\)).

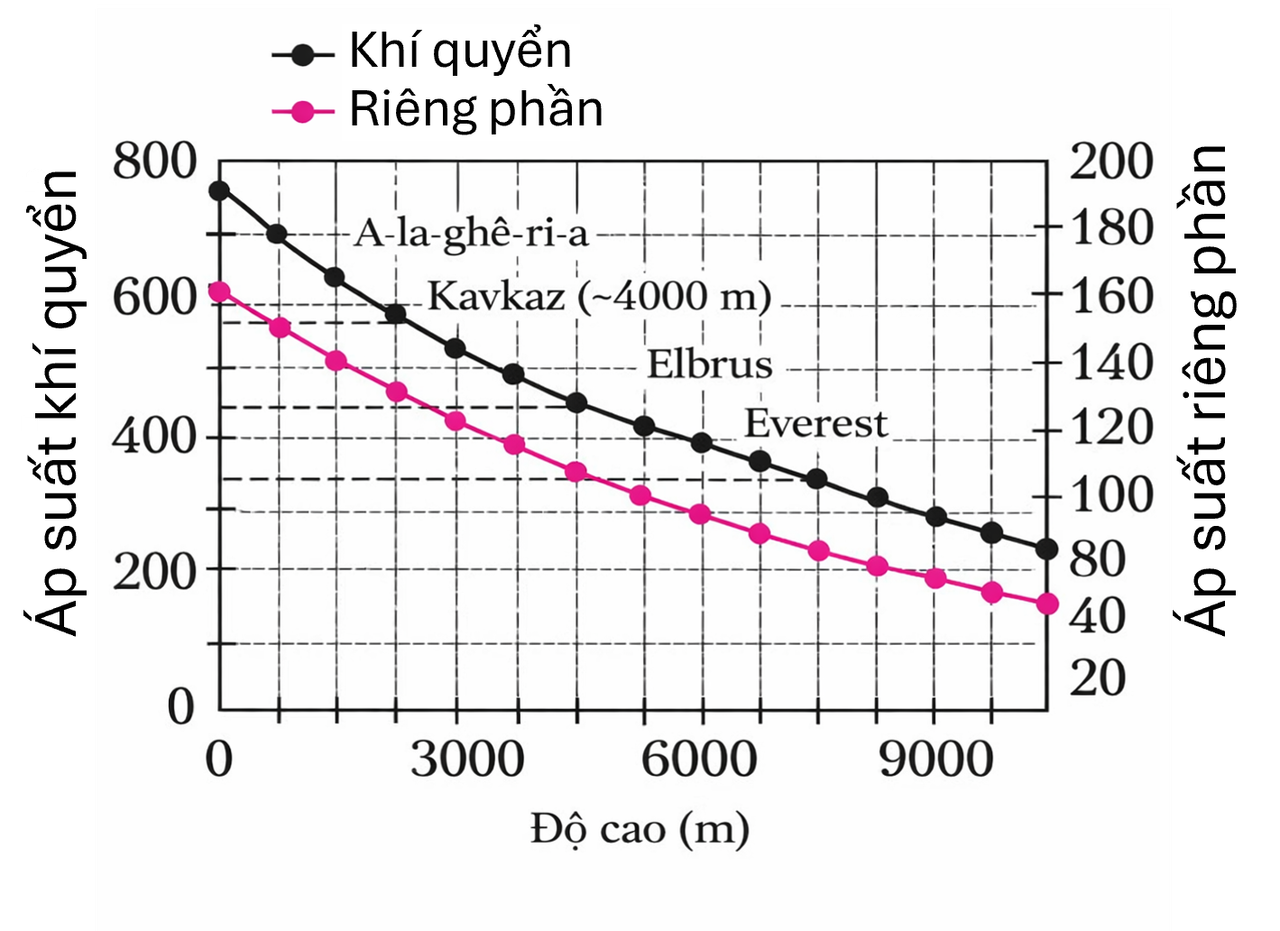
Các số liệu này tương ứng với khả năng sinh tồn ở mực nước biển. Khi lên cao, áp suất giảm, điều này được thể hiện rõ qua các đường cong của áp suất khí quyển và áp suất riêng phần oxy (xem Hình 1).

Có thể thấy rằng начиная từ độ cao khoảng \(4{,}5\text{–}5\,\text{km}\), áp suất oxy trở nên thấp hơn giới hạn dưới cho phép là \(90\,\text{mmHg}\). Khi đó, áp suất không khí trong các phế nang vào khoảng \(105\text{–}110\,\text{mmHg}\), cũng khá gần giới hạn dưới. (Phần tiếp theo ở trang sau…)

Hình 1. Sự phụ thuộc của áp suất khí quyển và áp suất riêng phần của oxy (mmHg) theo độ cao so với mực nước biển (m). Trên hình có đánh dấu độ cao của các trại leo núi, dãy Kavkaz, Elbrus và Everest.

Khi áp suất riêng phần oxy giảm xuống mức khoảng \(100\,\text{mmHg}\), các quá trình trao đổi trong cơ thể chậm lại; nhịp thở và nhịp tim tăng; thị lực và hoạt động của não suy giảm… Vì vậy ở độ cao lớn, con người không thể sống thường xuyên, lâu dài. Ngược lại, gần giới hạn trên của áp suất oxy, \(\mathrm{O_2}\) bắt đầu gây kích ứng đường hô hấp trên: xuất hiện khô rát cổ họng, ho…

Ước tính thời gian phát triển thiếu oxy khi ở trong không gian kín

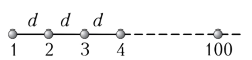
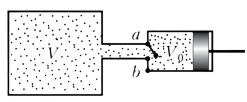
Để minh họa, ta xét một vài tình huống có người ở trong không gian kín: một người bị kẹt trong thang máy có thể tích \(V=2\,\text{m}^3\); hai người trong phòng có \(V=30\,\text{m}^3\); một trăm người bị kẹt trong toa metro đã dừng, với \(V=250\,\text{m}^3\).

Trong mỗi trường hợp, ta ước tính thời gian \(\Delta t\) để nồng độ \(\mathrm{O_2}\) trong thể tích kín \(V\) (khi mọi người thở yên tĩnh) giảm từ mức ban đầu \(21\%\) xuống ngưỡng bắt đầu thiếu oxy, tức \(14\%\). Nhấn mạnh: là thở yên tĩnh, vì khi hoảng loạn thời gian này sẽ giảm mạnh.

Với thở yên tĩnh, mức tiêu thụ oxy xấp xỉ \(0{,}25\,\text{L/min}\). Vì \(1\) lít \(\mathrm{O_2}\) tương ứng khoảng \(5\,\text{kcal}\) năng lượng, nên \(0{,}25\,\text{L/min}\) tương đương:

$$0{,}25\times 5\times 60\times 24 \approx 1800\,\text{kcal/day}.$$

Do mật độ cơ thể người khoảng \(\rho \approx 1000\,\text{kg/m}^3\), một người \(70\,\text{kg}\) chiếm thể tích khoảng \(V_{\text{cơ thể}} \approx 0{,}07\,\text{m}^3\) (tức \(70\) lít). Tính thêm quần áo, ta lấy ước lượng thể tích “chiếm chỗ” của một người là khoảng \(0{,}1\,\text{m}^3\) (100 lít).

Thang máy

Thể tích “không khí hữu dụng” (không bị cơ thể chiếm chỗ) khoảng \(1{,}9\,\text{m}^3\). Lượng oxy ban đầu trong đó là:

$$1{,}9\times 0{,}21 = 0{,}4\,\text{m}^3 \approx 400\,\text{L}\;\mathrm{O_2}.$$

Thiếu oxy bắt đầu khi lượng oxy “hữu dụng” giảm còn:

$$1{,}9\times 0{,}14 = 0{,}27\,\text{m}^3 \approx 270\,\text{L}.$$

Như vậy lượng oxy giảm từ \(400\) xuống \(270\) lít, tức giảm \(130\) lít. Với mức tiêu thụ \(0{,}25\,\text{L/min}\), thời gian là:

$$\Delta t_{\mathrm{O_2}}=\frac{130}{0{,}25}\,\text{min}\approx 520\,\text{min}\;(\text{hơn }8\text{ giờ}).$$

Phòng

Thể tích không khí hữu dụng khoảng \(30\,\text{m}^3\). Lượng oxy ban đầu \(6{,}3\,\text{m}^3\), mức tối thiểu cho phép \(4{,}2\,\text{m}^3\). Tiêu thụ oxy \(0{,}5\,\text{L/min}\). Khi đó:

$$\Delta t_{\mathrm{O_2}}=\frac{2100}{0{,}5}\,\text{min}=4200\,\text{min}\approx 3\text{ ngày (!)}.$$

Toa tàu metro

Thể tích không khí hữu dụng khoảng \(240\,\text{m}^3\). Lượng oxy ban đầu \(50\,\text{m}^3\), mức tối thiểu cho phép \(34\,\text{m}^3\). Tiêu thụ oxy khoảng \(25\,\text{L/min}\). Khi đó:

$$\Delta t_{\mathrm{O_2}}=\frac{16000}{25}\,\text{min}\approx 640\,\text{min}\approx 10\text{ giờ}.$$

Nhận xét

Trong các trường hợp trên (nếu không hoảng loạn), thời gian để thiếu oxy xuất hiện là khá dài. Nhưng trải nghiệm đời thường lại cho thấy ở metro hoặc thang máy bị kẹt thường “ngột ngạt”; thậm chí ngủ trong phòng đóng kín cửa sổ, sáng dậy cũng có cảm giác khó thở. Nhiều khả năng còn có cơ chế mạnh hơn gây khó chịu khi ở không gian kín — không phải do thiếu \(\mathrm{O_2}\), mà do sự tích tụ \(\mathrm{CO_2}\).

Nồng độ \(\mathrm{CO_2}\) trong không khí phù hợp cho sự sống

Khoảng nồng độ \(\mathrm{CO_2}\) cho phép trong không khí được viết dưới dạng:

$$0 < C_{\mathrm{CO_2}}=\frac{p_{\mathrm{CO_2}}}{p_{\text{atm}}} < 0{,}1\%.$$

Lưu ý rằng hàm lượng \(\mathrm{CO_2}\) bình thường trong không khí là \(C_{\mathrm{CO_2}}=0{,}04\%\). Giới hạn trên chấp nhận được thường lấy \(C_{\mathrm{CO_2,\max}}=0{,}1\%\). Ta sẽ bàn kỹ hơn về giới hạn này ở phần sau; trước mắt, hãy dùng nó để đánh giá cho các không gian kín như thang máy, phòng, toa metro và cả lớp học.

Bây giờ ta áp dụng cách tính tương tự cho thời gian tích tụ nồng độ khí cacbonic đến ngưỡng trên. Giả sử một người trưởng thành trung bình thải \(\mathrm{CO_2}\) ra môi trường với lưu lượng \(q_{\mathrm{CO_2}} = 0{,}25\,\text{L/min}\).

Thang máy

Thể tích không khí hữu dụng (phần không khí tự do) trong thang máy là khoảng \(1{,}9\,\text{m}^3\). Thời gian để nồng độ \(\mathrm{CO_2}\) trong không khí tăng từ \(0{,}04\%\) lên \(0{,}1\%\) là:

$$\Delta t_{\mathrm{CO_2}} = \frac{\big(C_{\mathrm{CO_2,max}}-C_{\mathrm{CO_2}}\big)\,V}{q_{\mathrm{CO_2}}}$$

$$= \frac{(1\cdot10^{-3}-4\cdot10^{-4})\cdot 1{,}9\cdot10^{3}}{0{,}25}\,\text{min} \approx 5\,\text{min}.$$

Phòng

Thể tích không khí hữu dụng khoảng \(30\,\text{m}^3\). Thời gian để nồng độ \(\mathrm{CO_2}\) tăng từ \(0{,}04\%\) lên \(0{,}1\%\):

$$\Delta t_{\mathrm{CO_2}} = \frac{6\cdot10^{-4}\cdot 30\cdot10^{3}}{2\cdot 0{,}25}\,\text{min} = 36\,\text{min}.$$

Toa tàu metro

Thể tích không khí hữu dụng khoảng \(240\,\text{m}^3\). Thời gian để nồng độ \(\mathrm{CO_2}\) tăng từ \(0{,}04\%\) lên \(0{,}1\%\):

$$\Delta t_{\mathrm{CO_2}} = \frac{6\cdot10^{-4}\cdot 240\cdot10^{3}}{100\cdot 0{,}3}\,\text{min} \approx 6\,\text{min}.$$

Lớp học

Xét thêm trường hợp lớp học có thể tích khoảng \(200\,\text{m}^3\) với \(25\) học sinh. Nếu một học sinh thải \(\mathrm{CO_2}\) với lưu lượng \(0{,}12\,\text{L/min}\) (xấp xỉ một nửa so với người lớn), ta có:

$$\Delta t_{\mathrm{CO_2}} = \frac{6\cdot10^{-4}\cdot 200\cdot10^{3}}{25\cdot 0{,}12}\,\text{min} \approx 40\,\text{min}.$$

Các con số này đã gần với cảm nhận thực tế hơn, và giải thích vì sao cần thông gió: lỗ/ô thông gió ở trần thang máy, nhu cầu mở cửa sổ phòng định kỳ, đặc biệt là trong lớp học sau mỗi tiết, cũng như sự cần thiết của hệ thống thông gió trong метро.

Như vậy, chính sự tích tụ \(\mathrm{CO_2}\) trong không gian kín mới là yếu tố tác động mạnh, gây cảm giác khó chịu trước tiên. Vậy nó biểu hiện như thế nào?

Tài liệu cho thấy có hai dạng tác động: ngắn hạn (vài giờ) và dài hạn (lặp lại thường xuyên, tổng cộng nhiều giờ mỗi ngày). Với tác động ngắn hạn khi nồng độ \(\mathrm{CO_2}\) trong không khí thở vào vượt \(0{,}1\%\), có thể xuất hiện: mệt mỏi, đau đầu, giảm khả năng tập trung, ngủ kém…

Với tác động dài hạn khi mức \(\mathrm{CO_2}\) cao hơn \(0{,}1\%\), có thể xuất hiện vấn đề với hệ hô hấp (ho khan, viêm mũi…), suy giảm miễn dịch, và ухуд đi hoạt động của hệ tim mạch… Khi mức trên \(0{,}2\%\), khả năng tập trung giảm mạnh hơn, số lỗi tăng lên, v.v. theo xu hướng tăng dần.

Ghi chú

Có thể cần một giới hạn nghiêm ngặt hơn cho mức \(\mathrm{CO_2}\) cho phép trong không khí thở vào, cỡ \(0{,}06\%\text{–}0{,}08\%\). Điều này càng thu hẹp thời gian có thể ở trong phòng không thông gió.

Một vấn đề khác của phòng không thông gió là khả năng không khí bị phân tầng. Vì \(\mathrm{CO_2}\) nặng hơn không khí khoảng 1,5 lần, nó có thể “tụ” gần sàn và làm nồng độ там tăng. Tuy nhiên, quá trình này chậm, và chỉ cần có chuyển động không khí nhẹ cũng có thể trộn các lớp khí.

Cuối cùng, nhiều người nghĩ rằng trồng cây sẽ giúp vì cây nhả \(\mathrm{O_2}\) và hấp thụ \(\mathrm{CO_2}\). Nhưng điều này chủ yếu xảy ra ban ngày; вечером và ban đêm (khi không khí tươi đặc biệt cần), thực vật lại thải \(\mathrm{CO_2}\), làm vấn đề tích tụ càng nặng hơn.

Sự tích tụ khí CO trong phòng kín

Thoạt nhìn, khó hiểu vì sao khí cacbon monoxit \(\big(\mathrm{CO}\big)\) có thể xuất hiện trong phòng kín, nếu không có bếp củi hay lò sưởi thông gió kém ở gần. Tuy nhiên, tài liệu ghi nhận rằng bên cạnh \(\mathrm{CO_2}\), con người cũng thải ra một lượng nhỏ \(\mathrm{CO}\) — cỡ \(1{,}6\,\text{mL/h}\) (trong điều kiện bình thường). Nồng độ \(\mathrm{CO}\) tối đa cho phép đối với con người vào khoảng \(1\,\text{mg/m}^3\).

Các số liệu này đủ để tiếp tục ước tính thời gian tích tụ đến ngưỡng опасной концентрации của \(\mathrm{CO}\) trong thang máy, phòng, toa metro và lớp học. Để làm điều đó, ta chuyển từ thể tích sang khối lượng khí \(\mathrm{CO}\) tạo thành, dùng quan hệ quen thuộc: một mol khí ở điều kiện chuẩn chiếm thể tích \(22{,}4\,\text{L}\).

Với \(\mathrm{CO}\), khối lượng mol là \(28\,\text{g/mol}\), do đó \(1\,\text{mL}\,\mathrm{CO}\) có khối lượng khoảng \(1{,}25\,\text{mg}\). Vì vậy, mức \(1{,}6\,\text{mL/h}\) \(\mathrm{CO}\) thở ra bởi một người tương ứng khoảng \(2\,\text{mg/h}\) \(\mathrm{CO}\) đi vào không khí.

Trong Bảng 2 (ở phần tiếp theo) sẽ đưa các giá trị thời gian tích tụ của \(\mathrm{CO_2}\) và \(\mathrm{CO}\) tới các nồng độ nguy hiểm.

Bảng 2. So sánh thời gian suy giảm \(\mathrm{O_2}\) và tích tụ \(\mathrm{CO}\), \(\mathrm{CO_2}\)

Tình huống	Số người	Thể tích, \(\text{m}^3\)	Thời gian \(\downarrow\,\mathrm{O_2}\)	Thời gian \(\uparrow\,\mathrm{CO}\)	Thời gian \(\uparrow\,\mathrm{CO_2}\)
Thang máy	1	1,9	8 giờ	1 giờ	5 phút
Phòng	2	30	3 ngày	13 giờ	36 phút
Toa metro	100	240	10 giờ	\(\approx 1\) giờ	6 phút
Lớp học	25	200	—	8 giờ	40 phút

Kết luận từ Bảng 2

Có thể thấy, sự tích tụ \(\mathrm{CO_2}\) trong không gian kín nguy hiểm hơn rõ rệt so với tích tụ \(\mathrm{CO}\), và còn “nguy hiểm hơn một bậc” so với việc nồng độ \(\mathrm{O_2}\) giảm xuống ngưỡng gây thiếu oxy.

Công suất hệ thống thông gió

Làm thế nào ước tính lưu lượng thông gió \(q_{\text{vent}}\) cần thiết để duy trì thành phần không khí bình thường? Nếu bỏ qua các quá trình quá độ và giả thiết không khí được trộn đều, kết quả cuối cùng khá đơn giản:

$$q_{\text{vent}}=\frac{q_{\mathrm{CO_2}}}{\big(C_{\mathrm{CO_2,max}}-C_{\mathrm{CO_2}}\big)}.$$

Ví dụ, nếu \(q_{\mathrm{CO_2}}=0{,}25\,\text{L/min}\) (tức một người thải khoảng \(15\,\text{L}\,\mathrm{CO_2}\) mỗi giờ), với \(C_{\mathrm{CO_2,max}}=1\cdot 10^{-3}\) và \(C_{\mathrm{CO_2}}=4\cdot 10^{-4}\), ta được lưu lượng thông gió cần thiết khoảng \(420\,\text{L/min}\), tức khoảng \(25\,\text{m}^3/\text{h}\).

Nếu một người thải \(20\,\text{L}\,\mathrm{CO_2}\) mỗi giờ, lưu lượng thông gió cần tăng lên khoảng \(33\,\text{m}^3/\text{h}\). Và nếu lấy ngưỡng cho phép tối đa “chặt” hơn một chút, chẳng hạn \(C_{\mathrm{CO_2,max}}=0{,}8\cdot10^{-3}\), thì lưu lượng sẽ tăng lên khoảng \(38\,\text{m}^3/\text{h}\) (khi thải \(15\,\text{L}\,\mathrm{CO_2}/\text{h}\)) và khoảng \(50\,\text{m}^3/\text{h}\) (khi thải \(20\,\text{L}\,\mathrm{CO_2}/\text{h}\)).

Nhiều hay ít? Thông gió tự nhiên có thể “mạnh” đến mức nào?

Làm sao để đảm bảo lượng không khí tươi như vậy? Chẳng hạn, nếu mở cửa, thì chỉ cần một khe hở nhỏ ở cửa cũng tạo ra trao đổi khí. Giả sử chênh lệch áp suất hai bên cửa là \(\Delta p = 10\,\text{Pa}\). Khi đó, qua mỗi \(\text{cm}^2\) khe hở có thể đi qua khoảng \(1\,\text{m}^3\) không khí mỗi giờ. Điều này có nghĩa là với \(\Delta p\) như vậy, chỉ cần một khe hở cao khoảng 2 m và rộng 1 cm đã có thể cho lưu lượng cỡ \(200\,\text{m}^3/\text{h}\).

Mẹo thực tế

Mức chênh áp \(10\,\text{Pa}\) là khá nhỏ (cỡ \(10^{-4}\) áp suất khí quyển) và hoàn toàn có thể xảy ra. Hiệu quả thông gió còn mạnh hơn nếu mở cửa và cửa sổ trong vài phút để “xả” nhanh không khí tù.

Ví dụ thực tế: giải cứu trong hang (Thái Lan)

Để minh họa, hãy xét tình huống liên quan đến oxy và \(\mathrm{CO_2}\) trong vụ giải cứu trẻ em mắc kẹt trong hang ở Thái Lan. Năm 2018, cả thế giới theo dõi chiến dịch cứu hộ đội bóng gồm 12 thiếu niên và huấn luyện viên, bị kẹt trong hang Tham Luang suốt 18 ngày (từ 23/6 đến 10/7) do mưa lớn làm ngập lối vào. Họ trú ẩn trong một “túi khí” nằm hoàn toàn bị nước chặn phía trước và cách xa cửa hang khoảng 5 km. Việc giải cứu càng khó khăn do có một đoạn hẹp nguy hiểm trên đường thoát ra (trong hình dưới được đánh dấu là “điểm nguy hiểm”).

Hình 2. Sơ đồ hang Tham Luang: bên trái là nhóm học sinh và huấn luyện viên trong khoang khí; bên phải là lực lượng cứu hộ. Đoạn hẹp nguy hiểm được đánh dấu là “điểm nguy hiểm”.

Hình 3. Khe hẹp (“điểm nguy hiểm”). Để chui qua khe cần tháo bình khí; vì vậy mỗi em nhỏ được hai thợ lặn cứu hộ kèm. (Trong hình minh họa: khe rộng khoảng 40 cm; thợ lặn tháo bình và kéo em nhỏ qua khe.)

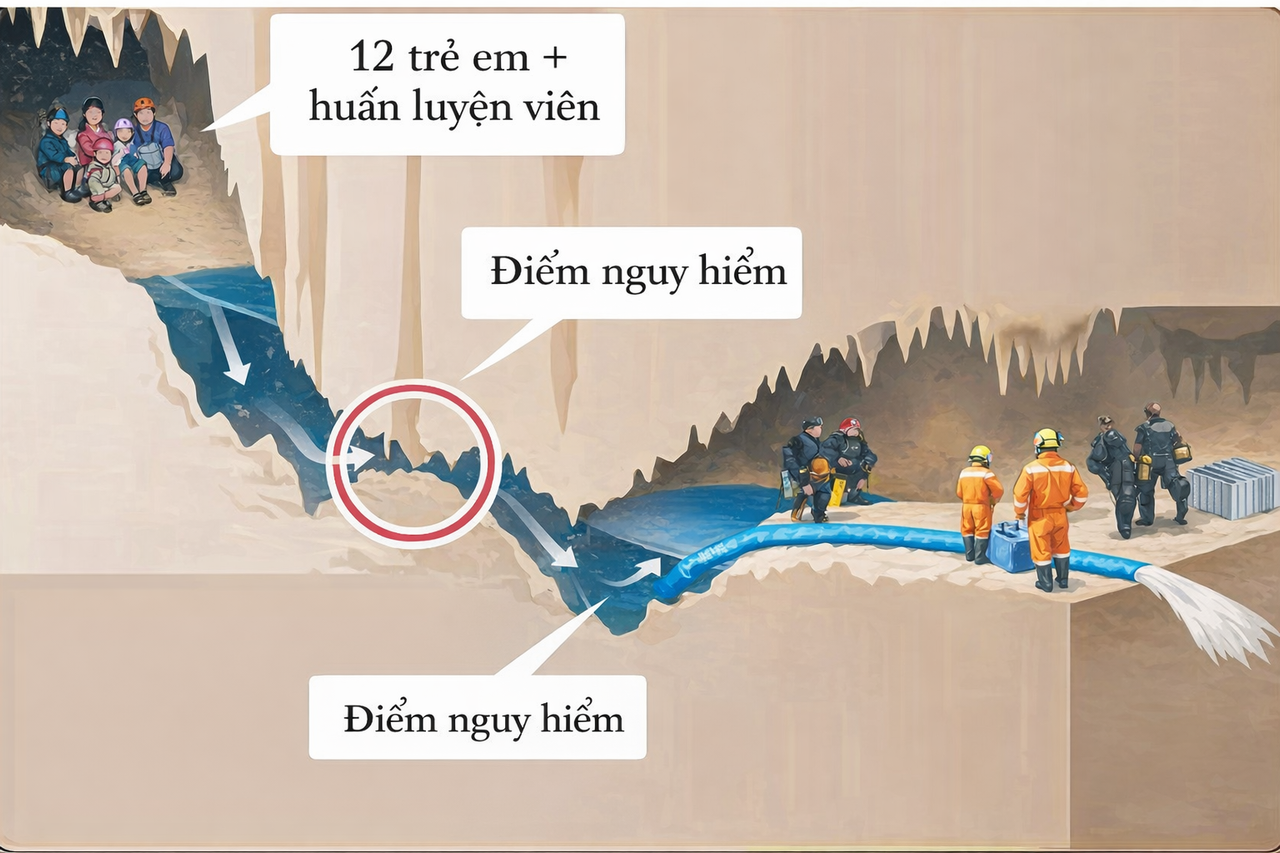
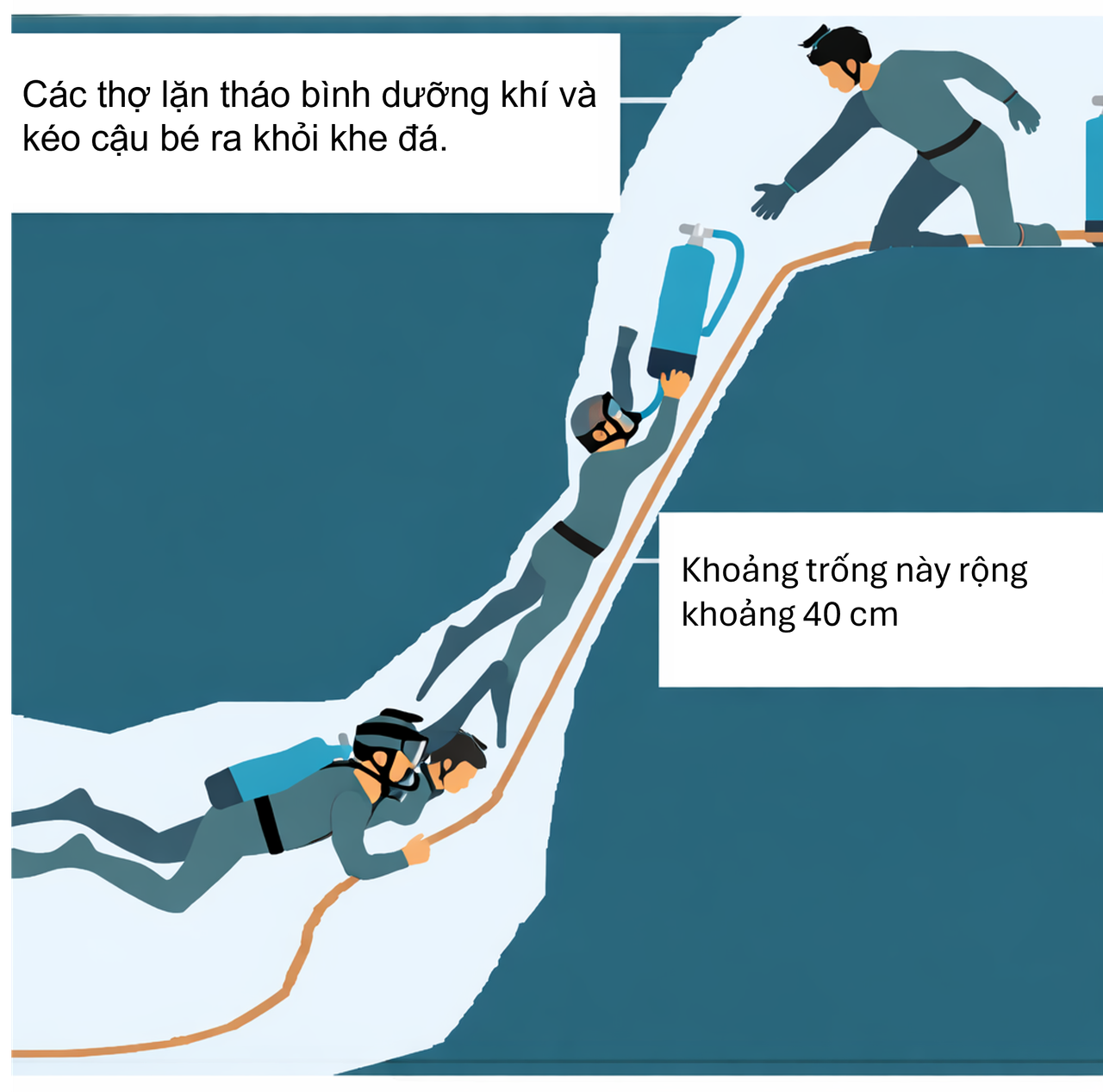
Đặc điểm của đoạn khe hẹp trên đường bơi qua được minh họa ở Hình 3. Lực lượng cứu hộ phải liên tục bơm hút nước khỏi hang. Vì vậy, trong hang có mặt rất nhiều người: người hút nước, người chuẩn bị cho trẻ em ra ngoài, bác sĩ và những người phối hợp tổ chức chiến dịch.

Trong tình huống này, tất cả những điều đã bàn về hành vi của \(\mathrm{O_2}\) và \(\mathrm{CO_2}\) trong không gian kín đều trở nên đặc biệt quan trọng. Để chống lại sự giảm dần lượng oxy trong hang, người ta tổ chức cấp oxy bằng đường ống. Đồng thời, người ta nhận ra rằng sự tích tụ \(\mathrm{CO_2}\) trong hang nguy hiểm hơn đáng kể so với việc thiếu \(\mathrm{O_2}\). Khi bơm \(\mathrm{O_2}\) vào phần trên của hang, dòng khí này đồng thời đẩy \(\mathrm{CO_2}\) ra ngoài. Cũng tính đến khả năng không khí bị phân tầng: phần \(\mathrm{CO_2}\) có xu hướng dồn xuống thấp. Đây là một trong các lý do khiến trẻ em và huấn luyện viên trú ở khu vực cao hơn trong hang.

Việc tìm kiếm và chuẩn bị cứu hộ kéo dài gần hai tuần. Trong thời gian đó, một kỹ sư/nhà sáng chế nổi tiếng là Elon Musk đã kịp chế tạo (từ các bộ phận liên quan đến tên lửa) một tàu ngầm mini cho một người và đưa tới Thái Lan. Tuy nhiên, do khe quá hẹp, phương án này không được sử dụng.

Tình hình mỗi ngày càng phức tạp. Cần sự hiện diện liên tục của những người hút nước (nếu không, hang có thể bị ngập hoàn toàn), và cần lắp đặt hệ thống ống để cấp oxy. Hơn chục thợ lặn bình khí đã vận chuyển nước, thực phẩm và các bình oxy vào sâu trong hang.

Có lúc, do \(\mathrm{CO_2}\) tích tụ, không thể chờ thêm: dọc tuyến đường từ trong hang ra cửa hang, người ta đặt nhiều bình oxy (mỗi bình tính cho khoảng một giờ sử dụng). Hàng nghìn người tham gia cứu hộ, trong đó có khoảng một trăm thợ lặn, đã bắt đầu chiến dịch. Ngày đầu, 13 thợ lặn cứu được 4 thiếu niên. Ngày thứ hai, 18 thợ lặn (cùng khoảng 70 người hộ tống) cứu thêm 4 em. Cuối cùng, ngày thứ ba, cứu nốt 4 em còn lại và huấn luyện viên, cùng 4 người vẫn ở lại trong hang. Thật đáng khâm phục!

Góc nhìn từ bên trong

Ở mức tế bào, “môi trường không khí” trong cơ thể hoàn toàn khác. Hàm lượng oxy trong tế bào thường chỉ khoảng \(1\text{–}2\%\) (ngoại lệ là hồng cầu, nơi có thể chứa tới \(96\text{–}98\%\) oxy), còn \(\mathrm{CO_2}\) trong tế bào khoảng \(6\%\). Nếu nồng độ \(\mathrm{CO_2}\) trong tế bào giảm, các vấn đề về hô hấp có xu hướng tăng lên.

Ở Hình 4 trình bày sự phụ thuộc của thời gian đặc trưng mà một người bình thường (không phải vận động viên kỷ lục) có thể nín thở, nhịp tim và mức suy giảm cấp máu… theo nồng độ \(\mathrm{CO_2}\) trong máu.

Hình 4. Mối liên hệ đặc trưng giữa thời gian nín thở (giây), nhịp tim (nhịp/phút) và mức suy giảm cấp máu (phần trăm) với nồng độ \(\mathrm{CO_2}\) trong máu.

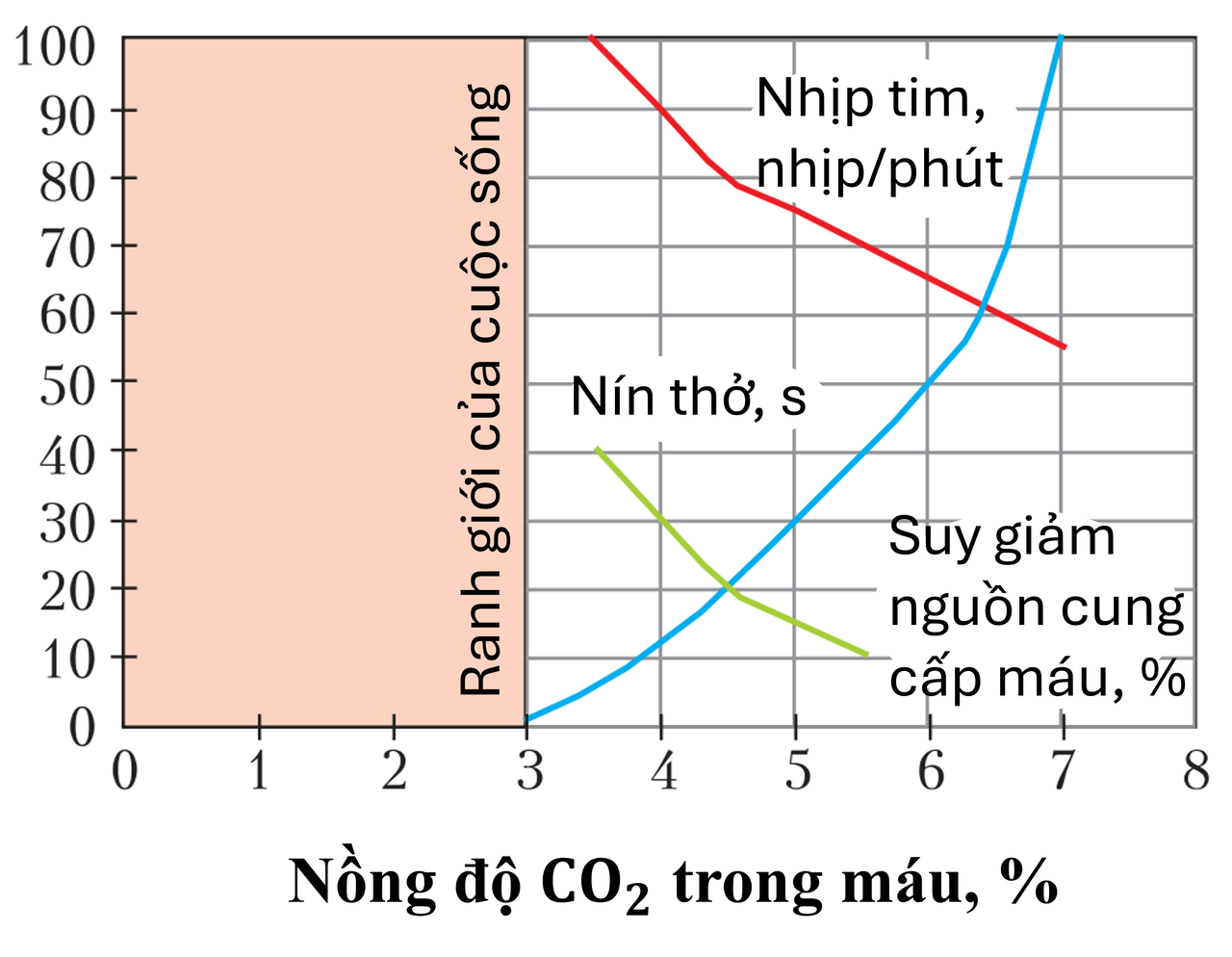
Từ các đường cong ở Hình 4 có thể rút ra kết luận chung: khi nồng độ \(\mathrm{CO_2}\) giảm, thời gian nín thở giảm; khi tiến gần mức khoảng \(3\%\), tế bào có thể bị tổn hại nghiêm trọng; nhịp tim tăng nhanh; mức tưới máu các cơ quan suy giảm. Vì vậy, nồng độ \(\mathrm{CO_2}\) “mong muốn” trong tế bào nên vào khoảng \(6\%\) hoặc thậm chí hơi cao hơn.

Bảng 3 dưới đây (trình bày hàm lượng oxy và \(\mathrm{CO_2}\) ở các “khoang” khác nhau trong cơ thể) cũng xác nhận các con số vừa nêu.

Bảng 3. Hàm lượng \(\mathrm{O_2}\) và \(\mathrm{CO_2}\)

Môi trường	\(\mathrm{O_2}\)	\(\mathrm{CO_2}\)
Không khí hít vào, \(\%\)	21	0,04
Không khí thở ra, \(\%\)	16	4
Không khí phế nang, \(\text{mmHg}\)	\(105\text{–}110\) \(\,(14\%)\)	\(40\) \(\,(5\%)\)
Máu động mạch, \(\text{mmHg}\)	\(100\)	\(40\)
Máu tĩnh mạch, \(\text{mmHg}\)	\(40\)	\(46\)
Tế bào, \(\text{mmHg}\)	\(\sim 10\)	\(60\text{–}70\)

Trong phổi diễn ra sự trao đổi \(\mathrm{O_2}\) và \(\mathrm{CO_2}\) giữa phế nang và máu. Phế nang là các cấu trúc tận cùng của phổi, giống như những “bọt khí” nhỏ, được bao quanh bởi mạng mao mạch (xem Hình 5). Qua thành phế nang (đường kính khoảng \(0{,}3\,\text{mm}\)), với số lượng phế nang trong phổi người cỡ một tỉ, và tổng diện tích bề mặt xấp xỉ \(100\,\text{m}^2\), quá trình trao đổi khí diễn ra rất mạnh: oxy đi vào máu, và gần như một lượng tương ứng \(\mathrm{CO_2}\) từ máu khuếch tán vào phổi.

Nói cụ thể hơn: trung bình trong một ngày, từ không khí phế nang vào máu đi vào khoảng \(500\,\text{L}\) oxy, đồng thời khoảng \(430\,\text{L}\) \(\mathrm{CO_2}\) từ máu đi vào không khí phế nang.

Gợi ý đọc thêm

Phần mô tả chi tiết hơn về phế nang có thể xem trong sách của K. Yu. Bogdanov: “Vật lý trong vai trò nhà sinh học” (tủ sách “Kvant”, số 49, trang 133).

Điều gì “khởi động” cơ thể: \(\mathrm{O_2}\) hay \(\mathrm{CO_2}\)?

Hãy nhớ nghịch lý quen thuộc: “cái gì có trước — con gà hay quả trứng?” Nếu không xét đến tiến hóa, câu hỏi khó có lời giải. Nhưng khi xét đến tiến hóa, “quả trứng” có vẻ “có trước” vì nó cổ xưa hơn: trứng đã xuất hiện từ thời khủng long, còn chim chỉ là một nhánh phát triển sau đó. Theo nghĩa này, “trứng” có thể xem là “nguyên thủy” hơn chim.

Tương tự, ở đây câu hỏi là: cái gì “có trước”, hay nói cách khác, cái gì kích hoạt chuỗi quá trình trong cơ thể người: \(\mathrm{O_2}\) hay \(\mathrm{CO_2}\)? Trước kia người ta thường xem \(\mathrm{O_2}\) là первичным vì nó là nguồn năng lượng chủ yếu, thúc đẩy các quá trình sinh học. Nhưng hiện nay “con lắc” quan điểm đang nghiêng về phía \(\mathrm{CO_2}\). Người ta dần đi đến kết luận rằng chính sự tích tụ \(\mathrm{CO_2}\) trong cơ thể mới là cơ chế “khởi động” ban đầu.

Khi \(\mathrm{CO_2}\) tích tụ trong cơ thể (do chuyển hóa chất béo và protein trong tế bào), nó tạo tín hiệu cho não rằng cần phải đưa \(\mathrm{CO_2}\) ra khỏi tế bào. \(\mathrm{CO_2}\) “bám” vào hồng cầu và được vận chuyển đến phế nang của phổi. Trên những “chỗ trống” vừa giải phóng trong “chuyến tàu” hồng cầu, \(\mathrm{O_2}\) sẽ “lên chỗ” và được mang đi khắp cơ thể.

Cách nhìn hiện đại về hô hấp

Trình tự đúng hơn là: trước hết thở ra \(\mathrm{CO_2}\), sau đó mới hít vào \(\mathrm{O_2}\). Đồng thời, cùng với \(\mathrm{CO_2}\) ta cũng thở ra một phần oxy dư thừa.

Hình 5. Phế nang được bao quanh bởi mao mạch. Minh họa đường đi: \(\mathrm{O_2}\) đi vào hồng cầu, còn \(\mathrm{CO_2}\) đi ra khỏi hồng cầu vào không khí phế nang.

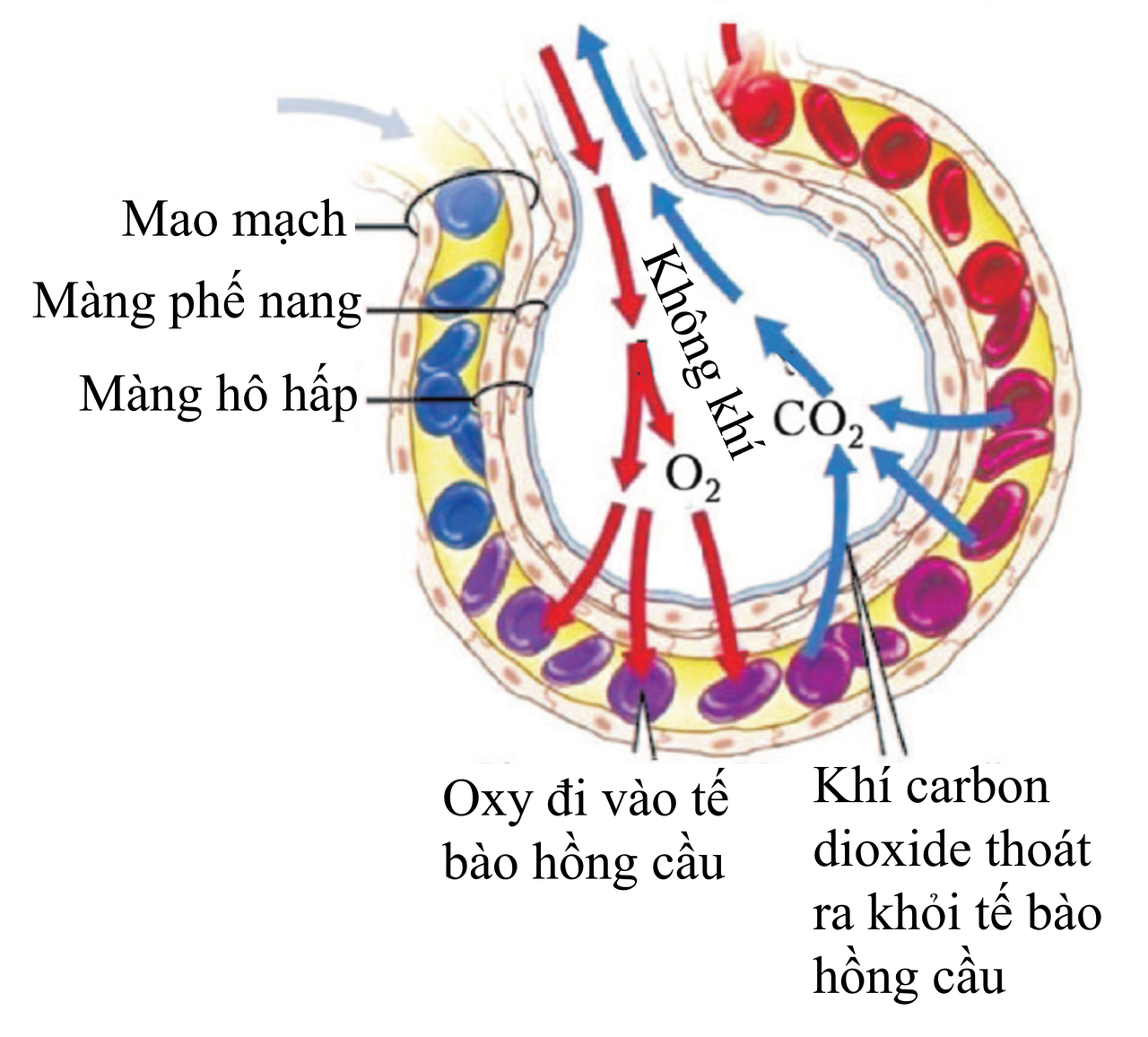
Để hô hấp, cơ thể cần cả hai khí, được hồng cầu “chở” luân phiên. Máu tĩnh mạch có màu đỏ sẫm chủ yếu do \(\mathrm{CO_2}\), còn máu động mạch có màu đỏ tươi do \(\mathrm{O_2}\).

Tỉ lệ trung bình giữa lượng \(\mathrm{CO_2}\) và \(\mathrm{O_2}\) trong cơ thể người khỏe mạnh xấp xỉ \(3{:}1\) (khoảng \(6\%\ \mathrm{CO_2}\) và \(2\%\ \mathrm{O_2}\)).

Tương tác “bên ngoài” và “bên trong”

Như vậy, \(\mathrm{CO_2}\) là khí cần thiết cho sự sống và việc duy trì một mức \(\mathrm{CO_2}\) nhất định trong cơ thể là quan trọng. Thiếu \(\mathrm{CO_2}\) hay thừa \(\mathrm{CO_2}\) đều có hại.

Tích tụ \(\mathrm{CO_2}\) quá cao thường xảy ra trong phòng kém thông gió: khi \(\mathrm{CO_2}\) trong không khí thở vào lớn (trên khoảng \(0{,}08\%\text{–}0{,}1\%\)) thì mức \(\mathrm{CO_2}\) trong cơ thể cũng tăng (hậu quả đã thảo luận ở các phần trước). Nhưng thiếu \(\mathrm{CO_2}\) trong máu (dưới khoảng \(4\%\)) cũng nguy hiểm (xem Hình 4).

Khi nào có thể bị thiếu \(\mathrm{CO_2}\)?

Trường hợp điển hình là thở quá nhanh: ta thở ra quá nhiều \(\mathrm{CO_2}\) nên trong cơ thể còn lại quá ít. Khi thiếu \(\mathrm{CO_2}\), oxy bị “giữ chặt” vào hemoglobin trong hồng cầu. Ngay cả khi trong máu có nhiều \(\mathrm{O_2}\), nó vẫn ở dạng liên kết và khó đi vào mô. Nếu trong tình trạng đó lại cố thở nhanh hơn nữa thì chỉ làm vấn đề nặng thêm.

Vậy nên làm gì?

Vận động, tập гимнастика, chơi thể thao ngoài trời hoặc trong phòng thông thoáng — tất cả đều có xu hướng giúp tăng mức \(\mathrm{CO_2}\) phù hợp. Mao mạch giãn ra, thậm chí hình thành thêm mạng mao mạch mới; lưu lượng máu tăng; oxy tách khỏi hemoglobin tốt hơn và đi vào tế bào hiệu quả hơn.

Có một ví dụ khác cho thấy lợi ích của nhịp thở chậm hơn: trong chạy bộ, vận động viên đôi khi được khuyên (khi đã mệt) hãy cố nín thở lâu hơn một chút để “mở” trạng thái gọi là “hơi thở thứ hai”, nhờ đó có thể tiếp tục chạy.

Sơ cứu: hô hấp nhân tạo “miệng kề miệng”

Trong sơ cứu khi nạn nhân ngừng thở, một phương pháp hiệu quả là hô hấp nhân tạo “miệng kề miệng” (kết hợp với ép tim ngoài lồng ngực). Người cứu (thổi) thường được hướng dẫn thổi vào nạn nhân với tần số khoảng \(12\text{–}15\) lần mỗi phút.

Nghe có vẻ vô lý, vì ở đầu bài ta đã nhấn mạnh thành phần không khí hít vào là khoảng \(21\%\ \mathrm{O_2}\) và \(0{,}04\%\ \mathrm{CO_2}\). Nhưng khi thổi “không khí thở ra”, ta đang đưa vào hỗn hợp khoảng \(16\%\ \mathrm{O_2}\) và \(4\%\ \mathrm{CO_2}\). Dù vậy, trong không khí thở ra vẫn còn oxy với nồng độ cao hơn mức tối thiểu cho phép \((16\% > 13\text{–}14\%)\). Đồng thời, nồng độ \(\mathrm{CO_2}\) cao hơn lại có ích vì nó kích thích trung khu hô hấp của não, giúp khởi phát phản xạ thở và góp phần làm “mở” phế nang.

So sánh dễ hiểu

Tình huống này có chút tương tự sơ cứu khi tim ngừng đập: người cứu cần làm rung/chấn động lồng ngực (ví dụ đánh/đập đúng kỹ thuật) để “kích hoạt” lại hoạt động tim. Với hô hấp, vai trò của \(\mathrm{CO_2}\) trong cấp cứu vì vậy cũng khác so với trong nhịp thở спокойный thường ngày.

Cách tăng nồng độ \(\mathrm{CO_2}\) trong không khí thở ra

Trong cuộc sống hằng ngày, con người ở “chế độ tự động” thường thực hiện khoảng \(15\) chu kỳ hít–thở mỗi phút (mỗi chu kỳ kéo dài xấp xỉ \(4\) giây). Tỉ lệ thời gian hít vào và thở ra thường vào khoảng \(1:1{,}3\).

Ý nghĩa của nhiều bài tập thở là tăng hàm lượng \(\mathrm{CO_2}\) trong máu bằng cách: nín thở, thả lỏng, làm chậm nhịp thở hoặc tạo “cản” nhẹ khi thở. Khi nồng độ \(\mathrm{CO_2}\) tăng (tới một mức phù hợp, khoảng \(8\%\) theo bài viết), khả năng cơ thể sử dụng \(\mathrm{O_2}\) được cải thiện. Các метод khác nhau đạt điều này bằng: nín thở sau khi hít vào hoặc sau khi thở ra, kéo dài thì thở ra, kéo dài thì hít vào, hoặc kết hợp. Nói cách khác, mục tiêu là làm cho pha thở ra dài hơn đáng kể so với pha hít vào.

Một trong các phương pháp nổi tiếng được nhắc đến là hệ thống Buteyko: thở nông kèm nhịp nín thở. Mục tiêu là giảm “lãng phí” oxy và làm cơ thể “giàu” \(\mathrm{CO_2}\) hơn. (Phần tiếp theo ở trang sau…)

Ví dụ, có kiểu nhịp thở gồm: hít vào \(2\) giây, thở ra \(4\) giây, sau đó là nín thở \(4\) giây. Như vậy, một chu kỳ kéo dài \(10\) giây, tương ứng khoảng \(6\) chu kỳ mỗi phút.

Trong thực hành yoga, người ta thường xem thở ra dài là đúng: tỉ lệ thời gian hít vào và thở ra có thể vào khoảng \(1:5\). Thậm chí có ý kiến cho rằng trong trạng thái thiền sâu, một yogi có thể “đủ dùng” chỉ với khoảng \(2\) chu kỳ hít–thở mỗi phút! Phản ứng đầu tiên thường là: điều đó không thể. Nhưng rồi xuất hiện một gợi ý bất ngờ: nhịp thở cực chậm ở các yogi có thể liên quan đến vai trò lớn hơn của hô hấp qua da.

Hô hấp qua da có “đáng kể” không?

Quả thật, điều này không hẳn là vô lý. Diện tích da người (phủ khoảng 5 triệu sợi lông) vào khoảng \(1{,}5\text{–}2\,\text{m}^2\). Trong khi đó, tổng diện tích bề mặt của khoảng 600 triệu phế nang trong phổi vào khoảng \(100\,\text{m}^2\).

Ước lượng nhanh

Nếu so sánh thô, thì ở mức khoảng \(1\%\text{–}2\%\), da có thể “đóng góp” một phần chức năng hô hấp.

Các phép đo cho thấy: qua da, cơ thể thải ra khoảng \(2\%\) lượng \(\mathrm{CO_2}\) và hấp thụ xấp xỉ \(1\%\) lượng \(\mathrm{O_2}\). Hơn nữa, qua da cơ thể còn thải ra khoảng \(800\,\text{g}\) hơi nước mỗi ngày — thậm chí còn nhiều hơn lượng hơi nước thải qua phổi!

Lời kết

Hít thở sâu không phải “mẹo thần kỳ”, nhưng là một thói quen nhỏ có thể tạo khác biệt lớn — nhất là khi chúng ta sống trong không gian kín, ít thông gió và dễ tích tụ \(\mathrm{CO_2}\). Chỉ cần bạn hiểu cơ thể cần gì và chủ động cải thiện bầu không khí xung quanh, sức khỏe sẽ thay đổi theo hướng tích cực hơn mỗi ngày.

Bạn thường làm gì để không gian sống “dễ thở” hơn: mở cửa sổ theo khung giờ, dùng quạt thông gió, đặt cây xanh, hay có mẹo nào khác? Hãy để lại bình luận để mọi người cùng học hỏi nhé.

Read More

Đề thi học sinh giỏi Vật lý 12 chương trình mới ứng dụng thực tế - Có lời giải chi tiết

Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế – Có lời giải chi tiết là tài liệu ôn luyện dành cho các bạn đang hướng tới kỳ thi học sinh giỏi Vật lý 12 theo định hướng CTPT 2018. Đề được xây dựng bám sát cấu trúc mới, tăng cường các câu hỏi vận dụng thực tiễn giúp học sinh rèn tư duy phân tích hiện tượng và giải quyết vấn đề. Mỗi bài đều có lời giải chi tiết, trình bày rõ ràng theo từng bước để bạn tự học hiệu quả và dễ đối chiếu. Tài liệu phù hợp cho ôn tập HSG cấp trường, cấp tỉnh hoặc luyện đề chọn đội tuyển trong năm học 2025–2026. Hy vọng bộ đề này sẽ giúp bạn củng cố kiến thức trọng tâm, nâng cao kỹ năng làm bài và tự tin đạt kết quả cao trong các kỳ thi sắp tới.

Xem thêm đề tương tự:

• Đề thi HSG Vật lý 12 cấp tỉnh 2024–2025 (Có đáp án)
• Đề chọn đội tuyển HSG Vật lý 12 2025–2026 (Lời giải chi tiết)
• Tuyển tập đề HSG Vật lý 12 CT mới theo chuyên đề

I. Đề thi học sinh giỏi Vật lý 12 chương trình mới ứng dụng thực tế - Có lời giải chi tiết

Câu 1. Vận dụng Chuyển động ném vào thực tế Bắn tên gây mê - Đề thi HSG vật lý 12 chương trình mới ứng dụng thực tế

Một kiểm lâm muốn bắn một mũi tên gây mê vào một con khỉ đang treo mình trên cành cây. Kiểm lâm nhắm thẳng vào con khỉ. Cùng lúc kiểm lâm bắn mũi tên, con khỉ buông cành cây và rơi khỏi cây với vận tốc ban đầu bằng không, hy vọng tránh được mũi tên.

Hình 1. Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế - Kiểm lâm bắn mũi tên gây mê vào con khỉ.

1. Trong ví dụ ở hình, con khỉ ở khoảng cách theo phương ngang $x=20\ \text{m}$ và độ cao $h=12\ \text{m}$, và mũi tên được phóng đi với vận tốc ban đầu $v_0=40\ \mathrm{m/s}$. Khoảng cách liên quan đến vị trí của súng bắn phi tiêu. Xác định:

1. Thời gian để mũi tên bay tới cái cây nơi con khỉ đang ở (ngay phía trên con khỉ).

2. Độ cao mà mũi tên được đặt tại thời điểm đó.

3. Độ cao mà con khỉ đang ở tại thời điểm đó. Lấy $g = 9\text{,}8\ \mathrm{m/s²}$.

2. Chứng minh rằng con khỉ sẽ bị bắn trúng bất kể tốc độ ban đầu của phi tiêu, miễn là tốc độ phi tiêu đủ lớn để di chuyển theo phương ngang đến cây trước khi chạm đất.

Câu 2. Cà kheo bật nhảy - Đề thi HSG vật lý 12 chương trình mới ứng dụng thực tế

Thanh tra Gadget, một nhân vật trong loạt truyện tranh, dùng những chiếc lò xo gắn vào giày để thực hiện các cú nhảy ngoạn mục. Một số vận động viên liều lĩnh cố bắt chước điều này bằng cách sử dụng những chiếc cà kheo do ngành hàng không vũ trụ phát triển, cho phép họ nhảy cao gần $2\ \text{m}$ hoặc “chạy tăng tốc” trên $40\ \text{km/h}$ (Hình 2).

Hình 2. Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế - Cà kheo bật nhảy.

Việc nghiên cứu chi tiết cơ học của các cú nhảy này khá phức tạp. Để đơn giản hóa, ta sẽ dùng một mô hình đơn giản gồm một khối lượng m gắn vào đầu trên của một lò xo lý tưởng, có chiều dài tự nhiên $L_0$ và hằng số đàn hồi $k$. Nếu thả hệ rơi xuống bắt đầu từ độ cao ban đầu $y_0$ (Hình 3), nó sẽ rơi thẳng đứng, chạm đất và bật lên lại. Trong quá trình đi xuống, khối $m$ lần lượt đi qua ba vị trí đặc biệt:

• Đầu dưới của lò xo chạm đất (Hình 4).

• Khối đi qua độ cao $y_\text{eq}$ tại đó tổng lực tác dụng lên nó bằng không (Hình 5). Đây sẽ là độ cao cân bằng của khối nếu hệ được đặt nhẹ nhàng lên mặt đất.

• Khối dừng lại tức thời tại độ cao nhỏ nhất $y_\text{min}$, trước khi bắt đầu đi lên (Hình 6).

Hình 3. Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế - Hệ rơi xuống bắt đầu từ độ cao ban đầu.

Hình 4. Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế - Đầu dưới của lò xo chạm đất.

Hình 5. Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế - Hệ rơi xuống bắt đầu từ độ cao ban đầu.

Hình 6. Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế - Khối dừng lại tức thời tại độ cao nhỏ nhất.

Giả sử đã biết $L_0$, $y_\text{ini}$, $y_\text{min}$ và gia tốc trọng trường $g$. Hãy trả lời các câu hỏi sau, biểu diễn kết quả theo các dữ kiện đã cho:

1. Xác định tỉ số $\dfrac{k}{m}$ giữa độ cứng của lò xo và khối lượng của khối.

2. Xác định độ cao của vị trí cân bằng $y_\text{eq}$.

3. Mô tả gia tốc của $m$ trong các khoảng sau:

1. Từ $y=y_\text{ini}$ đến $y=L_0$.

2. Từ $y=L_0$ đến $y=y_\text{min}$.

4. Trong lúc rơi, gia tốc của khối đạt cực đại tại độ cao $y_1$ nào? Giá trị đó là bao nhiêu, $a_\text{max}$?

Cho hai câu tiếp theo, dùng dữ liệu số:
$L_0=80\ \text{cm}$, $y_\text{ini} =2\text{,}0\ \text{m}$, $y_\text{min}=20\ \text{cm}$, $g=9\text{,}8\ \mathrm{m/s^2}$.

5. Tính các giá trị $\dfrac{k}{m}$, $y_\text{eq}$ và $a_\text{max}$.

6. Vẽ đồ thị biểu diễn $\dfrac{a}{g}$ theo $y$, trong khoảng $y_\text{min}≤y≤y_\text{ini}$.

Câu 3. Chu trình nhiệt - Đề thi HSG vật lý 12 chương trình mới ứng dụng thực tế

Một khí đơn nguyên tử lý tưởng chuyển từ trạng thái 1, tại đó nhiệt độ là $T_1=300\ \text{K}$, sang trạng thái 2 có nhiệt độ $T_2$ bằng một quá trình trong đó áp suất khí tăng tỉ lệ thuận với thể tích (Hình 7). Trong quá trình này, áp suất khí tăng $k = 2$ lần. Quá trình 2-3 là đẳng nhiệt, trong quá trình 3-4, áp suất tỉ lệ thuận với thể tích, quá trình 4-1 là đẳng nhiệt. Thể tích ở trạng thái 2 và 4 là như nhau.

Hình 7. Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế - Đồ thị chu trình nhiệt.

1. Xác định nhiệt độ $T_2$ trong quá trình 2-3.

2. Mối quan hệ giữa áp suất $p_1$ và $p_3$ là gì?

3. Nhiệt dung mol của khí $C$ trong quá trình 1-2 là bao nhiêu? (Có thể chứng minh rằng đối với các quá trình trong đó áp suất tỉ lệ thuận với thể tích, nhiệt dung là không đổi). Hiệu suất của quá trình tuần hoàn này là bao nhiêu?

Câu 4. Một món đồ chơi bất ngờ: máy phát Van de Graaff

Trong các phòng thí nghiệm ở các trường phổ thông, bộ thí nghiệm về tĩnh điện phổ biến nhất là bộ tích điện cho một quả cầu kim loại, thường gọi là máy phát Van de Graaff. Thiết bị này dùng cơ cấu cơ học để nạp dần điện tích Q lên quả cầu, nhờ đó tạo ra điện trường rất mạnh ở vùng không gian xung quanh, giúp quan sát rõ tác dụng của điện trường và lực điện.
Một thí nghiệm điển hình là nạp điện từ từ cho quả cầu cho đến khi xuất hiện một tia lửa điện rất ngoạn mục (Hình 8). Quả cầu tích điện gây ra điện trường xung quanh nó. Khi điện tích đủ lớn, cường độ điện trường mạnh đến mức ion hóa các phân tử không khí, tạo ra một dòng điện đột ngột kèm theo sự phát sáng nhìn thấy được do các điện tích tự do va chạm với các phân tử không khí khác. Cường độ điện trường lớn nhất mà không khí chịu được trước khi bị ion hóa, là $E_{\max}=3\cdot10^6\,\text{V/m}$.

Hình 8. Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế - Tia lửa điện phóng ra từ quả cầu tích điện.

1. Hãy xác định điện tích cực đại $Q_{\max}$ có thể cung cấp cho một quả cầu Van de Graaff bán kính $R=10\,\text{cm}$, để không xảy ra đánh thủng điện môi của không khí xung quanh (cường độ điện trường bên ngoài quả cầu giống hệt như cường độ điện trường do một điện tích điểm đặt tại tâm quả cầu, mang cùng điện tích với quả cầu).

Một thí nghiệm khác có thể làm với Van de Graaff là đặt lên đỉnh quả cầu một cái cốc nhôm. Cốc nhôm cũng được tích điện cùng dấu với quả cầu. Người ta quan sát thấy điện trường hất cốc bay lên khỏi bề mặt quả cầu.

Hình 9. Đề thi HSG Vật lý 12 chương trình mới ứng dụng thực tế - Cốc nhôm bị quả cầu hất tung lên.

Việc nghiên cứu chính xác chuyển động của cốc nhôm này khá phức tạp. Để có thể tính gần đúng, ta đưa ra một vài giả thiết:

• Khi cốc nhôm tách khỏi quả cầu, nó mang đi một phần điện tích của hệ, nhưng máy phát gần như ngay lập tức bù lại đúng lượng điện tích đó cho quả cầu, nên điện tích của quả cầu được giữ không đổi.

• Cốc nhôm nhỏ hơn rất nhiều so với quả cầu và có thể coi như điện tích điểm.

• Điện trường của qua cầu tích điện Q luôn giống như điện trường của điện tích điểm Q đặt ở tâm của nó.

• Bỏ qua lực cản/ma sát của không khí, lấy $g=9\text{,}8\ \mathrm{m/s^2}$.

• Khi cốc nhôm bật lên, nó chuyển động theo đường thẳng đứng.

• Công của lực điện thực hiện khi điện tích điểm q di chuyển từ khoảng cách $r_1$ đến khoảng cách $r_2$ tính từ tâm quả cầu là $A=kQq\left(\dfrac{1}{r_1} -\dfrac{1}{r_2}\right)$.

Giả sử quả cầu được nạp đến điện tích $Q_0=2{,}5\ \text{μC}$, trên nó đặt một cốc nhôm duy nhất có khối lượng $m=3{,}0\ \text{g}$ và điện tích $q=7{,}5×10^{-2}\ \text{μC}$, hãy xác định:

2. Gia tốc của cốc khi bắt đầu tách khỏi bề mặt quả cầu.

3. Khoảng cách lớn nhất $r_\text{max}$ từ tâm quả cầu mà cốc nhôm đạt tới. c

4. Khoảng cách $r_{v_\text{max}}$ từ tâm quả cầu đến điểm mà tốc độ của cốc nhôm đạt cực đại.

5. Giá trị của tốc độ lớn nhất $v_\text{max}$ mà cốc nhôm đạt được.

Câu 5. Giao thoa ánh sáng - Đề thi HSG Vật lý 12 mới nhất theo hướng ứng dụng thực tế

Trong thí nghiệm Young về giao thoa ánh sáng, nguồn sáng phát ra ánh sáng đơn sắc có bước sóng $λ_1$. Trên màn quan sát, trên đoạn thẳng MN dài $20\ \text{mm}$ (MN vuông góc với hệ vân giao thoa) có $10$ vân tối, M và N là vị trí của hai vân sáng.

1. Khoảng cách từ màn quan sát đến hai khe gấp bao nhiêu lần khoảng cách giữa hai khe?

2. Thay ánh sáng trên bằng ánh sáng đơn sắc có bước sóng $λ_2=\dfrac{5λ_1}{3}$ thì tại M là vị trí của một vân sáng giao thoa, số vân sáng trên đoạn MN lúc này bằng bao nhiêu?

Read More

Giải các bài toán Vật lý bằng phương pháp quy nạp

Mục lục

1. Giới thiệu về phương pháp quy nạp và việc giải các bài toán Vật lý bằng phương pháp quy nạp
2. Hệ thống các bài toán Vật lý được giải bằng phương pháp quy nạp
• Bài toán 1. Tàu tăng tốc – thời gian toa thứ n
• Bài toán 2. Vật rơi trong khe – số lần va chạm
• Bài toán 3. Bóng nảy trên mặt phẳng nghiêng
• Bài toán 4. Tâm khối thanh gắn dãy khối lượng
• Bài toán 5. Bơm pít-tông – áp suất sau n lần
• Bài toán 6. Mạng điện trở n nút – điện trở tương đương
• Bài toán 7. Nạp tụ nối tiếp – điện áp cực đại
• Bài toán 8. Tường cách âm – độ dày cần thiết
3. Các bài tập tự giải bằng phương pháp quy nạp

Giới thiệu về phương pháp quy nạp và việc giải các bài toán Vật lý bằng phương pháp quy nạp

Giải các bài toán Vật lý bằng phương pháp quy nạp là cách tiếp cận giúp người học tìm quy luật nhanh, khái quát công thức tổng quát và nâng cao tư duy giải bài tập Vật lý thông qua việc phân tích nhiều trường hợp riêng rồi suy ra kết luận cho trường hợp tổng quát. Trong nghiên cứu khoa học và học tập về thế giới xung quanh, phương pháp dựa trên các suy luận quy nạp được sử dụng rộng rãi. Phương pháp này được gọi là phương pháp quy nạp và thuộc về các phương pháp nghiên cứu khoa học chung. Thuật ngữ «quy nạp» (lat. inductio) có nghĩa là «dẫn đến», còn các kết luận quy nạp là những kết luận được rút ra dựa trên quan sát và thực nghiệm, tức là thu được bằng cách xem xét các trường hợp riêng lẻ và sau đó mở rộng những quy luật đã nhận thấy sang trường hợp tổng quát. Vai trò của phương pháp quy nạp đặc biệt quan trọng trong Vật lý thực nghiệm. Tuy nhiên, phương pháp quy nạp cũng tỏ ra hữu ích khi giải bài tập Vật lý trong chương trình học. Bằng suy luận quy nạp, người ta xác lập được một quy luật hoặc một công thức nào đó trên cơ sở khái quát hóa kết quả của ba hoặc nhiều trường hợp riêng lẻ.

Dưới đây là một số bài toán Vật lý hay mà trong đó quy nạp được xem như một phương pháp heuristic (gợi tìm) để giải, giúp bạn nhận dạng dạng bài, rút gọn lập luận và trình bày lời giải mạch lạc. Không loại trừ khả năng những bài toán này còn có các cách giải khác.

Hệ thống các bài toán Vật lý được giải bằng phương pháp quy nạp

Bài toán 1. Tàu tăng tốc – thời gian toa thứ $n$

Một người quan sát đứng tại mép trước của đoàn tàu điện ngay tại thời điểm bắt đầu chuyển động, nhận thấy rằng toa thứ nhất đi qua ông trong thời gian \( t_1 = 4\,\text{s} \). Hỏi toa thứ mười sẽ đi qua ông trong thời gian bao lâu? Chuyển động được coi là chuyển động nhanh dần đều.

Lời giải (Bài toán 1)

Chiều dài của toa thứ nhất

\[ L = \frac{a t_1^2}{2}, \]

còn của toa thứ hai

\[ L = v_1 t_2 + \frac{a t_2^2}{2}, \]

trong đó

\[ v_1 = a t_1. \]

Ở đây \( v_1 \) là vận tốc của mép trước toa thứ hai khi nó đi ngang qua người quan sát, \( t_2 \) là thời gian mà toa thứ hai đi qua người quan sát. Rõ ràng rằng

\[ \frac{a t_1^2}{2} = a t_1 t_2 + \frac{a t_2^2}{2} \]

và

\[ t_2 = t_1(\sqrt{2} - \sqrt{1}). \]

Đối với toa thứ ba

\[ L = v_2 t_3 + \frac{a t_3^2}{2}, \]

trong đó

\[ v_2 = v_1 + a t_2 = a(t_1 + t_2). \]

Do đó,

\[ t_3^2 + 2(t_1 + t_2)t_3 - t_1^2 = 0, \]

\[ t_3 = t_1(\sqrt{3} - \sqrt{2}). \]

Đối với toa thứ tư, ta nhận được

\[ t_4 = t_1(\sqrt{4} - \sqrt{3}). \]

Dựa trên suy luận quy nạp từ các biểu thức đối với \( t_1, t_2, t_3 \) và \( t_4 \), ta tìm được quy luật sau cho \( t_n \):

\[ t_n = t_1(\sqrt{n} - \sqrt{n-1}). \]

Vậy,

\[ t_{10} = 4\,\text{s}(\sqrt{10} - \sqrt{9}) \approx 0{,}65\,\text{s}. \]

Bài toán 2. Vật rơi trong khe – số lần va chạm

Một vật nhỏ đàn hồi trượt với vận tốc \( v_0 = 10\,\text{m/s} \) trên một mặt phẳng nằm ngang, tiến gần đến một khe hở (xem Hình vẽ 1). Khe được tạo thành bởi hai vách song song thẳng đứng, cách nhau một khoảng \( d = 5\,\text{cm} \). Độ sâu của khe \( H = 1\,\text{m} \). Hãy xác định vật sẽ va chạm vào các vách bao nhiêu lần trước khi chạm đáy. Các va chạm với vách là hoàn toàn đàn hồi. Lấy \( g = 9{,}8\,\text{m/s}^2 \).

Hình vẽ 1

Lời giải (Bài toán 2)

Khi va chạm đàn hồi với các vách của khe, góc phản xạ bằng góc tới, và thời gian bay của vật giữa các vách \( t \) là không đổi và bằng

\[ t = \frac{d}{v_0}. \]

Va chạm thứ nhất xảy ra ở độ sâu

\[ h_1 = v_{y1} t + \frac{g t^2}{2}, \]

va chạm thứ hai — ở độ sâu

\[ h_2 = v_{y2} t + \frac{g t^2}{2} \]

tính từ điểm va chạm thứ nhất,

va chạm thứ ba — ở độ sâu

\[ h_3 = v_3 t + \frac{g t^2}{2} \]

tính từ điểm va chạm thứ hai, v.v. Dựa trên suy luận quy nạp, ta viết các giá trị sau của các thành phần thẳng đứng của vận tốc của vật:

\[ v_1 = 0,\; v_2 = g t,\; v_3 = 2 g t,\; \ldots,\; v_n = (n-1) g t, \]

trong đó \(n\) là số thứ tự của va chạm. Hiển nhiên rằng

\[ h_1 + h_2 + \ldots + h_n = H, \]

hay

\[ (v_1 + v_2 + \ldots + v_n)t + n\frac{g t^2}{2} = H. \]

Tiếp theo, lần lượt ta có

\[ (g + 2 g t + 3 g t + \ldots + (n-1) g t)t + n\frac{g t^2}{2} = H, \]

\[ g t^2(1 + 2 + 3 + \ldots + (n-1)) + n\frac{g t^2}{2} = H, \]

\[ \ldots \]

\[ \frac{g t^2}{2}n(n-1) + n\frac{g t^2}{2} = H. \]

Từ đó suy ra

\[ n = \sqrt{\frac{2H}{g t^2}} = \frac{v_0}{d}\sqrt{\frac{2H}{g}} \approx 90{,}3. \]

Vì số lần va chạm là một số tự nhiên, nên \(n = 90\). Vật sẽ va vào các vách của khe \(90\) lần.

Bài toán 3. Bóng nảy trên mặt phẳng nghiêng

Quả bóng rơi tự do từ độ cao \( h = 0{,}1\,\text{m} \) xuống một tấm ván nghiêng tạo với phương ngang góc \( \alpha = 30^\circ \). Quả bóng, khi nảy lên, chuyển động dọc theo tấm ván (Hình vẽ 2). Hãy tìm khoảng cách giữa điểm va chạm thứ chín và thứ mười của quả bóng với tấm ván. Các va chạm của bóng với tấm ván là hoàn toàn đàn hồi.

Hình vẽ 2

Lời giải (Bài toán 3)

Ta tìm khoảng cách giữa các điểm va chạm thứ nhất và thứ hai \((L_{1,2})\), thứ hai và thứ ba \((L_{2,3})\), thứ ba và thứ tư \((L_{3,4})\). Để thuận tiện, chọn trục tọa độ dọc theo tấm ván và vuông góc với nó (Hình vẽ 3).

Hình vẽ 3

Trong trường hợp này, các hình chiếu gia tốc của quả bóng lên các trục \(x\) và \(y\) sẽ lần lượt bằng

\[ a_x = g_x = g\sin\alpha \quad \text{và} \quad a_y = g_y = -g\cos\alpha. \]

Vận tốc của bóng tại thời điểm va chạm đầu tiên với tấm ván bằng

\[ v_0 = \sqrt{2gh}. \]

Vận tốc ban đầu của bóng sau va chạm thứ nhất bằng \(v_0\) và tạo với trục \(y\) một góc \(\alpha\), còn các hình chiếu của vận tốc của bóng bằng

\[ v_{0x} = v_0\sin\alpha \quad \text{và} \quad v_{0y} = v_0\cos\alpha. \]

Khoảng cách giữa các điểm va chạm thứ nhất và thứ hai của bóng với tấm ván bằng

\[ L_{1,2} = (v_0\sin\alpha)t_1 + \frac{(g\sin\alpha)t_1^2}{2}, \]

trong đó \(t_1\) là thời gian bay của bóng. Thời gian này được xác định bởi phương trình

\[ (v_0\cos\alpha)t_1 - \frac{(g\cos\alpha)t_1^2}{2} = 0. \]

Từ đó

\[ t_1 = \frac{2v_0}{g} \quad \text{và} \quad L_{1,2} = 8h\sin\alpha. \]

Vận tốc của bóng tại thời điểm va chạm thứ hai được xác định bởi các đẳng thức

\[ v_{1x} = v_{0x} + a_x t_1 = v_0\sin\alpha + (g\sin\alpha)t_1 = 3v_0\sin\alpha, \]

\[ v_{1y} = v_{0y} + a_y t_1 = v_0\cos\alpha - (g\cos\alpha)t_1 = -v_0\cos\alpha. \]

Sau va chạm thứ hai, các vận tốc này bằng

\[ v_{2x} = v_{1x}, \quad v_{2y} = -v_{1y} = v_0\cos\alpha = v_{0y}. \]

Khoảng cách giữa các điểm va chạm thứ hai và thứ ba bằng

\[ L_{2,3} = (3v_0\sin\alpha)t_2 + \frac{(g\sin\alpha)t_2^2}{2}, \]

trong đó \(t_2\) là thời gian bay. Vì vận tốc ban đầu theo trục \(y\) giống như ở va chạm thứ nhất, nên \(t_2 = t_1\). Do đó

\[ L_{2,3} = 16h\sin\alpha. \]

Tương tự có thể chỉ ra rằng

\[ L_{3,4} = 24h\sin\alpha. \]

Dựa trên phương pháp quy nạp, ta viết

\[ L_{n,n+1} = 8nh\sin\alpha. \]

Suy ra,

\[ L_{9,10} = 8\cdot 9\cdot 0{,}1\,\text{m}\cdot \sin 30^\circ = 3{,}6\,\text{m}. \]

Bài toán 4. Tâm khối thanh gắn dãy khối lượng

Hãy tìm vị trí của tâm khối của một thanh không trọng lượng với các quả cầu gắn trên nó (xem Hình vẽ 4).

Hình vẽ 4

Lời giải (Bài toán 4)

… với các quả cầu (xem Hình vẽ 4). Khoảng cách giữa các tâm của các quả cầu là

\[ d = 10\,\text{cm}, \]

khối lượng các quả cầu tạo thành một cấp số cộng

\[ 1,\;2,\;3,\;\ldots,\;100\,\text{kg}. \]

Trước hết xét hai quả cầu có khối lượng \(1\,\text{kg}\) và \(2\,\text{kg}\). Tâm khối của hệ như vậy nằm cách đầu nhẹ của thanh một khoảng bằng hai phần ba chiều dài thanh:

\[ L_2=\frac{2}{3}d. \]

Tiếp theo, tính vị trí tâm khối đối với ba quả cầu có khối lượng \(1\,\text{kg}\), \(2\,\text{kg}\) và \(3\,\text{kg}\):

\[ L_3=\frac{4}{3}d \]

và đối với bốn quả cầu có khối lượng \(1\,\text{kg}\), \(2\,\text{kg}\), \(3\,\text{kg}\) và \(4\,\text{kg}\):

\[ L_4=\frac{6}{3}d. \]

Dựa trên phương pháp quy nạp, đối với \(n\) quả cầu ta viết vị trí tâm khối của thanh dưới dạng tổng quát:

\[ x_n=\frac{2(n-1)}{3}d. \]

Do đó, vị trí tâm khối của thanh không trọng lượng với \(100\) quả cầu gắn trên nó nằm tại điểm có tọa độ

\[ L_{100}=\frac{2\cdot 99}{3}\cdot 10\,\text{cm} = 660\,\text{cm}. \]

Bài toán 5. Bơm pít-tông – áp suất sau $n$ lần

Một bơm pít-tông, trong mỗi lần bơm, hút vào một thể tích không khí \(V_0\). Khi pít-tông bắt đầu chuyển động từ trái sang phải, van \(a\) mở và một phần khối lượng không khí đi vào xi lanh của pít-tông. Khi chuyển động từ phải sang trái, van \(a\) đóng và van \(b\) mở, qua đó khí đi vào hệ thống.

Hình vẽ 5

Khi bơm bằng bơm này, không khí từ bình có thể tích \(V\) đã được bơm \(n\) lần. Hãy tìm áp suất thiết lập trong bình, trong đó áp suất ban đầu trong bình là \(p_0\). Quá trình là đẳng nhiệt.

Lời giải (Bài toán 5)

Sau một lần bơm, áp suất trong bình sẽ bằng

\[ p_1=\frac{p_0V}{V+V_0}, \]

sau lần bơm thứ hai

\[ p_1V=p_2(V+V_0) \]

và do đó,

\[ p_2=\frac{p_0V}{(V+V_0)^2}, \]

sau lần thứ ba, áp suất sẽ là

\[ p_3=\frac{p_0V}{(V+V_0)^3}. \]

Sau \(n\) lần bơm, áp suất trong bình sẽ là

\[ p_n=\frac{p_0V}{(V+V_0)^n}. \]

Bài toán 6. Mạng điện trở n nút – điện trở tương đương

Có \(20\) kẹp, mỗi kẹp được nối với tất cả các kẹp còn lại thông qua các điện trở giống nhau, điện trở của mỗi cái bằng \(10\,\text{Ohm}\). Hãy tìm điện trở giữa bất kỳ hai kẹp nào.

Lời giải (Bài toán 6)

Ban đầu lấy hai kẹp, tức là \(n=2\) (Hình vẽ 6,a). Điện trở giữa chúng

\[ R_2=R. \]

Tiếp theo lấy ba kẹp (Hình vẽ 6,b). Điện trở giữa các kẹp \(1\) và \(2\) bằng

\[ R_3=\frac{2R}{3}. \]

Hình vẽ 6

Lấy bốn kẹp (Hình vẽ 6,c). Nối nguồn dòng điện vào các kẹp \(1\) và \(2\). Vì tại các điểm \(3\) và \(4\) các thế là như nhau, nên qua điện trở nối hai kẹp này sẽ không có dòng điện chạy. Do đó, có thể bỏ nó đi. Như vậy,

\[ R_4=\frac{R}{2}=\frac{2R}{4}. \]

Kết quả tổng quát (Bài toán 6)

\[ R_2=\frac{2R}{2},\quad R_3=\frac{2R}{3},\quad R_4=\frac{2R}{4}, \]

ta tìm được công thức tổng quát cho điện trở giữa bất kỳ hai kẹp nào:

\[ R_n=\frac{2R}{n}\quad (n>2). \]

Vậy,

\[ R_{20}=\frac{2\cdot 10\,\text{Ohm}}{20}=1\,\text{Ohm}. \]

Bài toán 7. Nạp tụ nối tiếp – điện áp cực đại

Một tụ điện có điện dung \( C_0=20\,\text{mkF} \) được nạp đến hiệu điện thế \( U_0=400\,\text{V} \) và nối với một tụ điện có điện dung \( C=1\,\text{mkF} \), kết quả là tụ sau được nạp điện. Ngắt tụ này ra, rồi nạp tụ thứ hai theo cách tương tự (cũng có điện dung \( C=1\,\text{mkF} \)), tụ thứ ba, v.v. Sau đó nối các tụ điện lại nối tiếp. Hỏi có thể thu được hiệu điện thế cực đại nào theo cách này?

Lời giải (Bài toán 7)

Điện tích ban đầu của tụ ban đầu

\[ q_0=C_0U_0. \]

Sau khi nối tụ thứ nhất, điện tích \(q_0\) sẽ phân bố giữa hai tụ có điện dung \(C_0\) và \(C\). Sau khi tách ra, trên cả hai tụ sẽ thiết lập hiệu điện thế

\[ U_1=\frac{q_0}{C_0+C}=\frac{C_0U_0}{C_0+C}. \]

Điện tích còn lại trên tụ có điện dung \(C_0\) bằng

\[ q_1=C_0U_1=\frac{C_0^2U_0}{C_0+C}. \]

Khi nạp tụ thứ hai, điện áp trên cả hai tụ (có điện dung \(C_0\) và \(C\)) trở thành

\[ U_2=\frac{q_1}{C_0+C}=U_0\left(\frac{C_0}{C_0+C}\right)^2, \]

và sau khi nối tụ thứ ba —

\[ U_3=U_0\left(\frac{C_0}{C_0+C}\right)^3. \]

Rõ ràng,

\[ U_n=U_0\left(\frac{C_0}{C_0+C}\right)^n. \]

Tiếp theo, ta viết công thức cho hiệu điện thế cực đại dưới dạng tổng vô hạn của một cấp số nhân giảm:

\[ U=U_1+U_2+U_3+\ldots+U_n= \]

\[ =U_0\left(\frac{C_0}{C_0+C}+\left(\frac{C_0}{C_0+C}\right)^2+\left(\frac{C_0}{C_0+C}\right)^3+\ldots+\left(\frac{C_0}{C_0+C}\right)^n\right). \]

Cộng cấp số nhân này, ta được

\[ U=\frac{C_0U_0}{C}=8000\,\text{V}. \]

Bài toán 8. Tường cách âm – độ dày cần thiết

Cường độ âm thanh (tiếng ồn) phía sau bức tường là \(10\,\text{W/m}^2\) (ngưỡng gây cảm giác đau). Tường được làm bằng vật liệu hấp thụ âm. Tường phải dày bao nhiêu để trong phòng còn lại mức cường độ âm cho phép là \(10^{-10}\,\text{W/m}^2\), nếu cường độ âm qua mỗi \(1\,\text{mm}\) vật liệu giảm đi \(10\%\)?

Lời giải (Bài toán 8)

Hãy tưởng tượng chia tường thành các lớp dày \(1\,\text{mm}\). Sau khi đi qua lớp thứ nhất, cường độ âm là

\[ I_1=I_0(1-\beta), \]

trong đó

\[ I_0=10\,\text{W/m}^2,\quad \beta=0{,}1. \]

Tương tự, sau khi đi qua lớp thứ hai

\[ I_2=I_1(1-\beta)=I_0(1-\beta)^2, \]

sau khi đi qua lớp thứ ba

\[ I_3=I_2(1-\beta)=I_0(1-\beta)^3. \]

Khi đó đối với lớp thứ \(n\)

\[ I_n=I_0(1-\beta)^n. \]

Từ đây

\[ n=\frac{\lg\left(\frac{I_n}{I_0}\right)}{\lg(1-\beta)}=\frac{\lg 10^{-11}}{\lg(1-0{,}1)}\approx 240. \]

Như vậy, độ dày cần tìm của bức tường bằng

\[ 240\,\text{mm}. \]

Các bài tập tự giải bằng phương pháp quy nạp

1. Trong thời gian bao lâu một vật rơi tự do không có vận tốc ban đầu đi hết mét thứ mười của quãng đường rơi?
2. Có một mạch điện chứa \(10\) tiếp điểm. Mỗi cặp tiếp điểm được nối với nhau qua một tụ điện có điện dung \(10\,\text{mkF}\). Khi đo giữa hai tiếp điểm bất kỳ, sẽ phát hiện điện dung tương đương bằng bao nhiêu?

Lời kết

Qua loạt ví dụ trên, bạn có thể thấy Giải các bài toán Vật lý bằng phương pháp quy nạp không chỉ là một “mẹo giải nhanh”, mà còn là cách rèn tư duy tìm quy luật, khái quát công thức tổng quát và nhìn ra cấu trúc của bài toán từ vài trường hợp đầu. Khi đã quen, bạn sẽ xử lý tốt nhiều dạng bài quen thuộc như chuyển động nhanh dần đều, va chạm đàn hồi, tâm khối, mạch điện đối xứng, cấp số nhân trong tụ điện và cả suy giảm cường độ âm.

Nếu bạn muốn mình phát triển bài viết này thành một “chuỗi” dễ học hơn, hãy để lại bình luận: bạn thấy Bài toán số mấy hay/khó nhất? và bạn muốn thêm dạng bài nào (cơ học, điện xoay chiều, quang học, nhiệt học…). Mình cũng có thể làm thêm phần bài tập tự luyện + đáp án theo đúng tinh thần quy nạp để bạn luyện kỹ năng nhận dạng quy luật.

Nếu bạn thấy bài viết hữu ích, hãy chia sẻ cho bạn bè đang học Vật lý và lưu lại để dùng khi ôn thi. Bạn có câu hỏi nào cần mình giải theo phương pháp quy nạp không? Cứ gửi đề ngay dưới phần bình luận nhé!

↑ Lên đầu trang

Read More

Chuyển động của các thiên thể trong trường hấp dẫn

Chuyển động của các thiên thể trong trường hấp dẫn là một mảng kiến thức cốt lõi của cơ học thiên thể và cũng là chủ đề “ăn điểm” trong các chuyên đề ôn thi Học sinh giỏi Vật lí. Những năm gần đây, đề thi HSG Quốc gia môn Vật lí thường xuyên xuất hiện các câu hỏi về chuyển động trong trường hấp dẫn (vệ tinh, hành tinh, tàu vũ trụ), yêu cầu học sinh nắm vững định luật vạn vật hấp dẫn, vận dụng thành thạo các định luật động lực học và suy ra các hệ quả kinh điển như các định luật Kepler. Bài viết này được biên tập theo hướng chuyên đề bồi dưỡng học sinh giỏi Vật lí: hệ thống hoá các tích phân chuyển động (bảo toàn mômen động lượng, “tích phân diện tích”/Kepler II và tích phân năng lượng), đồng thời tổng hợp chuỗi bài toán chọn lọc về quỹ đạo elip–hypebol, rơi vệ tinh, chuyển quỹ đạo và bay sượt hấp dẫn (gravity assist). Nội dung phù hợp để giáo viên dùng khi ra đề – chữa đề, và giúp học sinh rèn kĩ năng biến đổi nhanh cho các kì thi HSG Quốc gia, khu vực, Quốc tế và Olympic Vật lí.

Bài viết được trình bày theo mục lục sau đây:

• I. Kiến thức trọng tâm về chuyển động của các thiên thể trong trường hấp dẫn
  • 1. Trường xuyên tâm & mômen động lượng (Kepler II)
  • 2. Tích phân năng lượng & vận tốc quỹ đạo
  • 3. Cận tâm – viễn tâm, Viète, bán trục lớn
  • 4. Kepler III và hệ hai vật
  • 5. Quỹ đạo elip/hypebol và tham số $a,e,p,b$
• II. Hệ thống bài toán về chuyển động của các thiên thể trong trường hấp dẫn
  • Bài toán 1. Dòng hạt bụi vũ trụ – bắt giữ hấp dẫn
  • Bài toán 2. Vệ tinh hãm tốc – thời gian rơi
  • Bài toán 3. Mô-đun rơi xuống Mặt Trăng – vận tốc tách
  • Bài toán 4. Năng lượng tối thiểu để thoát trường hấp dẫn
  • Bài toán 5. Chuyển quỹ đạo Trái Đất → Sao Thổ (Hohmann)
  • Bài toán 6. Quỹ đạo cận nhật $0.01$ AU – góc bẻ & vận tốc phóng
  • Bài toán 7. Bay sượt hành tinh – $r_{\min}$ và góc lệch $\varphi$
  • Bài toán 8. Vượt vận tốc cấp ba – $v_k$ và góc tiệm cận $\alpha$
  • Bài toán 9. Gravity assist Sao Hỏa – độ lệch tâm & năng lượng pin
• III. Bài tập tự giải

I. Kiến thức trọng tâm về chuyển động của các thiên thể trong trường hấp dẫn

1. Trường lực xuyên tâm và bảo toàn mômen động lượng (tích phân diện tích – Kepler II)

Ta xét một vài khái quát và hệ quả then chốt làm nền tảng cho mô tả chuyển động trong trường lực trung tâm. Khi hai vật tương tác hấp dẫn, tâm khối của chúng được coi là tâm hút và gắn với nó một “cực”, tức gốc của vectơ bán kính mô tả chuyển động. Khi khối lượng hai vật chênh lệch nhau nhiều bậc, người ta coi tâm hút là tâm khối của vật lớn, và hệ quy chiếu gắn với nó là quán tính. Lực hấp dẫn tác dụng lên vật thứ hai và vectơ bán kính mô tả chuyển động của nó là hai vectơ cùng phương. Tích có hướng của chúng (mômen lực) bằng không. Theo phương trình động lực học quay, mômen động lượng của vật thứ hai đối với tâm hút là đại lượng bảo toàn:

$$\begin{align} \vec{M} &= \vec{r}\times\vec{F}=0,\\ \vec{M} &= \frac{d\vec{L}}{dt}=0. \end{align}$$

$$\begin{align} \vec{L} &= \vec{r}\times m\vec{v}=\text{const},\\ \vec{r}\times\vec{v} &= \text{const}. \end{align}$$

Người ta gọi $\vec{r}\times\vec{v}=\vec{s}_0$ là tốc độ quét diện tích (tốc độ “sector”), trong đó $s_0=2S_t$, với $S_t$ là diện tích mà vectơ bán kính quét được trong mỗi giây đối với một vật chuyển động trong trường lực trung tâm. Tính không đổi của $s_0$ chính là nội dung của định luật Kepler thứ hai. Cách suy luận trên được gọi là tích phân diện tích. Thực chất, nó biểu diễn định luật bảo toàn mômen động lượng, vì $L=2mS_t$.

Nếu đưa vào tham số ngắm (tham số va chạm) $b=r\sin\alpha$, tức độ dài đoạn vuông góc kẻ từ tâm hút đến phương của vectơ xung lượng, thì kết quả của ta ở dạng vô hướng cho hai điểm trên quỹ đạo sẽ là:

$$\begin{align} v_0b_0 &= v_1b_1 = 2S_t = \text{const}. \end{align}$$

2. Tích phân năng lượng và hệ thức vận tốc trên quỹ đạo

Tính bảo toàn (trường thế) của trường hấp dẫn cho phép đưa vào đặc trưng năng lượng của trường và thêm một tích phân chuyển động nữa — tích phân năng lượng. Ta nhân từng vế phương trình động lực học cơ bản cho trường hấp dẫn $m\dfrac{dv}{dt}=\dfrac{GMm}{r^2}$ với $v=\dfrac{dr}{dt}$ và biến đổi. Kết quả thu được:

$$\begin{align} \frac{d}{dt}\left(\frac{v^2}{2}-\frac{GM}{r}\right) &= 0,\\ \frac{v^2}{2}-\frac{GM}{r} &= E_0=\text{const}. \end{align}$$

Số hạng thứ hai biểu thị thế năng của một đơn vị khối lượng trong trường hấp dẫn, tức thế hấp dẫn, còn toàn bộ biểu thức là định luật bảo toàn năng lượng. Ở dạng quen thuộc, cho hai điểm trên quỹ đạo có thể viết:

$$\frac{mv_1^2}{2}-\frac{GMm}{r_1}=\frac{mv_2^2}{2}-\frac{GMm}{r_2}.$$

Năng lượng toàn phần của một đơn vị khối lượng quyết định dạng quỹ đạo. Với quỹ đạo elip có bán trục lớn $a$, ta có:

$$E_0=-\frac{GM}{2a}.$$

Khi đó tích phân năng lượng nhận dạng:

$$v^2=GM\left(\frac{2}{r}-\frac{1}{a}\right).$$

3. Cận tâm – viễn tâm, hệ thức Viète và ý nghĩa bán trục lớn

Hệ thức ngay trên đây liên hệ vận tốc của vật tại khoảng cách $r$ đến tâm hút với bán trục lớn $a$ của quỹ đạo và được dùng rất rộng rãi khi tính toán quỹ đạo. Ở đây đã nêu cách chứng minh năng lượng toàn phần của một đơn vị khối lượng trên quỹ đạo elip, sử dụng cả hai tích phân chuyển động. Tích phân diện tích sẽ được viết cho các điểm cận tâm tại cận tâm và viễn tâm, khi vận tốc vuông góc với vectơ bán kính:

$$\begin{align} v_1r_1 &= v_2r_2 = S,\\ v &= \frac{S}{r}. \end{align}$$

$$\frac{v^2}{2}-\frac{GM}{r}=E_0,\qquad r^2+\frac{GM}{E_0}\,r-\frac{S^2}{2E_0}=0.$$

Hai nghiệm của phương trình sau cùng tương ứng với khoảng cách đến viễn tâm và cận tâm $r_1$ và $r_2$. Tổng các khoảng cách này:

$$r_1+r_2=2a,$$

trong đó $a$ là bán trục lớn của quỹ đạo. Nhưng theo định lý Viète, $r_1+r_2=-\dfrac{GM}{E_0}$. Do đó

$$E_0=-\frac{GM}{2a}$$

là năng lượng cơ học toàn phần của một đơn vị khối lượng trong trường hấp dẫn đối với quỹ đạo elip.

4. Định luật Kepler III và dạng tổng quát cho hệ hai vật

Phương trình động lực học cơ bản và định luật vạn vật hấp dẫn cũng suy ra định luật Kepler thứ ba. Với quỹ đạo tròn, việc này khá đơn giản. Thật vậy,

$$\begin{align} m\,a_{\text{ht}} &= \frac{GMm}{r^2},\\ a_{\text{ht}} &= \frac{4\pi^2 r}{T^2},\\ \frac{T^2}{r^3} &= \frac{4\pi^2}{GM}. \end{align}$$

Vì $M$ là khối lượng Mặt Trời nên với mọi hành tinh, vế trái của đẳng thức cuối là như nhau. Việc xét chuyển động của hệ hấp dẫn quanh tâm khối cho phép Newton hiệu chỉnh. Dạng tổng quát cho quỹ đạo elip là

$$\frac{T^2}{a^3}\,(m_1+m_2)=\frac{4\pi^2}{G}.$$

Tỉ số giữa bình phương chu kỳ quỹ đạo của hai vật và lập phương khoảng cách trung bình giữa chúng, nhân với tổng khối lượng hai vật, là một hằng số. Hệ thức này cho phép xác định tổng khối lượng của các vật quay quanh nhau, ví dụ các sao đôi hoặc hành tinh có vệ tinh.

5. Phương trình quỹ đạo thiết diện cônic (elip/hypebol) và các tham số $a,e,p,b$

Tùy theo năng lượng toàn phần, vật chuyển động trong trường lực trung tâm theo quỹ đạo elip, parabol hoặc hypebol. Các quỹ đạo như vậy (gọi là các đường cong bậc hai) được mô tả bởi phương trình của các thiết diện cônic. Ta viết phương trình elip trong toạ độ cực với cực tại tiêu điểm của đường cong:

$$r(\varphi)=\frac{p}{1+e\cos\varphi}.$$

Ở đây $p$ là tham số, $e$ là độ lệch tâm (eccentricity) của elip, $\varphi$ là dị thường thật, tức góc tại tiêu điểm giữa hướng đến cận điểm (cận tâm) và hướng đến vị trí của chất điểm.

Làm rõ ý nghĩa của tham số: với $\varphi=\dfrac{\pi}{2}$ thì $r=p$. Nếu $\varphi=0$ thì $p=r_p(1+e)$, còn nếu $\varphi=\pi$ thì $p=r_a(1-e)$. Vì thế

$$r_p+r_a=2a,\qquad p=a(1-e^2),$$

và phương trình elip có dạng

$$r(\varphi)=a\,\frac{1-e^2}{1+e\cos\varphi}.$$

Hình 1

Vì khoảng cách từ tâm elip đến tiêu điểm (xem Hình 1) là $OF=ea$, nên bán trục nhỏ $b=a\sqrt{1-e^2}$. Diện tích elip $S=\pi ab$, hay $S=\pi a^2\sqrt{1-e^2}$. Từ diện tích và chu kỳ có thể biểu diễn tốc độ quét diện tích.

Một số tính chất và đặc trưng của quỹ đạo hypebol sẽ được xét khi phân tích các bài toán cụ thể.

II. Hệ thống các bài toán về chuyển động của các thiên thể trong trường hấp dẫn

Bài toán 1. Chuyển động của dòng các hạt bụi trong trường hấp dẫn của Trái Đất

Dòng các hạt bụi vũ trụ có nồng độ $n$ và khối lượng trung bình $m_0$ chuyển động về phía Trái Đất, với vận tốc tương đối $v_0$ ở khoảng cách rất lớn so với Trái Đất. Trong thời gian $t$, khối lượng bụi vũ trụ nào rơi xuống Trái Đất?

Nếu biết tham số ngắm $r_0$ ứng với trường hợp bắt giữ hấp dẫn các hạt, thì khối lượng vật chất bị bắt giữ được xác định bởi thể tích một hình trụ có bán kính đáy $r_0$ và mật độ bụi $\rho=m_0n$:

$$\Delta m=m_0n\,\pi r_0^2 v_0 t.$$

Tham số ngắm $r_0$ được xác định bởi khoảng cách lớn nhất của các hạt đến trục dòng, sao cho lực hút của trường hấp dẫn còn đủ để…thì hạt sẽ chạm bề mặt Trái Đất tại điểm cận tâm, nơi $r_1=R_\oplus$ (ở đây $\vec{R}_\oplus \perp \vec{v}_1$). Viết tích phân diện tích và định luật bảo toàn năng lượng cho hai trạng thái:

$$\begin{align} r_0v_0 &= R_\oplus v_1,\\ \frac{m_0v_0^2}{2} &= \frac{m_0v_1^2}{2}-\frac{GMm_0}{R_\oplus}. \end{align}$$

Lưu ý rằng $\dfrac{GM}{R_\oplus^2}=g_0$. Do đó $v_1^2=v_0^2+2g_0R_\oplus$ và tham số ngắm

$$r_0=R_\oplus\sqrt{1+\frac{2g_0R_\oplus}{v_0^2}},$$

suy ra khối lượng vật chất rơi xuống Trái Đất:

$$\Delta m=m_0n\,\pi R_\oplus^2\left(1+\frac{2g_0R_\oplus}{v_0^2}\right)v_0t.$$

Bài toán 2. Vệ tinh bị hãm tốc: thời gian rơi từ quỹ đạo tròn sang quỹ đạo elip chạm hành tinh

Một vệ tinh đang chuyển động trên quỹ đạo tròn bán kính $R_c$ bị hãm tốc và chuyển sang quỹ đạo elip, tiếp xúc bề mặt hành tinh bán kính $R_p$ tại cận điểm. Hãy xác định thời gian vệ tinh rơi xuống hành tinh. Khối lượng hành tinh là $M$.

Quỹ đạo mới của vệ tinh là một elip có bán trục lớn $a=\dfrac{R_c+R_p}{2}$, và thời gian rơi bằng nửa chu kỳ, tức $\tau=\dfrac{T}{2}$. Chu kỳ chuyển động trên elip thỏa

$$T^2=\frac{4\pi^2}{GM}\,a^3.$$

Suy ra thời gian rơi theo bán trục lớn của quỹ đạo:

$$\tau=\frac{\pi}{2}\,(R_c+R_p)\sqrt{\frac{R_c+R_p}{2GM}}.$$

Bài toán 3. Tách mô-đun khỏi vệ tinh Mặt Trăng: vận tốc tương đối để rơi theo quỹ đạo bán elip

Vệ tinh Mặt Trăng chuyển động trên quỹ đạo tròn bán kính $R=3{,}4\cdot10^6\,\text{m}$. Từ vệ tinh tách ra một mô-đun, mô-đun này rơi xuống bề mặt Mặt Trăng theo quỹ đạo bán elip. Hỏi tại thời điểm tách ra, mô-đun phải có vận tốc tương đối so với vệ tinh bằng bao nhiêu? Bán kính Mặt Trăng $R_{\text{L}}=1{,}7\cdot10^6\,\text{m}$, và gia tốc rơi tự do trên bề mặt Mặt Trăng nhỏ hơn 6 lần so với trên bề mặt Trái Đất.

Mô-đun xuất phát từ viễn điểm của quỹ đạo elip, với bán trục lớn $$a=\frac{1}{2}(R+R_{\text{L}})=\frac{3}{2}R_{\text{L}}.$$

Vận tốc (độ lớn) tại viễn điểm tìm từ tích phân năng lượng:

$$v_1=\sqrt{\frac{GM}{R}}\;\sqrt{2-\frac{R}{a}},$$

còn vận tốc tròn của vệ tinh:

$$v_c=\sqrt{\frac{GM}{R}}.$$

Vận tốc tương đối (độ lớn) được xác định bởi hiệu các vận tốc:

$$v_{\text{tđ}}=v_c\left(1-\sqrt{2-\frac{R}{a}}\right).$$

Vì gia tốc rơi tự do trên bề mặt Mặt Trăng $g_0=\dfrac{GM}{R_{\text{L}}^2}$, nên

$$\begin{align} v_c &= \sqrt{\frac{GM}{R}}=\sqrt{\frac{g_0}{R}}\,R_{\text{L}},\\ v_{\text{tđ}} &= \sqrt{\frac{g_0}{R}}\,R_{\text{L}}\left(1-\sqrt{2-\frac{4}{3}}\right) =212\,\text{m/s}, \end{align}$$

và hướng của $\vec{v}_{\text{tđ}}$ ngược chiều với vận tốc quỹ đạo.

Bài toán 4. Năng lượng tối thiểu để tàu thăm dò thoát khỏi trường hấp dẫn hành tinh (từ quỹ đạo elip)

Một tàu thăm dò vũ trụ khối lượng $m$ chuyển động quanh hành tinh khối lượng $M$ theo quỹ đạo có khoảng cách lớn nhất đến tâm hành tinh là $r_a$ và nhỏ nhất là $r_p$. Cần truyền cho tàu thăm dò năng lượng tối thiểu bao nhiêu để nó rời khỏi hành tinh?

Trường hấp dẫn là trường thế. Năng lượng cơ học toàn phần của vật khi chuyển động là hằng số và âm đối với quỹ đạo elip. Để thoát khỏi trường hấp dẫn của hành tinh, cần làm cho năng lượng cơ học toàn phần trở thành không âm. Tích phân năng lượng cho quỹ đạo ban đầu có dạng

$$v_r^2=GM\left(\frac{2}{r}-\frac{1}{a}\right),\qquad a=\frac{r_a+r_p}{2}.$$

Từ đó suy ra

$$\frac{mv_r^2}{2}-\frac{GMm}{r}=-\frac{GMm}{2a}.$$

Đây là biểu thức cho năng lượng toàn phần của vệ tinh. Độ tăng tối thiểu cần thiết của chỉ cần tăng năng lượng cơ học toàn phần của vệ tinh lên bằng không, tức là

$$\Delta E_{\min}-\frac{GMm}{2a}=0,$$

từ đó

$$\Delta E_{\min}=\frac{GMm}{2a},\qquad \Delta E_{\min}=\frac{GMm}{r_a+r_p}.$$

Bài toán 5. Chuyển quỹ đạo Trái Đất → Sao Thổ (Hohmann): tính $\Delta v_1$, $\Delta v_2$, thời gian bay và góc phóng

Cần chuyển một tàu vũ trụ từ quỹ đạo gần Trái Đất sang quỹ đạo tròn gần với quỹ đạo của Sao Thổ, theo quỹ đạo bán elip. Việc này đạt được nhờ một lần đổi vận tốc ban đầu $\Delta v_1$ gần quỹ đạo Trái Đất, rồi một lần đổi vận tốc thứ hai $\Delta v_2$ gần quỹ đạo Sao Thổ. Các lần đổi này là do thay đổi xung lượng tức thời, bỏ qua sự thay đổi khối lượng của tàu. Hãy xác định:
1) Vận tốc chuyển động của Trái Đất và Sao Thổ trên các quỹ đạo tròn bán kính tương ứng $r_3=150\cdot10^6\,\text{km}$ và $r_C=1350\cdot10^6\,\text{km}$. Khối lượng Mặt Trời $M=2\cdot10^{30}\,\text{kg}$.
2) Độ biến thiên vận tốc $\Delta v_1$ để chuyển từ quỹ đạo tròn của Trái Đất sang quỹ đạo bán elip.
3) Độ biến thiên vận tốc $\Delta v_2$ cần thiết để chuyển từ quỹ đạo elip sang quỹ đạo tròn của Sao Thổ.
4) Khoảng cách góc giữa Trái Đất và Sao Thổ tại thời điểm phóng, với điều kiện tàu tiếp cận Sao Thổ tại điểm viễn nhật của quỹ đạo.

Vận tốc nhật tâm của Trái Đất và Sao Thổ:

$$\begin{align} v_{r_3} &= \sqrt{\frac{GM}{r_3}}=29{,}78\cdot10^3\,\text{m/s},\\ v_{r_C} &= \sqrt{\frac{GM}{r_C}}=9{,}93\cdot10^3\,\text{m/s}. \end{align}$$

Bán trục lớn của quỹ đạo chuyển tiếp:

$$a=\frac{r_C+r_3}{2}=7{,}5\cdot10^8\,\text{km}.$$

Vận tốc nhật tâm của tàu tại cận nhật (trên quỹ đạo elip) sau khi ra khỏi vùng ảnh hưởng hấp dẫn của Trái Đất (từ tích phân năng lượng):

$$\begin{align} v_{r_1} &= \sqrt{GM\!\left(\frac{2}{r_3}-\frac{1}{a}\right)} = \sqrt{\frac{GM}{r_3}}\;\sqrt{2-\frac{r_3}{a}} = 1{,}342\,v_{r_3}. \end{align}$$

Do đó độ tăng vận tốc thứ nhất nhỏ hơn:

$$\Delta v_1=v_{r_3}(1{,}342-1)=10{,}18\,\text{km/s}.$$

Tương tự, vận tốc tại viễn nhật ($r_2=r_C$):

$$\begin{align} v_{r_2} &= \sqrt{\frac{GM}{r_2}}\;\sqrt{2-\frac{r_C}{a}} = \sqrt{2-\frac{13{,}5}{7{,}5}}\;\cdot 9{,}93\,\text{km/s} = 4{,}44\,\text{km/s}. \end{align}$$

Độ tăng vận tốc để đưa tàu vào quỹ đạo tròn gần Sao Thổ:

$$\Delta v_2=v_{r_C}-v_{r_2}=5{,}49\cdot10^3\,\text{m/s}.$$

Thời gian bay $\tau$ theo quỹ đạo bán elip bằng nửa chu kỳ. Theo định luật Kepler,

$$\left(\frac{T_a}{T_3}\right)^2=\left(\frac{a}{r_3}\right)^3,\qquad \tau=\frac{T_a}{2}=\frac{T_3}{2}\sqrt{\left(\frac{a}{r_3}\right)^3}\approx 5{,}59\,\text{năm}.$$

Gọi $\varphi_{3C}$ là góc giữa Trái Đất và Sao Thổ tại thời điểm xuất phát, còn $\Delta\varphi_C$ là góc quay của bán kính vectơ Sao Thổ quanh Mặt Trời trong thời gian bay. Vì quỹ đạo chuyển tiếp là bán elip nên góc quét tương ứng bằng $\pi$. Do đó

$$\varphi_{3C}+\Delta\varphi_C=\pi,\qquad \frac{2\pi}{T_C}=\frac{\Delta\varphi_C}{\tau},\qquad \Delta\varphi_C=2\pi\frac{\tau}{T_C},$$

trong đó $T_C=29{,}46\,\text{năm}$ là chu kỳ quỹ đạo của Sao Thổ. Suy ra

$$\varphi_{3C}=\pi\left(1-\frac{2\tau}{T_C}\right) =\pi\left(1-\frac{11{,}18}{29{,}46}\right) =0{,}62\pi \approx 111{,}7^\circ.$$

Bài toán 6. Phóng tàu vào quỹ đạo quanh Mặt Trời có cận nhật $0.01$ AU: góc bẻ vận tốc và vận tốc phóng

Cần đưa một tàu vũ trụ lên quỹ đạo quanh Mặt Trời có cận nhật bằng $0{,}01$ bán kính quỹ đạo Trái Đất, và chu kỳ bằng chu kỳ Trái Đất quay quanh Mặt Trời. Cần phóng tàu từ Trái Đất với vận tốc bao nhiêu và theo hướng nào so với bán kính vectơ Mặt Trời–Trái Đất? Vận tốc quỹ đạo của Trái Đất $v_1=30\,\text{km/s}$.

Bán trục lớn của quỹ đạo tàu phải bằng bán kính quỹ đạo Trái Đất, vì chu kỳ của nó phải bằng chu kỳ Trái Đất (hệ quả của định luật Kepler thứ ba). Khi đó từ tích phân năng lượng suy ra vận tốc nhật tâm của tàu phải bằng vận tốc quỹ đạo của Trái Đất. Có thể đạt quỹ đạo elip yêu cầu bằng cách đổi hướng của vận tốc khi tàu đi ra khỏi vùng ảnh hưởng hấp dẫn của Trái Đất so với vectơ bán kính Mặt Trời – Trái Đất. Để ước lượng góc cần thiết khi đi ra quỹ đạo nhật tâm, ta đặt bằng mômen động lượng của tàu tại điểm “thoát” và tại cận nhật; đồng thời biểu diễn vận tốc ở cận nhật từ tích phân năng lượng:

$$\begin{align} rmv_1\sin\alpha &= r_pmv_p\sin90^\circ = r_pmv_p. \end{align}$$

$$\begin{align} v_p &= \sqrt{\frac{GM}{r}\left(\frac{2}{0.01}-1\right)} = v_1\sqrt{199},\\ \sin\alpha &= \frac{r_pv_p}{rv_1}=0.14,\qquad \alpha=8^\circ. \end{align}$$

Đây là góc giữa các hướng $\vec r_1$ và $\vec v_1$, tức là cần “bẻ” vectơ vận tốc quỹ đạo một góc $\varphi=90^\circ-\alpha=82^\circ$.

Vận tốc bổ sung được xác định từ tam giác vận tốc:

$$\begin{align} v_{\text{bổ sung}} &=2v_1\sin\frac{\varphi}{2} =60\,\text{km/s}\cdot\sin41^\circ\\ &=60\,\text{km/s}\cdot0.656 =39.4\,\text{km/s}. \end{align}$$

Tổng vectơ của vận tốc bổ sung với vận tốc quỹ đạo của Trái Đất cho vận tốc nhật tâm ở “đầu ra” sau khi vượt qua trường hấp dẫn của Trái Đất. Vì vậy năng lượng toàn phần lúc phóng phải tính cả thế năng hấp dẫn của Trái Đất:

$$\begin{align} \frac{mv_{\text{phóng}}^{2}}{2}-\frac{GM_\oplus m}{R_\oplus} &= \frac{mv_{\text{bổ sung}}^{2}}{2},\\ \frac{2GM_\oplus}{R_\oplus} &= v_{\text{thoát}}^{2},\\ v_{\text{phóng}}^{2} &= v_{\text{thoát}}^{2}+v_{\text{bổ sung}}^{2},\\ v_{\text{phóng}} &= \sqrt{11.2^{2}+39.4^{2}}\;\text{km/s}=41\;\text{km/s}. \end{align}$$

Bài toán 7. Quỹ đạo hypebol bay sượt hành tinh: khoảng cách tiếp cận tối thiểu và góc lệch quỹ đạo

Khi đi vào “vùng ảnh hưởng” của một hành tinh khối lượng $M$, một vật thể vũ trụ có vận tốc tương đối so với hành tinh là $v_0$ và tham số ngắm (khoảng cách va chạm) $b$. Vật thể sẽ đi qua hành tinh ở khoảng cách tối thiểu nào và vận tốc của nó bị đổi hướng một góc bao nhiêu do trường hấp dẫn của hành tinh?

Với điều kiện đã cho, quỹ đạo của vật đối với hành tinh là một hypebol, trong đó tâm hút nằm ở một tiêu điểm. Hướng vận tốc lúc đi vào và lúc đi ra trùng với các tiệm cận của hypebol; góc đổi hướng của vận tốc là góc giữa hai tiệm cận, ký hiệu $\varphi$. Tại đỉnh $A$, vận tốc vuông góc với hướng đến tiêu điểm $F$. Xét hai trạng thái: (1) lúc vật đi vào vùng ảnh hưởng, và (2) lúc vật ở đỉnh $A$; ta viết bảo toàn năng lượng và mômen động lượng:

$$\begin{align} \frac{mv_0^{2}}{2} &= \frac{mv_1^{2}}{2}-\frac{GMm}{r_1},\\ mv_0b &= mv_1r_1. \end{align}$$

Suy ra

$$\begin{align} v_1 &= \frac{b}{r_1}\,v_0,\\ \frac{2GM}{r_1} &= \frac{b^{2}-r_1^{2}}{r_1^{2}}\,v_0^{2}, \qquad \text{hay}\qquad \frac{2GM}{v_0^{2}}=\frac{b^{2}-r_1^{2}}{r_1}\;(*). \end{align}$$

$$r_1=-\frac{GM}{v_0^{2}}+\sqrt{\left(\frac{GM}{v_0^{2}}\right)^{2}+b^{2}}.$$

Ta thu được biểu thức xác định khoảng cách tiếp cận tối thiểu $r_1$ theo $v_0$ và $b$. Để tìm góc đổi hướng $\varphi$, xét hình học hypebol (xem Hình 1). Khoảng cách giữa hai tiêu điểm:

$$FF' = 2(r_1+a)=\frac{2b}{\cos(\varphi/2)}.$$

Theo tính chất cơ bản của hypebol, hiệu khoảng cách từ một điểm bất kỳ đến hai tiêu điểm là không đổi. Áp dụng cho đỉnh hypebol $A$ và cho một điểm rất xa trên quỹ đạo (khi các hướng đến hai tiêu điểm gần như song song), ta có:

$$\Delta r = 2a_1=\frac{2b}{\cos(\varphi/2)}-2r_1,\qquad \Delta r = 2a = 2b\,\tan\frac{\varphi}{2}.$$

Từ tam giác vuông $DFO$:

$$\tan\frac{\varphi}{2}=\frac{a}{b},\qquad \cos\frac{\varphi}{2}=\frac{b}{r_1+a},$$

suy ra

$$\frac{b^{2}-r_1^{2}}{2r_1}=a,\qquad \tan\frac{\varphi}{2}=\frac{b^{2}-r_1^{2}}{2br_1}.$$

Kết hợp với biểu thức $(*)$ ta được:

$$\varphi = 2\arctan\!\left(\frac{GM}{bv_0^{2}}\right).$$

Vật rời khỏi vùng ảnh hưởng của hành tinh với độ lớn vận tốc tương đối bằng đúng khi đi vào. Nhưng vận tốc nhật tâm vận tốc, tức là tổng vectơ của vận tốc tương đối của vật đối với hành tinh và vận tốc của chính hành tinh, có thể thay đổi đáng kể, kéo theo quỹ đạo cũng thay đổi. Nếu bảo đảm cho tàu vũ trụ bay sượt gần hành tinh, ta có thể thay đổi vận tốc nhật tâm và quỹ đạo của nó nhờ trường hấp dẫn của hành tinh.

Bài toán 8. Vượt vận tốc vũ trụ cấp ba: vận tốc thoát theo hệ nhật tâm và góc tiệm cận quỹ đạo hypebol

Một tàu vũ trụ xuất phát từ Trái Đất với vận tốc $v_0$ lớn hơn vận tốc vũ trụ cấp ba, theo hướng chuyển động quỹ đạo của Trái Đất (tức vuông góc với hướng về phía Mặt Trời). Khi ra khỏi “vùng ảnh hưởng” của Trái Đất, quỹ đạo của tàu trong hệ nhật tâm là một hypebol (Hình 2), có đỉnh $E$ (Trái Đất) và tiêu điểm $S$ (Mặt Trời). Hãy xác định độ lớn vận tốc $v_k$ của tàu so với Mặt Trời ở rất xa Mặt Trời. Vận tốc đó hợp với hướng $ES$ một góc $\alpha$ bằng bao nhiêu?

Hình 2

Khi rời khỏi vùng ảnh hưởng của Trái Đất, tàu có vận tốc tương đối so với Trái Đất là $v$. Theo định luật bảo toàn năng lượng (trong trường hấp dẫn của Trái Đất),

$$\frac{mv_0^2}{2}-\frac{GM_\oplus m}{R_\oplus}=\frac{mv^2}{2}.$$

Mà $\dfrac{2GM_\oplus}{R_\oplus}=v_{\text{thoát}}^2$, trong đó $v_{\text{thoát}}=11.2\,\text{km/s}$ là vận tốc thoát (vận tốc “parabol”) của Trái Đất. Do đó

$$v=\sqrt{v_0^2-v_{\text{thoát}}^2}.$$

Theo giả thiết, vận tốc bổ sung $v$ cùng hướng với vận tốc quỹ đạo của Trái Đất, nên vận tốc nhật tâm của tàu tại “đỉnh hypebol” là

$$v_r=v+v_{\text{orb}},$$

trong đó $v_{\text{orb}}=29.8\,\text{km/s}$ là vận tốc quỹ đạo của Trái Đất quanh Mặt Trời. Khi bay ra xa trong trường hấp dẫn của Mặt Trời, vận tốc nhật tâm giảm xuống còn $v_k$. Theo bảo toàn năng lượng trong trường hấp dẫn của Mặt Trời,

$$\frac{mv_r^2}{2}-\frac{GM_\odot m}{r_{\oplus 0}}=\frac{mv_k^2}{2}.$$

Với $\dfrac{GM_\odot}{r_{\oplus 0}}=v_{\text{orb}}^2$, ta được

$$v_r^2-2v_{\text{orb}}^2=v_k^2,$$

hay cuối cùng

$$v_k=\sqrt{\left(\sqrt{v_0^2-v_{\text{thoát}}^2}+v_{\text{orb}}\right)^2-2v_{\text{orb}}^2}.$$

Tàu chuyển động trong trường hấp dẫn của Mặt Trời theo một nhánh hypebol; khi đó mômen động lượng được bảo toàn. Gọi $b$ là tham số ngắm (impact parameter) của tàu đã “thoát”, ta có

$$mv_r\,r_{\oplus 0}=mv_k\,b,\qquad b=\frac{v_r}{v_k}\,r_{\oplus 0}.$$

Từ Hình 2: $ES=r_{\oplus 0}$ là bán kính quỹ đạo Trái Đất, $OE=a$ là khoảng cách từ tâm hypebol đến đỉnh. Góc cần tìm $\alpha$ là góc mà tiệm cận hypebol tạo với hướng $ES$. Theo tính chất cơ bản của hypebol, hiệu khoảng cách từ mọi điểm đến hai tiêu điểm $S$ và $S_1$ là không đổi. Áp dụng cho đỉnh $E$ và cho một điểm rất xa $M$ (khi các hướng đến hai tiêu điểm gần như song song), ta thu được:

$$r_1-r_2=2a,\qquad r_1-r_2=\frac{2b}{\tan\alpha},$$

suy ra

$$\tan\alpha=\frac{b}{a}.$$

Biểu diễn $a$ từ tam giác vuông có hai cạnh góc vuông $a$ và $b$, cạnh huyền $a+r$ (với $r=r_{\oplus 0}$):

$$\begin{align} a^2+b^2 &= a^2+2ar+r^2,\\ a &= \frac{b^2-r^2}{2r}. \end{align}$$

Thế vào (với $b=\dfrac{v_r}{v_k}r$) ta được

$$\tan\alpha=\frac{2\,\dfrac{v_r}{v_k}}{\left(\dfrac{v_r}{v_k}\right)^2-1}, \qquad \alpha=\arctan\!\left(\frac{2\,\dfrac{v_r}{v_k}}{\left(\dfrac{v_r}{v_k}\right)^2-1}\right).$$

Bài toán 9. Vượt vận tốc vũ trụ cấp ba: vận tốc thoát theo hệ nhật tâm và góc tiệm cận quỹ đạo hypebol

Một tàu vũ trụ, khi thực hiện “cú hích hấp dẫn” (gravity assist) trong vùng lân cận Sao Hỏa, đi vào một quỹ đạo nhật tâm mới; trên quỹ đạo này nó gặp một tiểu hành tinh tại điểm viễn nhật. Điểm chuyển sang quỹ đạo mới ứng với tham số tiêu (tham số quỹ đạo) của elip; tại đó tàu chuyển động theo hướng bán trục nhỏ của quỹ đạo. Chu kỳ chuyển động trên quỹ đạo mới là 10 năm. Ở điểm chuyển quỹ đạo, các tấm pin Mặt Trời được bung ra với diện tích $30\,\text{m}^2$ và hiệu suất $25\%$. Hãy ước lượng năng lượng Mặt Trời mà tàu thu được trong thời gian bay. Độ lệch tâm của quỹ đạo mới bằng bao nhiêu?

Dùng phương trình elip trong tọa độ cực:

$$r(\varphi)=\frac{p}{1+e\cos\varphi},$$

trong đó $p$ là tham số tiêu (tham số quỹ đạo), $e$ là độ lệch tâm, $\varphi$ là góc giữa vectơ bán kính $r$ và hướng từ tiêu điểm đến cận nhật (dị thường thật). Từ phương trình suy ra: tại điểm chuyển quỹ đạo $r_0=p$ khi $\cos\varphi_0=0$, tức $\varphi_0=\dfrac{\pi}{2}$; còn tại viễn nhật thì $\varphi_k=\pi$.

Chu kỳ xác định bán trục lớn $a$ theo định luật Kepler thứ ba. Nếu $a$ tính bằng AU và $T$ tính bằng năm, thì

$$\begin{align} a &= T^{2/3} = 4.64\,\text{AU}. \end{align}$$

Tham số $p$ liên hệ với $a$ bởi $p=a(1-e^2)$, và trong bài toán này $p$ đúng bằng khoảng cách nhật tâm của Sao Hỏa, tức $p=1.52\,\text{AU}$. Do đó

$$\begin{align} p &= a(1-e^2)=1.52\,\text{AU},\\ e &= \sqrt{1-\frac{p}{a}}=0.82. \end{align}$$

Bán trục nhỏ:

$$b=a\sqrt{1-e^2}=2.66\,\text{AU}.$$

Tấm pin hướng về phía Mặt Trời. Với độ trưng (công suất bức xạ) của Mặt Trời $L=3.86\cdot10^{26}\,\text{W}$, trong một khoảng thời gian rất nhỏ $dt$ tại khoảng cách $r$, năng lượng thu được là

$$dW=\eta S\,\frac{L}{4\pi r^2}\,dt,\qquad (1)$$

trong đó $\eta$ là hiệu suất, $S$ là diện tích tấm pin. Tốc độ quét diện tích của vectơ bán kính là hằng số (định luật Kepler 2):

$$\begin{align} \dot{\vec s} &= [\vec r\times\vec v],\\ |\dot{\vec s}| &= r\,v_n = r^2\omega, \end{align}$$

với $\omega=\dfrac{d\varphi}{dt}$ là tốc độ góc của vectơ bán kính. Biểu diễn tốc độ quét diện tích qua chu kỳ, ta được

$$\begin{align} \omega &= \frac{2\pi ab}{T}\cdot\frac{1}{r^2} = \frac{d\varphi}{dt}, \end{align}$$

suy ra

$$dt=\frac{Tr^2}{2\pi ab}\,d\varphi. \qquad (2)$$

Thế (2) vào (1) ta nhận được quan hệ giữa các vi phân:

$$dW=\eta S\,\frac{L}{4\pi r^2}\cdot\frac{Tr^2}{2\pi ab}\,d\varphi.$$

Chuyển sang năng lượng toàn phần trên đoạn bay. Vì $\varphi_{\text{tổng}}=\pi-\dfrac{\pi}{2}=\dfrac{\pi}{2}$, nên năng lượng thu được trên đoạn quỹ đạo này là

$$W_{\text{tổng}}=\eta S\,\frac{LT}{16\pi ab}.$$

Lấy $1\,\text{AU}=1.5\cdot10^{11}\,\text{m}$ và $T=31.56\cdot10^{7}\,\text{s}$. Khi đổi $a$ sang mét và $T$ sang giây, ta ước lượng được:

$$W_{\text{tổng}}\approx 2\cdot10^{9}\,\text{J}.$$

III. Các bài tập tự giải về chuyển động của các thiên thể trong trường hấp dẫn

1. Từ chu kỳ quay của Trái Đất và bán kính quỹ đạo Trái Đất, hãy ước lượng khối lượng Mặt Trời. Mật độ trung bình của vật chất Mặt Trời bằng bao nhiêu nếu đường kính góc của đĩa Mặt Trời quan sát từ Trái Đất là $32$ phút cung?
2. Hai ngôi sao có khối lượng xấp xỉ như nhau $m$ quay quanh tâm khối chung. Khoảng cách giữa hai sao là $R$. Chu kỳ quay của hệ bằng bao nhiêu?
3. Một tàu vũ trụ xuất phát từ bề mặt Trái Đất. Vận tốc tối thiểu ngay sau khi phóng cần có để đạt tới quỹ đạo Sao Hỏa (bán kính $r=1.52\,\text{AU}$) là bao nhiêu, nếu bỏ qua ảnh hưởng của khí quyển?
4. Sao chổi Halley có cận nhật cách Mặt Trời $0.6\,\text{AU}$. Chu kỳ của nó là $76$ năm. Ở viễn nhật, sao chổi sẽ cách Mặt Trời bao nhiêu?

---

Lời kết

Nếu coi mỗi bài toán trong bài là một “mảnh ghép”, thì hai nguyên lý bảo toàn (mômen động lượng và năng lượng) chính là “chìa khoá chung” để mở hầu hết các bài toán quỹ đạo trong trường hấp dẫn. Bạn có thể dùng bài này như một trang tổng hợp công thức khi ra đề, chữa đề hoặc luyện đội tuyển HSG/Olympic.

Bạn muốn mình soạn thêm một bộ 20–30 bài tập chọn lọc kèm phân loại mức độ (HSG tỉnh → HSG QG → Olympic) không? Nếu có, bạn cho mình biết mức bạn muốn và dạng đề bạn hay gặp, mình sẽ gợi ý cấu trúc bộ bài cho đúng nhu cầu.

Read More