Câu 1. Rơi một quả cầu trong hồ nước
1) Thời gian từ mặt nước đến đáy hồ (độ sâu $e=5\,\text{m}$)
Bước 1. Vận tốc của quả cầu ngay khi chạm mặt nước
\begin{align} mgh&=\frac12 mv^2\\ v&=\sqrt{2gh}=\sqrt{2\cdot 9.8\cdot 10}=14\,\text{m/s} \end{align} Bước 2. Gia tốc của quả cầu khi chuyển động trong nước (bỏ qua lực cản)
Trong nước: $P=\rho_s gV$, lực đẩy Ác-si-mét $F_A=\rho_l gV$, khối lượng $m=\rho_s V$.
\begin{align} P-F_A&=ma\\ \rho_s gV-\rho_l gV&=\rho_s Va\\ a&=\frac{(\rho_s-\rho_l)g}{\rho_s} \end{align} Thay $\rho_s=7500\,\text{kg/m}^3$, $\rho_l=1000\,\text{kg/m}^3$:
\begin{align} a&=\frac{(7500-1000)\cdot 9.8}{7500}=8.49\,\text{m/s}^2 \end{align} Bước 3. Tính thời gian đi từ mặt nước đến đáy hồ (chọn chiều dương hướng xuống, $v_i=14\,\text{m/s}$)
\begin{align} e&=v_it+\frac{a}{2}t^2\\ 5&=14t+\frac{8.49}{2}t^2\\ 0&=4.245t^2+14t-5 \end{align} Nghiệm dương: $\;t=0.325\,\text{s}$.
2) Động năng, thế năng trên đơn vị khối lượng và xét bảo toàn
Chọn mốc thế năng tại mặt nước
a) Trước khi thả (ở độ cao $+10\,\text{m}$, $v_0=0$)
\begin{align} \frac{T_i}{m}&=\frac12 v_0^2=0\;\text{J/kg}\\ \frac{V_i}{m}&=g\cdot 10=98\;\text{J/kg} \end{align} b) Tại đáy hồ (ở độ sâu $-5\,\text{m}$)
Trước hết cần vận tốc ở đáy hồ:
\begin{align} v_f&=v_i+at\\ &=14+8.49\cdot 0.325\\ &\approx 16.76\,\text{m/s} \end{align} Khi đó:
\begin{align} \frac{T_f}{m}&=\frac12 v_f^2=\frac12\cdot 16.76^2=140.47\;\text{J/kg}\\ \frac{V_f}{m}&=g\cdot(-5)=-49\;\text{J/kg} \end{align} c) So sánh tổng $\frac{T}{m}+\frac{V}{m}$
\begin{align} \frac{E_i}{m}&=\frac{T_i}{m}+\frac{V_i}{m}=98\;\text{J/kg}\\ \frac{E_f}{m}&=\frac{T_f}{m}+\frac{V_f}{m}=140.47-49=91.47\;\text{J/kg} \end{align} Chênh lệch: $\;98-91.47=6.53\,\text{J/kg}$.
Kết luận & giải thích: Tổng $\frac{T}{m}+\frac{V}{m}$ của riêng quả cầu không bảo toàn vì trong nước có lực đẩy Ác-si-mét (lực ngoài đối với hệ “quả cầu”). Nếu xét đầy đủ năng lượng của hệ mở rộng, cần cộng thêm thế năng tăng lên của phần nước bị chiếm chỗ (tương đương khối nước đó được “nâng” lên $5\,\text{m}$):
\begin{align} \frac{V_{\text{nước}}}{m} &=\frac{m_{\text{nước}}}{m}gh =\frac{\rho_l}{\rho_s}gh =\frac{1000}{7500}\cdot 9.8\cdot 5 =6.53\,\text{J/kg} \end{align} Do đó, khi tính thêm phần này thì phù hợp với bảo toàn năng lượng.
3) Độ sâu lớn nhất của quả cầu có khối lượng riêng $0.3\,\text{g/cm}^3$
Với $\rho_s=300\,\text{kg/m}^3$:
\begin{align} a&=\frac{(\rho_s-\rho_l)g}{\rho_s} =\frac{(300-1000)\cdot 9.8}{300} =-22.87\,\text{m/s}^2 \end{align} Quả cầu vào nước với $v_i=14\,\text{m/s}$ (hướng xuống) và chậm dần đến khi $v=0$:
\begin{align} t&=\frac{v_f-v_i}{a}=\frac{0-14}{-22.87}=0.61\,\text{s} \end{align} Độ sâu cực đại:
\begin{align} e_{\max}&=v_it+\frac{a}{2}t^2\\ &=14\cdot 0.61+\frac{-22.87}{2}\cdot 0.61^2\\ &=4.29\,\text{m} \end{align}
4) Thời gian rơi đến mặt nước trên hành tinh mới
Hành tinh có cùng khối lượng như Trái Đất nhưng bán kính bằng một nửa, nên $g\propto \dfrac{1}{R^2}$:
\begin{align} \frac{g_p}{g_T}&=\frac{R_T^2}{(R_T/2)^2}=4\\ g_p&=4g_T=4\cdot 9.8=39.2\,\text{m/s}^2 \end{align} Thả rơi tự do từ nghỉ ở độ cao $h=10\,\text{m}$:
\begin{align} h&=\frac{g_p}{2}t^2\\ t&=\sqrt{\frac{2h}{g_p}}=\sqrt{\frac{20}{39.2}}\approx 0.71\,\text{s} \end{align}
Câu 2. Khảo sát đặc tuyến $V-A$ - Đáp án Đề thi học sinh giỏi Vật lý 12 chương trình GDPT 2018 gắn với các tình huống thực tiễn
1) Gắn nhãn ampe kế và vôn kế
Trong mạch khảo sát đặc tuyến $I-V$ của linh kiện cần đo:
– Ampe kế phải mắc nối tiếp với linh kiện để đo dòng qua linh kiện $\Rightarrow$ dụng cụ hình tròn nằm trên nhánh nối từ con chạy (wiper) sang linh kiện $X$ là A.
– Vôn kế phải mắc song song với linh kiện để đo hiệu điện thế hai đầu linh kiện $\Rightarrow$ dụng cụ hình tròn mắc song song với $X$ (nhánh bên phải) là V.
2) Vị trí N để vôn kế chỉ 0
Vôn kế chỉ $0$ khi hiệu điện thế hai đầu $X$ bằng $0$, tức là điểm nối sang $X$ (điểm lấy điện áp ở con chạy) có cùng thế điện với điểm dưới của $X$ (thanh dây dưới – mass của mạch).
Do đó, cần đặt con chạy ở tận cùng phía dưới của điện trở biến đổi (nút dưới, nối với dây dưới). Ký hiệu vị trí này là N.
Thông tin từ đồ thị (Hình 2)
Đồ thị cho quan hệ $I!-!V$ của hai linh kiện X và Y. Nhận xét nhanh:
– Đường của X là đường thẳng qua gốc $\Rightarrow$ X gần như điện trở thuần (ohmic).
– Đường của Y là đường cong $\Rightarrow$ Y là linh kiện không ohmic.
3) Tìm dòng điện để $R_X = R_Y$ và tính $R$
Tại một điểm làm việc, điện trở tức thời được hiểu theo tỉ số $R=\dfrac{V}{I}$. Khi $R_X = R_Y$ (ở cùng một dòng điện tại điểm làm việc tương ứng), ta cần có:
\begin{align}
R_X=R_Y ;\Longleftrightarrow; \frac{V_X}{I}=\frac{V_Y}{I}
;\Longleftrightarrow; V_X=V_Y
\end{align}
Vì vậy, ta tìm giao điểm của hai đường đặc tuyến trên đồ thị (cùng $V$, cùng $I$). Từ hình, giao điểm xấp xỉ:
\begin{align}
V \approx 10,\text{V},\qquad I \approx 0.40,\text{A}
\end{align}
Suy ra:
\begin{align}
R=\frac{V}{I}\approx \frac{10}{0.40}=25,\Omega
\end{align}
Vậy dòng điện cần tìm khoảng $I\approx 0.40,\text{A}$ và điện trở tương ứng khoảng $R\approx 25,\Omega$.
4) Giải thích dạng đặc tuyến của Y
Đặc tuyến của Y cong xuống: khi $V$ tăng thì $I$ vẫn tăng nhưng tốc độ tăng giảm dần (độ dốc $\Delta I/\Delta V$ giảm), tương đương điện trở $R=V/I$ tăng theo dòng điện.
Một giải thích vật lý hợp lý: Y có thể là bóng đèn sợi đốt (hoặc một phần tử có hệ số nhiệt dương – PTC). Khi dòng điện tăng, linh kiện nóng lên làm điện trở suất tăng, nên điện trở tăng và đặc tuyến trở nên phi tuyến.
Mạch ứng dụng (Hình 3): X và Y song song, nối tiếp với Z, nguồn 12 V
Cho biết hiệu điện thế hai đầu mỗi nhánh $X$ và $Y$ là:
\begin{align}
V_X=V_Y=5,\text{V}
\end{align}
Do $X$ và $Y$ mắc song song, nên dòng tổng đi qua mạch là:
\begin{align}
I_{\text{tổng}}=I_X+I_Y
\end{align}
5) Tính $I_X$, $I_Y$ và $I_{\text{tổng}}$
Từ đồ thị tại $V=5,\text{V}$:
– Với X (đường thẳng qua $(10,\text{V},,0.40,\text{A})$), suy ra $I$ tỉ lệ với $V$:
\begin{align}
I_X(5,\text{V}) \approx 0.20,\text{A}
\end{align}
– Với Y (đọc trên đường cong tại $V=5,\text{V}$), xấp xỉ:
\begin{align}
I_Y(5,\text{V}) \approx 0.31,\text{A}
\end{align}
Vậy:
\begin{align}
I_{\text{tổng}} \approx 0.20+0.31=0.51,\text{A}
\end{align}
6) Tính điện trở $Z$
Nguồn $12,\text{V}$, nhánh song song $X\parallel Y$ có $5,\text{V}$, nên phần còn lại rơi trên $Z$:
\begin{align}
V_Z=12-5=7,\text{V}
\end{align}
Dòng qua $Z$ chính là dòng tổng $I_{\text{tổng}}$:
\begin{align}
R_Z=\frac{V_Z}{I_{\text{tổng}}}\approx \frac{7}{0.51}\approx 13.7,\Omega
\end{align}
7) Điện trở tương đương toàn mạch
Điện trở tương đương nhìn từ nguồn:
\begin{align}
R_{\text{eq}}=\frac{U}{I_{\text{tổng}}}\approx \frac{12}{0.51}\approx 23.5,\Omega
\end{align}
Kết quả gần đúng: $I\approx 0.40,\text{A}$, $R\approx 25,\Omega$; $I_{\text{tổng}}\approx 0.51,\text{A}$; $R_Z\approx 13.7,\Omega$; $R_{\text{eq}}\approx 23.5,\Omega$.
Câu 3. Trao đổi nhiệt qua cửa ra vào
1) Lượng nhiệt mất mát
Một sự thay đổi nhiệt độ $\Delta T$ của một hệ có khối lượng $m$ và nhiệt dung riêng $c$ yêu cầu một sự truyền năng lượng nhiệt $Q$ được cho bởi công thức: $$Q = m c \Delta T$$ Nếu $\rho$ là khối lượng riêng và $V$ là thể tích của hệ, ta có: $$m = \rho V$$ Do đó, trong trường hợp của chúng ta (với $\Delta T = T_{int} - T_{ext}$), năng lượng nhiệt mất đi là: $$Q = \rho V c (T_{int} - T_{ext}) \quad (1)$$
Cửa Thông Thường
2) Xác định Thể tích Không khí lạnh $V$
Quan sát Hình 3, ta dễ dàng suy ra rằng, nếu $S$ là tiết diện mà không khí lạnh đi vào với vận tốc $v$, thể tích không khí $V$ đi qua bề mặt đó trong khoảng thời gian $\tau$ là: $$V = v S \tau$$ Với các dữ liệu đã cho trong đề bài, và biểu thị kết quả chỉ với hai chữ số có nghĩa, vì các dữ liệu có độ chính xác này, ta có: $$V = 11 \, \text{m}^3$$
3) Tính Năng lượng Nhiệt $Q$
Thay thế thể tích trên và các dữ liệu đã cho vào công thức (1), ta được: $$Q = 3.1 \times 10^5 \, \text{J}$$ Vì $1 \, \text{kW} \cdot \text{h} = 1000 \, \text{J}/\text{s} \times 3600 \, \text{s} = 3.6 \times 10^6 \, \text{J}$, hoặc ngược lại, $1 \, \text{J} = 2.78 \times 10^{-7} \, \text{kW} \cdot \text{h}$, nên: $$Q = 8.6 \times 10^{-2} \, \text{kW} \cdot \text{h}$$
Cửa Xoay
4) Tính Thể tích Không khí lạnh $V'$
Quan sát Hình 2, góc mà cửa phải xoay để một người có thể đi vào bên trong là $180^\circ$. Do đó, thể tích $V'$ không khí lạnh đã đi vào là thể tích của nửa hình trụ có bán kính $r$ và chiều cao $h$: $$V' = \frac{1}{2} \pi r^2 h$$ Kết quả là: $$V' = 3.6 \, \text{m}^3$$
5) Tính Năng lượng Nhiệt $Q'$
Với thể tích $V'$ này và sử dụng lại công thức (1), ta thu được: $$Q' = 1.0 \times 10^5 \, \text{J}$$ Hoặc: $$Q' = 2.9 \times 10^{-2} \, \text{kW} \cdot \text{h}$$Lưu ý rằng, với mô hình được xem xét, tổn thất nhiệt do sự đi vào của một người qua cửa xoay nhỏ hơn đáng kể so với cửa thông thường.
Câu 4. Giải bài toán – Con lắc đơn dao động điều hòa
1) Tính tần số dao động
Từ đồ thị: tại t = 0.3 s thì \( v = 0.5v_{max} \Rightarrow \cos(\omega \cdot 0.3) = 0.5 \).
Suy ra: \( \omega = \dfrac{10\pi}{9}\,\text{rad/s} \), \( T = 1.8\,\text{s} \), \( f \approx 0.56\,\text{Hz} \).
2) Lập phương trình dao động
Quãng đường vật đi từ $t = 0.3\ \text{s}$ đến $t = 0.6\ \text{s}$ là: $$S = 2\left(A - A\dfrac{\sqrt{3}}{2}\right) = 2.28\,\text{cm}$$ Giải được biên độ: $$A \approx 8.5\,\text{cm}$$ Từ đồ thị ta thấy kh $t=0$ thì $v=v_\text{max}$, tức là pha ban đầu bằng $-\frac{\pi}{2}$ Phương trình dao động: $$x = 8.5\cos\left(\dfrac{10\pi}{9}t-\frac{\pi}{2}\right)\ \text{(cm)}$$
Câu 5. Đo bước sóng laser - Đề thi học sinh giỏi Vật lý 12 chương trình GDPT 2018 gắn với các tình huống thực tiễn
1) Việc hoàn thành bảng dữ liệu mang lại kết quả như sau::
| $m$ | $y_m\ \text{(cm)}$ |
|---|---|
| 0 | 0.0 |
| 1 | 1.5 |
| 2 | 3.0 |
| 3 | 4.7 |
| 4 | 6.2 |
| 5 | 7.8 |
| 6 | 9.3 |
2) Dữ liệu trên có thể được biểu diễn để thu được hình sau.
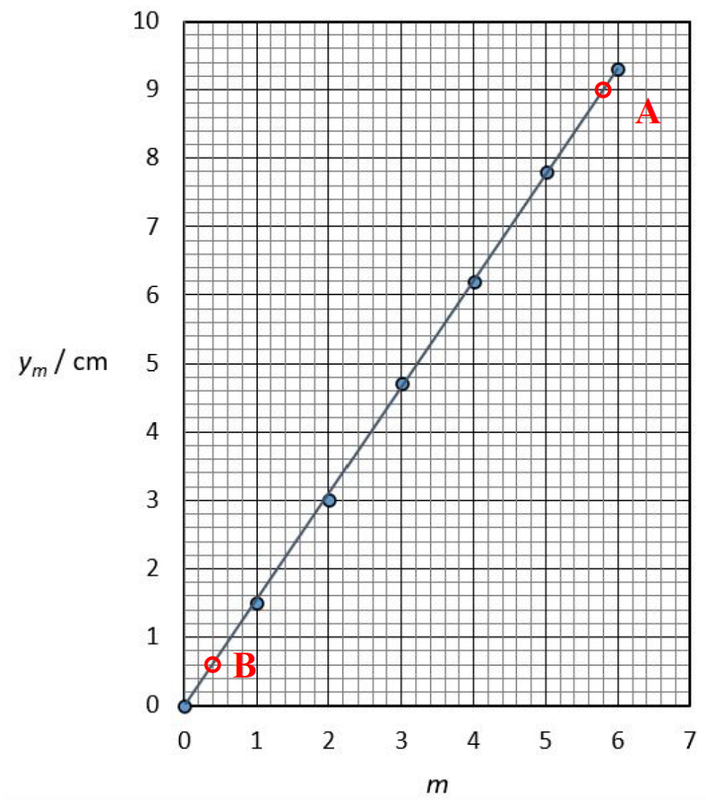
3) Từ đồ thị, suy ra hệ số góc (độ dốc) của đường thẳng là: \begin{align} k&=\frac{y_{m,A}-y_{m,B}}{m_A-m_B}\\ &=\frac{9.0\,\text{cm}-0.6\,\text{cm}}{5.8-0.4}\\ &=1.56\,\text{cm}\\ &=1.56\times 10^{-2}\,\text{m}. \end{align} 4) Nhắc lại rằng $d=0.052\,\text{mm}=5.2\times 10^{-5}\,\text{m}$ và $x=1.55\,\text{m}$, từ hệ thức $$k=\frac{\lambda x}{d}$$ ta suy ra \begin{align} \lambda&=k\frac{d}{x}\\ &=1.56\times 10^{-2}\cdot \frac{5.2\times 10^{-5}}{1.55}\\ &\approx 5.2\times 10^{-7}\,\text{m}\\ &=520\,\text{nm}. \end{align} Giá trị này phù hợp với màu xanh lục của laser được dùng. Giá trị danh định của bước sóng laser là $5.32\times 10^{-7}\,\text{m}=532\,\text{nm}.$



0 nhận xét:
Đăng nhận xét