Đáp án đề thi học sinh giỏi Vật lí 12 tỉnh Quảng Trị 2025 - 2026 được biên soạn nhằm hỗ trợ học sinh và giáo viên trong việc tham khảo, đối chiếu kết quả làm bài sau kì thi. Nội dung bài viết trình bày lời giải chi tiết, bám sát cấu trúc đề chính thức, giúp người đọc hiểu rõ phương pháp tư duy và cách xử lí từng dạng bài thường gặp trong các kì thi học sinh giỏi cấp tỉnh. Đây là tài liệu hữu ích cho quá trình ôn luyện Vật lí 12 nâng cao cũng như chuẩn bị cho các kì thi chọn học sinh giỏi những năm tiếp theo.
I. Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
Câu 1 - Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
Một cầu thủ bóng chày ném một quả bóng (Hình 1), anh ta nắm quả bóng và tăng tốc nó trên đoạn đường dài 50 cm từ trạng thái đứng yên đến khi đạt tốc độ 150 km/h thì bóng rời tay (tốc độ thường đạt được ở môn thể thao này). Xem lực tác dụng lên bóng không đổi cả hướng và độ lớn, quãng đường tăng tốc của bóng được xem là thẳng và hợp với phương ngang một góc 15° chếch lên trên. Lấy $g = 9.81\ \mathrm{m/s^2}$. Bỏ qua sức cản không khí.
Với quả bóng có khối lượng tiêu chuẩn 142 g, tính độ lớn lực mà tay cầu thủ tác dụng lên bóng.
Biết sau 2,35 s tính từ lúc rời tay cầu thủ thì quả bóng chạm đất. Tính tốc độ của bóng ngay trước khi chạm đất.
Câu 2 - Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
Một quả cầu kim loại lớn có khối lượng 350 kg được treo vào cần cẩu bằng một sợi cáp, khoảng cách từ đầu trên của cáp đến tâm quả cầu là 6 m (Hình 2.1). Để phá đổ một bức tường, quả cầu được kéo ra khỏi vị trí sát tường (vị trí dây cáp thẳng đứng) rồi thả ra. Cần cẩu không chuyển động.
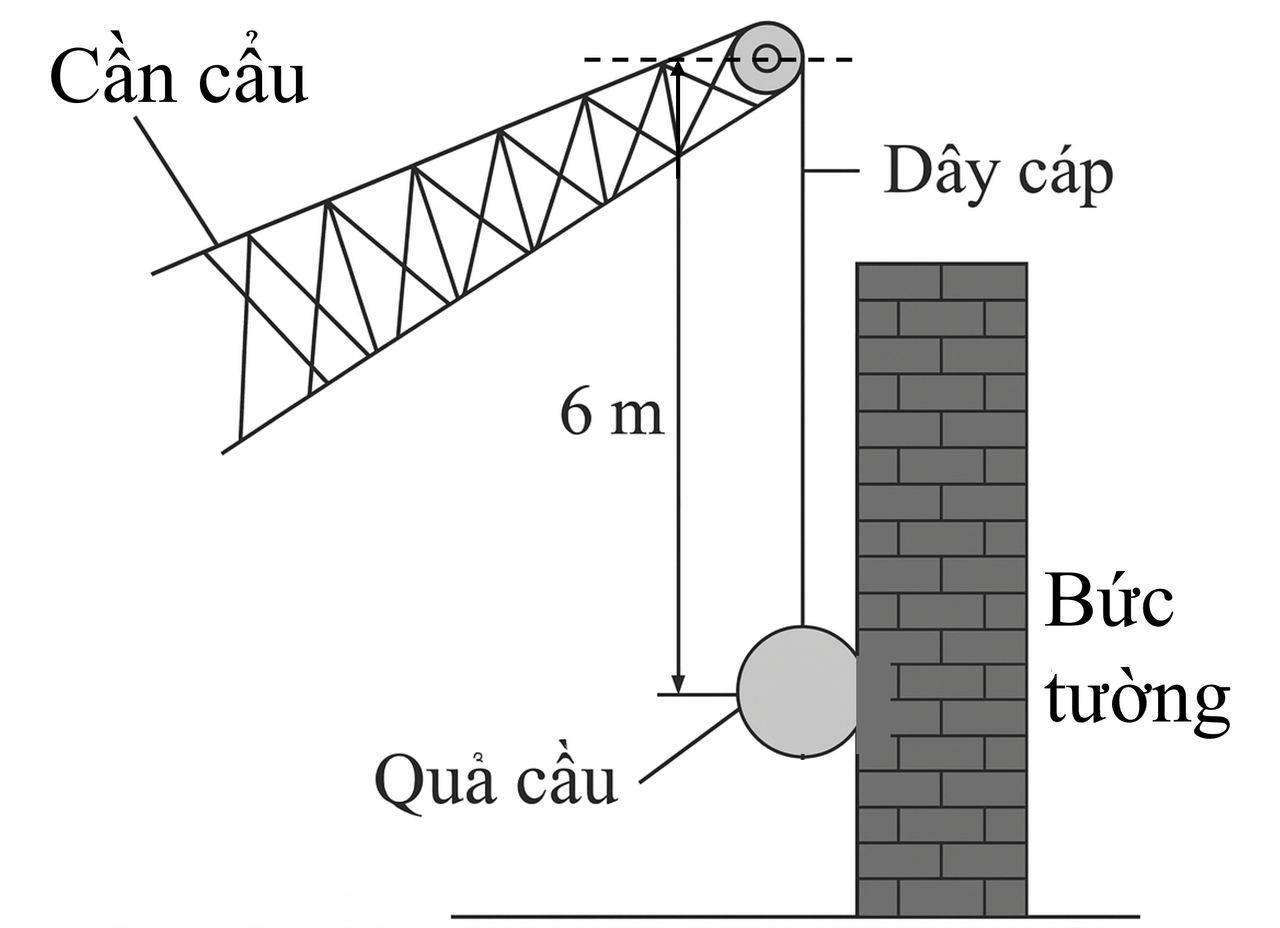
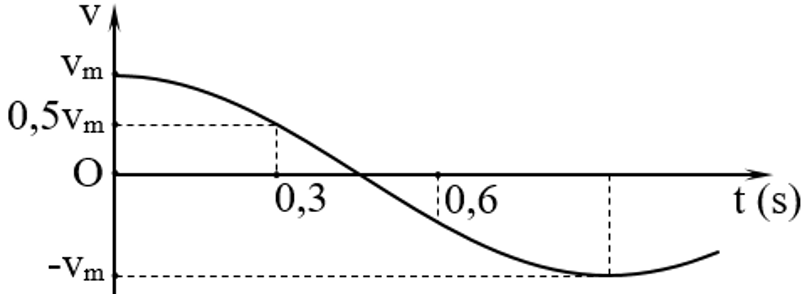
Đồ thị dưới đây biểu diễn sự biến thiên tốc độ v của quả cầu sau khi thả theo thời gian t (Hình 2.2). Đoạn đồ thị OA ứng với giai đoạn từ khi quả cầu được thả đến khi nó bắt đầu tiếp xúc với bức tường (lúc dây cáp thẳng đứng). Đoạn đồ thị AB ứng với giai đoạn quả cầu va chạm với tường. Lấy $g = 9.81\ \mathrm{m\!/\!s^2}$.
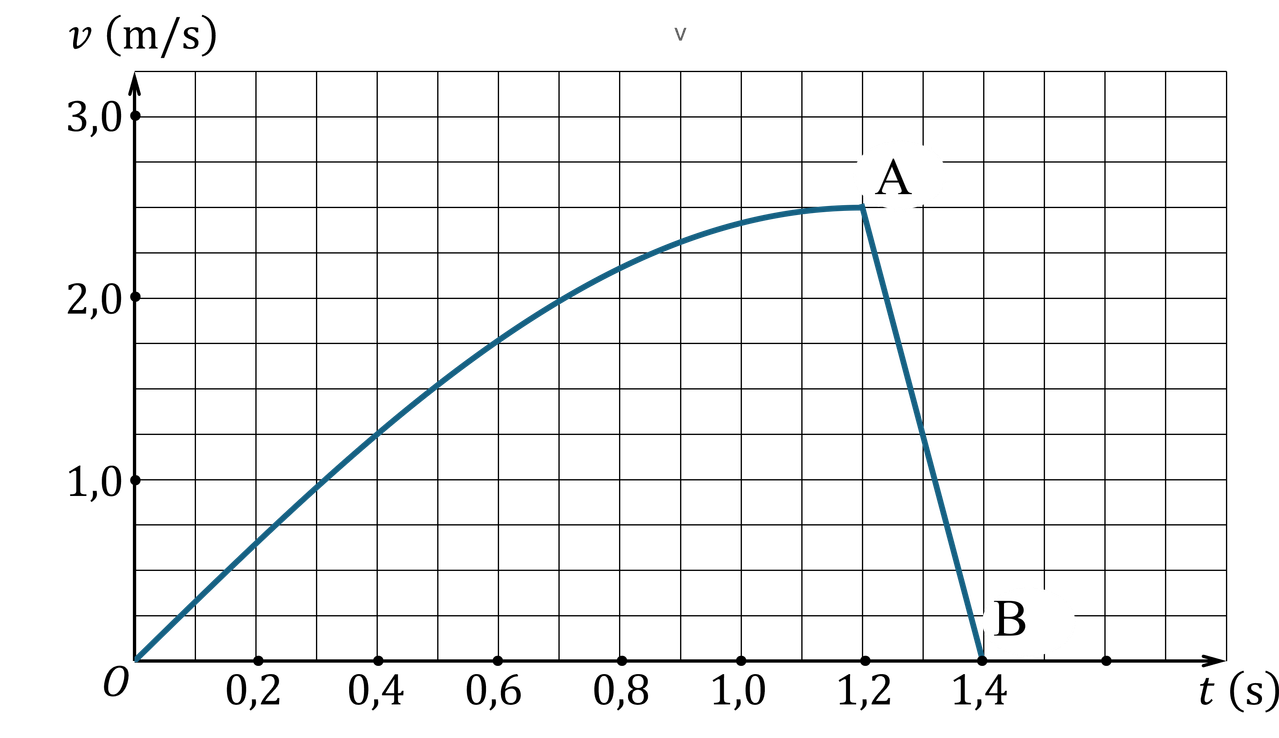
Xem chuyển động của quả cầu trong quá trình va chạm với tường là chuyển động thẳng. Tính quãng đường và tính độ biến thiên động lượng của quả cầu trong quá trình va chạm.
Tính lực căng dây cáp ngay khi quả cầu vừa chạm tường.
Câu 3 - Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
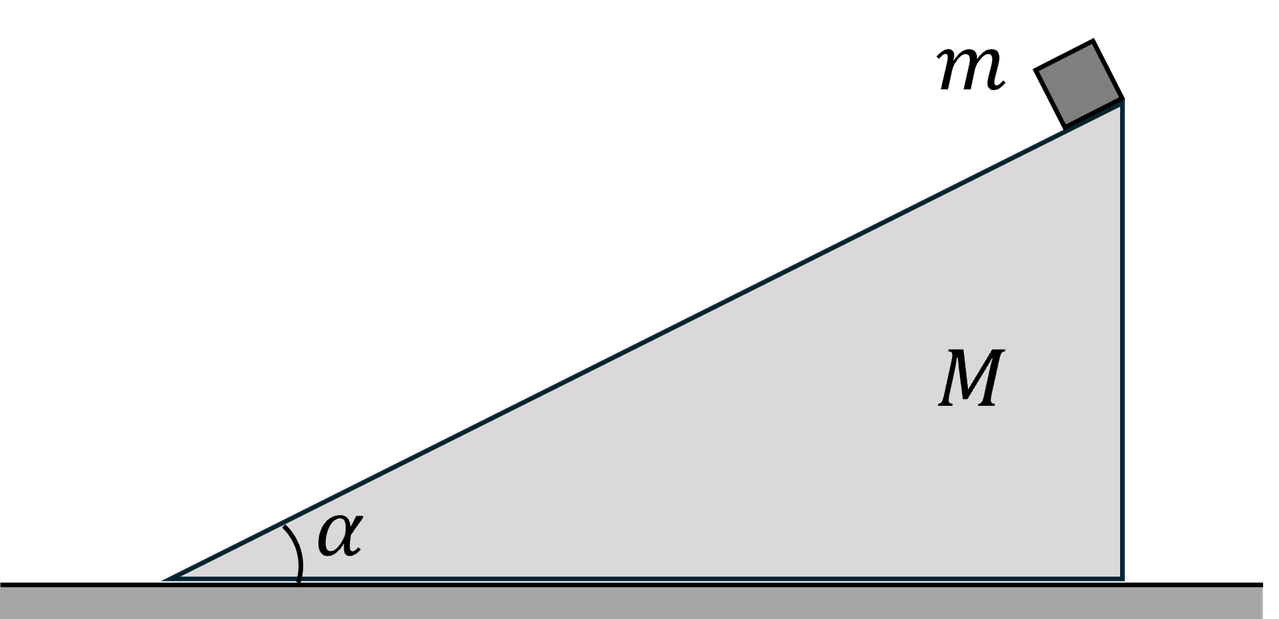
Một cái nêm có khối lượng $M$, góc nghiêng $α$, ban đầu nằm yên trên mặt sàn nằm ngang. Một vật nhỏ khối lượng $m$ được giữ nằm yên trên mặt nghiêng sát đỉnh nêm, ở độ cao $h$ so với sàn (Hình 3). Bỏ qua mọi ma sát. Tại một thời điểm nào đó ta thôi giữ vật và nêm. Tìm tốc độ của nêm khi vật nhỏ vừa đến chân nêm theo $M$, $m$, $h$, $α$ và gia tốc rơi tự do $g$.
Câu 4 - Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
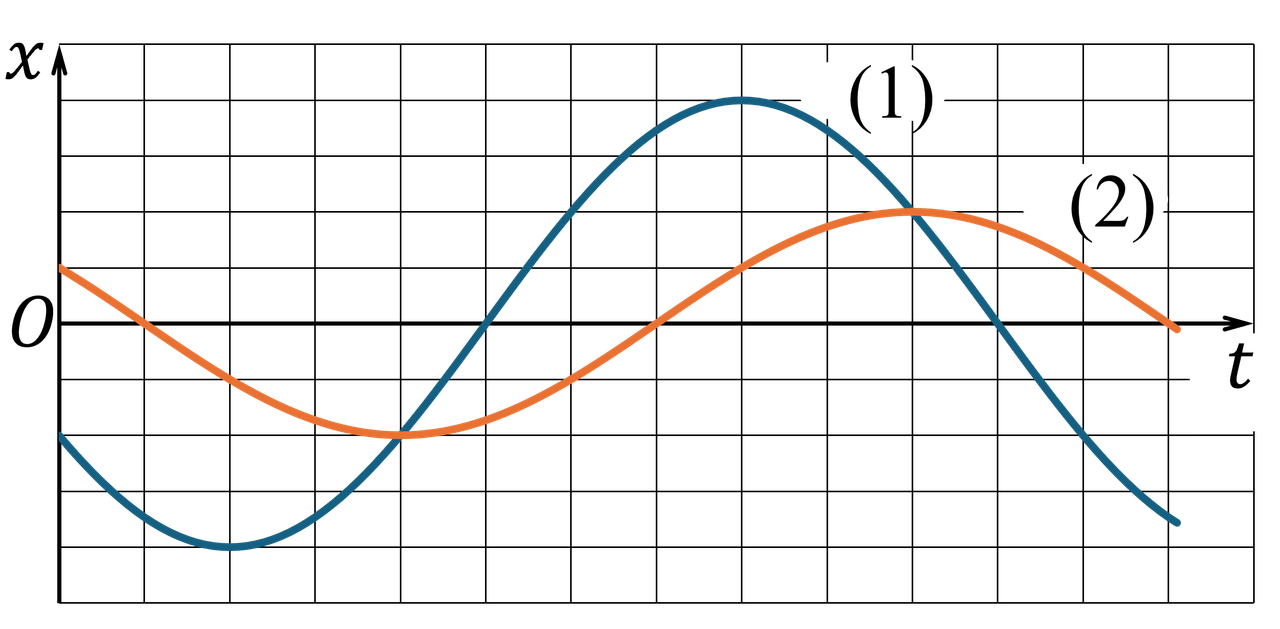
Hai vật A và B đang dao động điều hòa cùng tần số.Đồ thị biểu diễn li độ $x$ của hai vật A, B theo thời gian $t$ lần lượt là đường (1) và (2) như hình vẽ (Hình 4). Biết khối lượng của A gấp hai lần khối lượng của B. Mốc thế năng của mỗi vật được chọn ở vị trí cân bằng của chúng.
Tính tỉ số giữa cơ năng của A và cơ năng của B.
Tính độ lớn độ lệch pha giữa hai dao động.
Tính từ thời điểm mà động năng của A cực đại, sau $\dfrac{1}{10}$ chu kì dao động thì tỉ số giữa thế năng của A và thế năng của B bằng bao nhiêu?
Câu 5 - Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
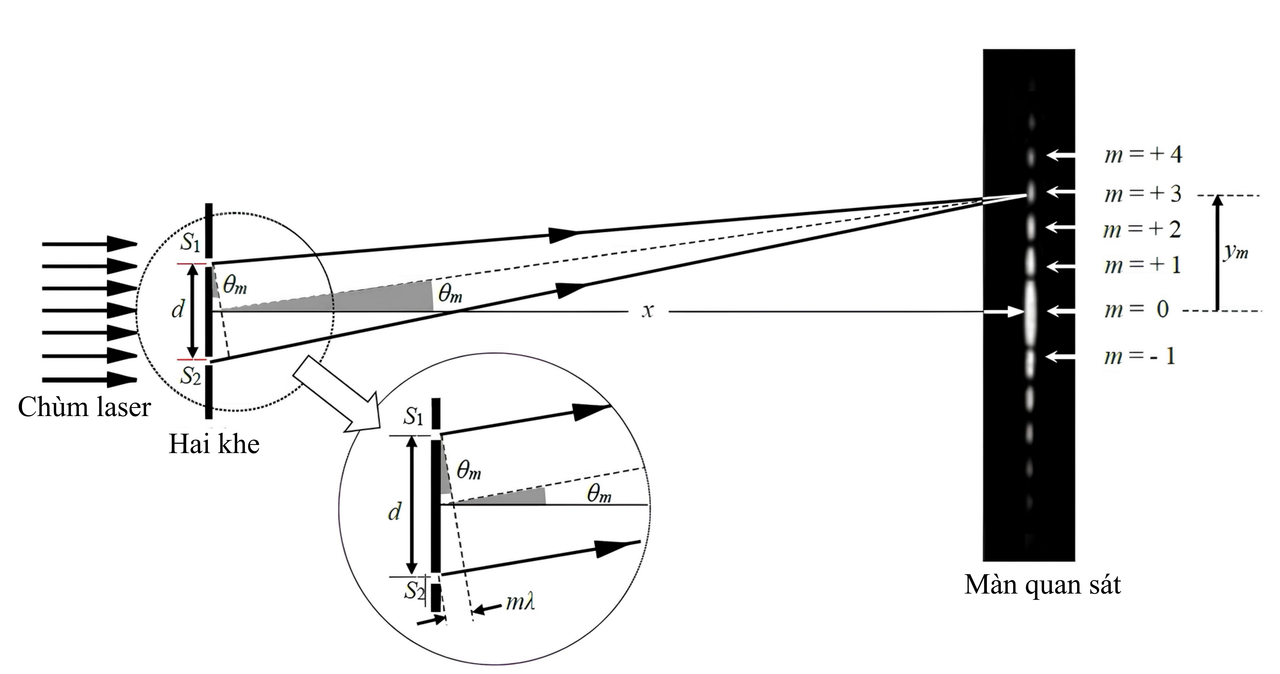
Để đo bước sóng truyền trên mặt nước, một bạn học sinh cho quả bóng tennis dao động điều hòa theo phương thẳng đứng chạm vào mặt nước (nguồn sóng) để tạo ra sóng (Hình 5.1). Trên mặt hồ có một cái phao, đo khoảng cách từ phao đến nguồn khi chưa có sóng được 12 m. Dùng đồng hồ đo được thời gian phao thực hiện 30 dao động là 24 s, thời gian từ khi nguồn bắt đầu dao động đến khi phao bắt đầu dao động là 10 s.
Tính bước sóng của sóng truyền trên mặt hồ.
Trên mặt hồ có hai cái phao nhỏ A và B ở trên cùng một phương truyền sóng. Tại thời điểm $t_1$ hình ảnh mặt nước với các phao như hình vẽ (Hình 5.2), A đang chuyển động hướng lên trên. Đường nét đứt biểu diễn mặt nước khi không có sóng. Khoảng cách từ B đến đường nét đứt bằng một nửa biên độ sóng. Tính thời gian ngắn nhất tính từ $t_1$ để khoảng cách giữa A và B bằng $0\text{,}56\ \text{m}$.
Câu 6 - Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
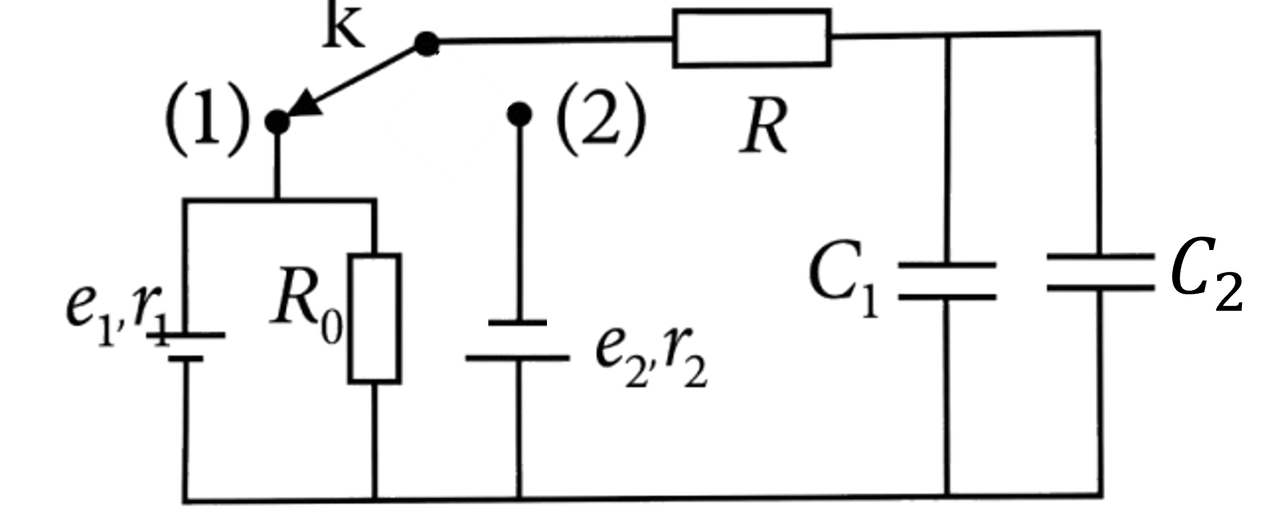
Cho mạch điện như hình vẽ (Hình 6). Các nguồn điện có suất điện động $e_1 = 3.6\ \text{V}$, $e_2 = 6\ \text{V}$, điện trở trong $r_1 = r_2 = 2\ \text{Ω}$. Các điện trở $R_0 = R = 10\ \text{Ω}$. Các tụ điện có điện dung $C_1 = 1\ \text{μF}$, $C_2 = 2\ \text{μF}$. Bỏ qua điện trở các dây nối và khóa K. Bỏ qua sự mất mát năng lượng do bức xạ sóng điện từ. Ban đầu khóa K ở vị trí (1).
Tính hiệu điện thế giữa hai cực của nguồn điện $e_1$ và tính tổng năng lượng của các tụ điện.
Tính điện lượng chạy qua $R$ và tính nhiệt năng sinh ra trên $R$ sau khi khóa K chuyển sang vị trí (2).
Câu 7 - Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
Một nhóm học sinh tiến hành thí nghiệm đo nhiệt hoá hơi riêng của nước. Các bạn đã rót 400 g nước ở nhiệt độ phòng 25 °C vào một ấm điện như hình vẽ (Hình 7.1). Các thông số kĩ thuật của ấm điện được cho như Bảng 1.
Hình 7.1. Ấm điện
|
Dung tích | 2000 mℓ |
|---|---|---|
| Điện áp | 220 V – 50Hz | |
| Công suất |
2500 W khi nước chưa sôi 1700 W khi nước sôi |
|
| Chế độ an toàn | Tự hạ công suất khi nước sôi và tự ngắt khi cạn nước | |
| Chất liệu | Vỏ ấm bằng thuỷ tinh có khả năng cách nhiệt tốt, đế ấm bằng inox 304 |
Ngoài ra, học sinh còn dùng cân điện tử để cân lượng nước còn lại trong ấm và dùng đồng hồ để đo thời gian đun. Xem nước sôi ở 100 °C, khi nước sôi thì nắp ấm được mở cho hơi nước bay ra. Khi lượng nước còn lại trong ấm là 350 g thì các bạn học sinh bắt đầu ghi lại số liệu thí nghiệm của quá trình tiếp theo. Đồ thị biểu diễn sự phụ thuộc của khối lượng nước m còn lại trong ấm vào thời gian đun τ như hình vẽ (Hình 7.2).
Biết rằng khi nước chưa sôi thì hiệu suất đun nước của ấm bằng 96 %, còn khi nước sôi thì hiệu suất đun nước giảm xuống còn 90 %. Nhiệt dung riêng của nước là 4200 J/(kg.K). Bỏ qua sự bay hơi của nước trước khi sôi.
Tính nhiệt hoá hơi riêng của nước trong thí nghiệm này.
Tính thời gian từ khi bắt đầu đun đến khi nước trong ấm hoá hơi hoàn toàn.
Câu 8 - Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
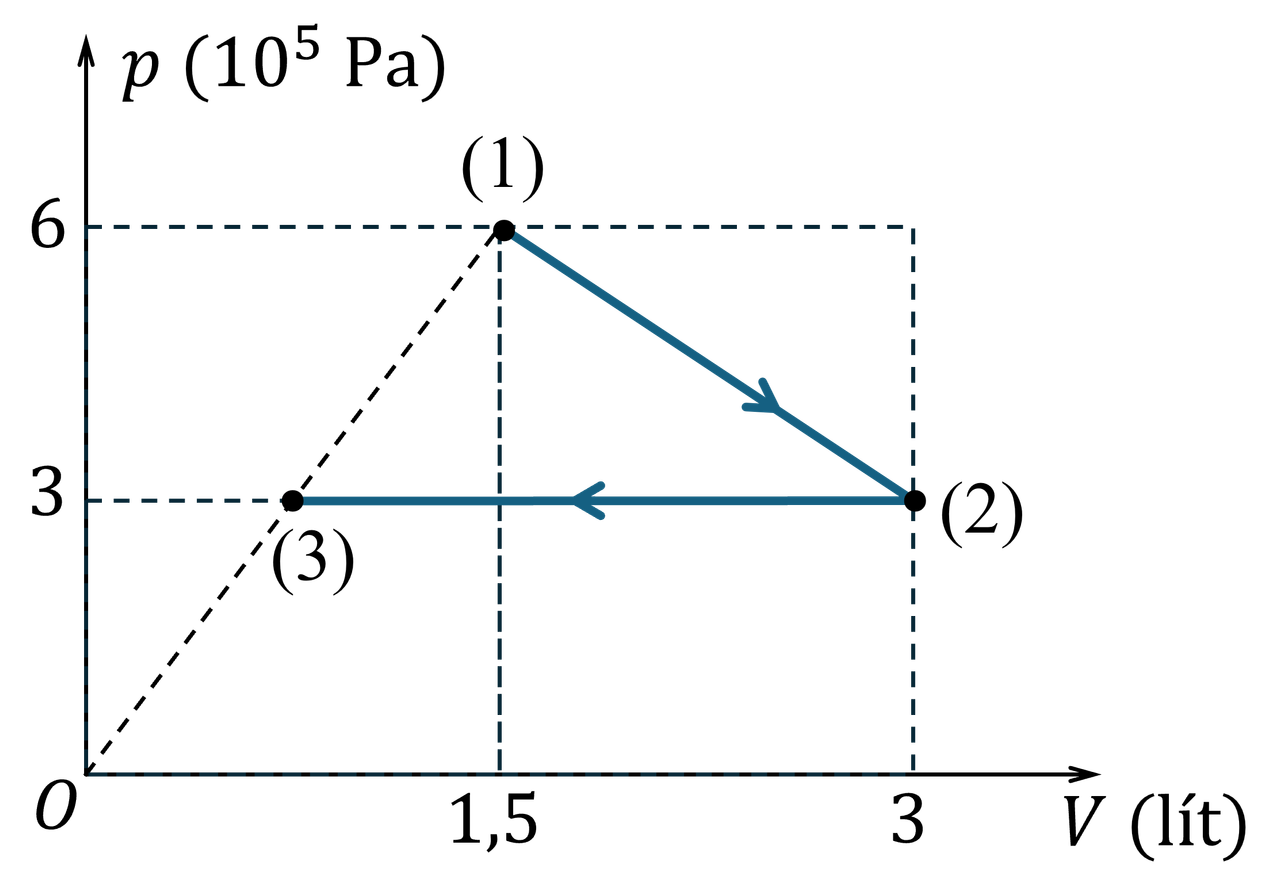
Cho 0,1 mol khí helium chứa trong một xilanh được đậy kín bởi một pit-tông (pit-tông có thể dịch chuyển không ma sát). Khối khí thực hiện quá trình biến đổi trạng thái từ (1) → (2) → (3) theo đồ thị như hình vẽ (Hình 8). Xem khí trong xilanh trong cả quá trình là khí lí tưởng, $R = 8.31\ \mathrm{J\!/\!(K\!\cdot\!mol)}$.
Tính $T_1$, $T_2$, $T_3$.
Tính độ lớn công mà khí thực hiện hay nhận được trong quá trình (1) → (2) và (2) → (3).
Tính tỉ số giữa động năng tịnh tiến trung bình cực đại và cực tiểu của nguyên tử khí helium trong cả quá trình trên.
II. Lời giải chi tiết (Đáp án) Đề thi HSG Vật lí 12 tỉnh Quảng Trị 2025 - 2026
Câu 1 (2,0 điểm)
Cho quãng đường tăng tốc $s = 50\,\text{cm} = 0{,}5\,\text{m}$, vận tốc khi rời tay $v_0 = 150\,\text{km/h}$, góc ném $\alpha = 15^\circ$, $g = 9{,}81\,\text{m/s}^2$, khối lượng bóng $m = 142\,\text{g} = 0{,}142\,\text{kg}$. Bỏ qua lực cản không khí.
1) Tính độ lớn lực tay cầu thủ tác dụng lên bóng
Đổi đơn vị vận tốc:
$$v_0 = 150\,\text{km/h} = 150\cdot\frac{1000}{3600}\,\text{m/s} \approx 41{,}67\,\text{m/s}.$$Trong giai đoạn tăng tốc, bóng chuyển động thẳng nhanh dần đều nên dùng hệ thức $v_0^2 = 2as$:
$$\begin{align} a &= \frac{v_0^2}{2s} = \frac{(41{,}67)^2}{2\cdot 0{,}5} \approx 1736\,\text{m/s}^2. \end{align}$$Áp dụng định luật II Newton (lấy độ lớn):
$$\begin{align} F &= ma = 0{,}142 \cdot 1736 \approx 2{,}47\times 10^2\,\text{N}. \end{align}$$Kết luận: $F \approx 247\,\text{N}$.
2) Tính tốc độ của bóng ngay trước khi chạm đất
Sau khi rời tay, bóng chuyển động ném xiên. Tách vận tốc ban đầu theo hai trục:
$$v_{0x} = v_0\cos 15^\circ,\qquad v_{0y} = v_0\sin 15^\circ.$$Sau thời gian $t = 2{,}35\,\text{s}$, ta có:
$$v_x = v_{0x},\qquad v_y = v_{0y} - gt.$$Do đó tốc độ ngay trước khi chạm đất:
$$\begin{align} v &= \sqrt{v_x^2 + v_y^2}\\ &= \sqrt{(v_0\cos 15^\circ)^2 + (v_0\sin 15^\circ - gt)^2}. \end{align}$$Thay số $v_0 \approx 41{,}67\,\text{m/s}$, $g = 9{,}81\,\text{m/s}^2$, $t = 2{,}35\,\text{s}$:
$$\begin{align} v &\approx \sqrt{(41{,}67\cos 15^\circ)^2 + (41{,}67\sin 15^\circ - 9{,}81\cdot 2{,}35)^2}\\ &\approx 42{,}0\,\text{m/s}. \end{align}$$Kết luận: $v \approx 42{,}0\,\text{m/s}$.
Câu 2 (2,5 điểm)
Dữ kiện: $m=350\,\text{kg}$, $L=6\,\text{m}$, $g=9{,}81\,\text{m/s}^2$. Từ đồ thị $v(t)$ (Hình 2.2) đọc được tại thời điểm bắt đầu chạm tường (điểm $A$): $t_A \approx 1{,}2\,\text{s}$, $v_A \approx 2{,}5\,\text{m/s}$; kết thúc va chạm (điểm $B$): $t_B \approx 1{,}4\,\text{s}$, $v_B \approx 0\,\text{m/s}$. Do đó $\Delta t = t_B-t_A \approx 0{,}2\,\text{s}$.
1) Quãng đường và độ biến thiên động lượng trong quá trình va chạm
Trong giai đoạn va chạm $AB$, xem chuyển động thẳng và do đoạn $AB$ là đoạn thẳng trên đồ thị $v-t$ nên $v$ biến thiên tuyến tính theo $t$. Khi đó quãng đường trong va chạm bằng diện tích hình thang dưới đồ thị:
$$\begin{align} s_{AB} &= \frac{v_A+v_B}{2}\,(t_B-t_A) = \frac{v_A+v_B}{2}\,\Delta t. \end{align}$$Thay số $v_A\approx 2{,}5$, $v_B\approx 0$, $\Delta t\approx 0{,}2$:
$$\begin{align} s_{AB} &\approx \frac{2{,}5+0}{2}\cdot 0{,}2 = 0{,}25\,\text{m}. \end{align}$$Độ biến thiên động lượng trong va chạm (lấy độ lớn), vì tốc độ giảm từ $v_A$ về $0$:
$$\begin{align} |\Delta \vec p| &= m\,| \vec v_B-\vec v_A| = m\,(v_A-v_B) \approx m\,v_A. \end{align}$$ $$\begin{align} |\Delta \vec p| &\approx 350\cdot 2{,}5 = 875\,\text{kg·m/s}. \end{align}$$Kết quả: $s_{AB}\approx 0{,}25\,\text{m}$, $|\Delta \vec p|\approx 875\,\text{kg·m/s}$.
2) Lực căng dây cáp ngay khi quả cầu vừa chạm tường
Thời điểm “vừa chạm tường” là lúc dây cáp thẳng đứng (điểm $A$), quả cầu ở vị trí thấp nhất nên gia tốc hướng tâm có độ lớn $a_h = \dfrac{v_A^2}{L}$ hướng lên theo dây. Chiếu theo phương dây (hướng lên dương):
$$\begin{align} T - mg &= m\frac{v_A^2}{L}. \end{align}$$ $$\begin{align} T &= mg + m\frac{v_A^2}{L}. \end{align}$$Thay số $m=350$, $g=9{,}81$, $L=6$, $v_A\approx 2{,}5$:
$$\begin{align} T &\approx 350\cdot 9{,}81 + 350\cdot\frac{(2{,}5)^2}{6} \approx 3{,}80\times 10^3\,\text{N}. \end{align}$$Kết quả: $T \approx 3{,}8\,\text{kN}$.
Câu 3 (1,5 điểm)
Xét hệ gồm nêm (khối lượng $M$) và vật nhỏ (khối lượng $m$) trên mặt sàn nhẵn, bỏ qua mọi ma sát. Ban đầu hệ đứng yên. Khi thả, vật nhỏ trượt từ độ cao $h$ xuống chân nêm. Cần tìm tốc độ của nêm đúng lúc vật vừa đến chân nêm.
1) Bảo toàn động lượng theo phương ngang
Chọn chiều dương sang phải. Gọi $V$ là tốc độ của nêm so với đất tại thời điểm vật tới chân nêm. Gọi $u$ là tốc độ của vật so với nêm dọc theo mặt phẳng nghiêng (hướng xuống). Vì nêm trượt trên sàn không ma sát nên ngoại lực theo phương ngang bằng $0$, suy ra động lượng theo phương ngang được bảo toàn.
Khi vật trượt xuống theo mặt nghiêng, thành phần vận tốc của vật theo phương ngang (trong hệ quy chiếu mặt đất) có dạng $v_x = V - u\cos\alpha$ (vì vật trượt xuống về phía chân nêm, ngược chiều dương ngang). Do đó:
$$\begin{align} MV + m(V-u\cos\alpha) &= 0. \end{align}$$ $$\begin{align} (M+m)V &= m\,u\cos\alpha \quad\Rightarrow\quad V &= \frac{m\,u\cos\alpha}{M+m}. \end{align}$$2) Bảo toàn cơ năng
Thế năng của vật giảm một lượng $mgh$ (vì vật hạ thấp đúng $h$). Cơ năng chuyển hết thành động năng của cả nêm và vật (không có ma sát).
Tốc độ của vật so với đất có: $v_y = u\sin\alpha$ (hướng xuống) và $v_x = V-u\cos\alpha$, nên:
$$\begin{align} v^2 &= (V-u\cos\alpha)^2 + (u\sin\alpha)^2 = V^2 -2Vu\cos\alpha + u^2. \end{align}$$Viết phương trình bảo toàn cơ năng:
$$\begin{align} mgh &= \frac12 MV^2 + \frac12 m v^2. \end{align}$$Thay $v^2$ và $V=\dfrac{m\,u\cos\alpha}{M+m}$ vào, rút gọn được:
$$\begin{align} u^2 &= \frac{2gh\,(M+m)}{M+m - m\cos^2\alpha} = \frac{2gh\,(M+m)}{M + m\sin^2\alpha}. \end{align}$$Suy ra tốc độ của nêm:
$$\begin{align} V &= \frac{m\cos\alpha}{M+m}\,\sqrt{u^2} = \frac{m\cos\alpha}{M+m}\sqrt{\frac{2gh\,(M+m)}{M+m-m\cos^2\alpha}}. \end{align}$$Viết gọn:
$$\begin{align} V &= m\cos\alpha\;\sqrt{\frac{2gh}{(M+m)\,(M+m\sin^2\alpha)}}. \end{align}$$Kết luận: tốc độ của nêm khi vật vừa đến chân nêm là $V = m\cos\alpha\sqrt{\dfrac{2gh}{(M+m)(M+m\sin^2\alpha)}}$.
Câu 4 (3,0 điểm)
Hai vật $A,B$ dao động điều hòa cùng tần số (cùng $\omega$). Từ đồ thị Hình 4 ta đọc được: biên độ của (1) (vật $A$) gấp đôi biên độ của (2) (vật $B$), tức là $A_A = 2A_B$; đồng thời $m_A = 2m_B$.
1) Tỉ số cơ năng $\dfrac{E_A}{E_B}$
Với dao động điều hòa: $E=\dfrac12 m\omega^2 A^2$ (mốc thế năng tại VTCB). Do hai vật cùng tần số nên cùng $\omega$:
$$\begin{align} \frac{E_A}{E_B} &= \frac{\frac12 m_A\omega^2 A_A^2}{\frac12 m_B\omega^2 A_B^2} = \frac{m_A}{m_B}\cdot\left(\frac{A_A}{A_B}\right)^2. \end{align}$$Thay $m_A=2m_B$ và $A_A=2A_B$:
$$\begin{align} \frac{E_A}{E_B} &= 2\cdot 2^2 = 8. \end{align}$$Kết luận: $\dfrac{E_A}{E_B}=8$.
2) Độ lệch pha giữa hai dao động
Từ đồ thị, ta lấy hai đỉnh liên tiếp (hoặc hai lần qua VTCB cùng chiều) để xác định chu kì $T$. Đồng thời đo độ lệch thời gian $\Delta t$ giữa hai trạng thái tương ứng của hai đường (1) và (2) (ví dụ: thời điểm đạt cực đại). Khi đó:
$$\begin{align} \Delta\varphi &= \omega\Delta t = \frac{2\pi}{T}\,\Delta t. \end{align}$$Đọc trên Hình 4, độ lệch theo trục thời gian giữa hai đỉnh tương ứng bằng $\Delta t = \dfrac{T}{6}$, nên:
$$\begin{align} \Delta\varphi &= \frac{2\pi}{T}\cdot\frac{T}{6} = \frac{\pi}{3}. \end{align}$$Kết luận: $\Delta\varphi=\dfrac{\pi}{3}$.
3) Tỉ số thế năng của A và B sau $\dfrac{1}{10}T$
Tại thời điểm $t_0$ khi động năng của $A$ cực đại thì $x_A(t_0)=0$. Sau khoảng thời gian $\Delta t=\dfrac{T}{10}$, quan sát trực tiếp trên đồ thị Hình 4, đọc được độ lớn li độ của hai vật thỏa mãn xấp xỉ:
$$\frac{x_A}{x_B}\approx 2{,}9.$$Với dao động điều hòa, thế năng đàn hồi có dạng $U=\dfrac12 kx^2$. Do hai vật dao động cùng tần số nên $k=m\omega^2$, suy ra:
$$\begin{align} \frac{U_A}{U_B} &= \frac{k_A}{k_B}\left(\frac{x_A}{x_B}\right)^2 = \frac{m_A}{m_B}\left(\frac{x_A}{x_B}\right)^2. \end{align}$$Vì $m_A=2m_B$, ta được:
$$\begin{align} \frac{U_A}{U_B} &= 2\cdot (2{,}9)^2 \approx 16{,}8. \end{align}$$Kết luận: $\dfrac{U_A}{U_B}\approx 16{,}8$.
Câu 5 (2,5 điểm)
Dữ kiện: khoảng cách từ nguồn đến phao $d=12\,\text{m}$; thời gian sóng truyền tới phao $t=10\,\text{s}$; thời gian phao thực hiện $30$ dao động là $24\,\text{s}$.
1) Bước sóng của sóng truyền trên mặt hồ
Chu kì và tần số:
$$T=\frac{24}{30}=0{,}8\,\text{s},\qquad f=\frac1T=1{,}25\,\text{Hz}.$$Vận tốc truyền sóng:
$$v=\frac{d}{t}=\frac{12}{10}=1{,}2\,\text{m/s}.$$Bước sóng:
$$\lambda=\frac{v}{f}=\frac{1{,}2}{1{,}25}=0{,}96\,\text{m}.$$Kết luận: $\lambda=0{,}96\,\text{m}$.
2) Thời gian ngắn nhất kể từ $t_1$ để $AB=0{,}56\,\text{m}$
Từ đường tròn pha suy ra độ lệch pha giữa hai phao tại cùng thời điểm là $\Delta\varphi=\dfrac{7\pi}{6}$, nên độ lệch theo phương truyền sóng:
$$\Delta x=\frac{\Delta\varphi}{2\pi}\lambda=\frac{7}{12}\lambda.$$Với $\lambda=0{,}96\,\text{m}$:
$$\Delta x=\frac{7\cdot 0{,}96}{12}=0{,}56\,\text{m}.$$Khoảng cách hình học giữa hai phao:
$$AB=\sqrt{(\Delta x)^2+(\Delta u)^2}.$$Thay $AB=0{,}56\,\text{m}$:
$$\begin{align} (AB)^2 &= \left(\frac{7\cdot 0{,}96}{12}\right)^2+(\Delta u)^2\\ (0{,}56)^2 &= (0{,}56)^2+(\Delta u)^2\\ \Rightarrow\ (\Delta u)^2 &= 0. \end{align}$$Suy ra $\Delta u=0$, tức là tại thời điểm cần tìm thì hai phao ở cùng độ cao ($u_A=u_B$). Dùng đường tròn pha suy ra thời điểm gần nhất để $A$ và $B$ cùng độ cao tương ứng với pha tăng thêm một lượng $$\Delta\phi=\frac{11\pi}{12}.$$
Khi đó:
$$\begin{align} \Delta t &= \frac{\Delta\phi}{\omega} = \frac{\frac{11\pi}{12}}{\frac{2\pi}{T}}\\ &= \frac{11}{24}T. \end{align}$$Với $T=0{,}8\,\text{s}$:
$$\Delta t=\frac{11}{24}\cdot 0{,}8\approx 0{,}367\,\text{s}.$$Kết luận: $\Delta t_{\min}\approx 0{,}367\,\text{s}$.
Câu 6 (2,5 điểm)
Cho $e_1=3{,}6\,\text{V}$, $e_2=6\,\text{V}$, $r_1=r_2=2\,\Omega$, $R_0=R=10\,\Omega$, $C_1=1\,\mu\text{F}$, $C_2=2\,\mu\text{F}$. Bỏ qua điện trở dây và khóa k. Ban đầu k ở vị trí (1), sau đó chuyển sang (2).
1) Hiệu điện thế hai cực nguồn $e_1$ và tổng năng lượng của các tụ điện (k ở (1))
Ở trạng thái ổn định một chiều, dòng qua nhánh tụ bằng 0 nên dòng chỉ chạy qua mạch $e_1, r_1$ và $R_0$. Khi đó:
$$\begin{align} I_1 &= \frac{e_1}{r_1+R_0} = \frac{3{,}6}{2+10} = 0{,}3\,\text{A}. \end{align}$$Hiệu điện thế giữa hai cực nguồn $e_1$ (điện áp mạch ngoài) chính là điện áp trên $R_0$:
$$\begin{align} U_1 &= I_1R_0 = 0{,}3\cdot 10 = 3{,}0\,\text{V}. \end{align}$$Hai tụ $C_1, C_2$ mắc song song nên $C_{\text{eq}}=C_1+C_2=3\,\mu\text{F}$. Ở trạng thái ổn định, điện áp trên tụ bằng điện áp nút mạch nên $U_C=U_1=3{,}0\,\text{V}$. Tổng năng lượng các tụ:
$$\begin{align} W_C &= \frac12 C_{\text{eq}}U_C^2\\ &= \frac12\cdot 3\cdot 10^{-6}\cdot (3{,}0)^2\\ &= 13{,}5\times 10^{-6}\,\text{J} = 13{,}5\,\mu\text{J}. \end{align}$$Kết quả: $U_1=3{,}0\,\text{V}$; $W_C=13{,}5\,\mu\text{J}$.
2) Điện lượng qua $R$ và nhiệt lượng tỏa trên $R$ khi chuyển k sang (2)
Khi chuyển k sang (2), bản tụ phía trên được nối với cực còn lại của nguồn $e_2$ nên điện tích trên các bản bị đổi dấu (so với trạng thái khi k ở (1)). Gọi $q_1,q_2$ là điện tích (theo dấu quy ước ban đầu) trên $C_1,C_2$ ngay trước khi chuyển k; và $q_1',q_2'$ là điện tích ngay sau khi mạch đạt trạng thái ổn định mới (k ở (2)).
Ở trạng thái ổn định, điện áp trên mỗi tụ bằng điện áp nguồn tương ứng: khi k ở (1) thì $U_0=3\,\text{V}$; khi k ở (2) thì $U_\infty=6\,\text{V}$. Do đó: $q_1=C_1U_0,\ q_2=C_2U_0$ và $q_1'=C_1U_\infty,\ q_2'=C_2U_\infty$.
Vì điện tích bị đổi dấu khi chuyển sang (2), điện lượng chạy qua nhánh $R$ chính là độ biến thiên tổng điện tích trên nút bản trên của bộ tụ:
$$\begin{align} \Delta q &= -\left(q_1'+q_2'\right)-\left(q_1+q_2\right)\\ &= -\left(C_1U_\infty+C_2U_\infty\right)-\left(C_1U_0+C_2U_0\right)\\ &= -(C_1+C_2)\left(U_\infty+U_0\right). \end{align}$$Lấy độ lớn điện lượng qua $R$:
$$\begin{align} Q_R &=|\Delta q| =(C_1+C_2)\left(U_\infty+U_0\right)\\ &=(1+2)\cdot 10^{-6}\,(6+3)\\ &=27\times 10^{-6}\,\text{C} =27\,\mu\text{C}. \end{align}$$Công của nguồn $e_2$ trong quá trình (theo độ lớn):
$$\begin{align} A &= e_2\,Q_R\\ &= 6\cdot 27\times 10^{-6}\\ &=162\,\mu\text{J}. \end{align}$$Độ biến thiên năng lượng của bộ tụ:
$$\begin{align} \Delta W_C &=\frac12(C_1+C_2)\left(U_\infty^2-U_0^2\right)\\ &=\frac12\cdot 3\cdot 10^{-6}\,(36-9)\\ &=40{,}5\,\mu\text{J}. \end{align}$$Nhiệt lượng tỏa ra trên các điện trở của mạch khi nạp lại:
$$\begin{align} Q_{\text{tỏa}} &=A-\Delta W_C\\ &=162-40{,}5\\ &=121{,}5\,\mu\text{J}. \end{align}$$Do $R$ nối tiếp với $r_2$ nên nhiệt phân bố theo tỉ lệ điện trở:
$$\begin{align} Q_R^{(\text{nhiệt})} &=\frac{R}{R+r_2}\,Q_{\text{tỏa}}\\ &=\frac{10}{10+2}\cdot 121{,}5\\ &=101{,}25\,\mu\text{J}. \end{align}$$Kết quả: $Q_R=27\,\mu\text{C}$; nhiệt lượng tỏa trên $R$ là $101{,}25\,\mu\text{J}$.
Câu 7 (3,0 điểm)
Dữ kiện: $m_0=400\,\text{g}=0{,}4\,\text{kg}$ ở $25^\circ\text{C}$, $c=4200\,\text{J/(kg.K)}$, nước sôi ở $100^\circ\text{C}$, bỏ qua sự bay hơi trước khi sôi. Ấm điện: $P_1=2500\,\text{W}$ (khi chưa sôi), $\eta_1=96\%$; $P_2=1700\,\text{W}$ (khi sôi), $\eta_2=90\%$. Khi nước sôi và mở nắp, bắt đầu ghi số liệu từ lúc khối lượng còn lại $350\,\text{g}$. Từ đồ thị Hình 7.2 đọc được xấp xỉ: tại $\tau=400\,\text{s}$ thì $m\approx 80\,\text{g}$.
1) Tính nhiệt hóa hơi riêng $L$ của nước trong thí nghiệm
Khi nước đang sôi (mở nắp), nhiệt lượng hữu ích dùng để hóa hơi mỗi giây: $$P_h=\eta_2P_2=0{,}9\cdot 1700=1530\,\text{W}.$$
Từ đồ thị (đoạn thẳng), tốc độ giảm khối lượng là không đổi:
$$\begin{align} \left|\frac{dm}{d\tau}\right| &\approx \frac{350-80}{400}\ \text{(g/s)}\\ &=\frac{270}{400}\ \text{(g/s)} =0{,}675\ \text{(g/s)} =6{,}75\times 10^{-4}\ \text{(kg/s)}. \end{align}$$Khi hóa hơi đều: $P_h = L\left|\dfrac{dm}{d\tau}\right|$, do đó:
$$\begin{align} L &= \frac{P_h}{\left|\frac{dm}{d\tau}\right|}\\ &= \frac{1530}{6{,}75\times 10^{-4}}\\ &\approx 2{,}27\times 10^6\,\text{J/kg}. \end{align}$$Kết luận: $L \approx 2{,}27\times 10^6\,\text{J/kg}$.
2) Thời gian từ lúc bắt đầu đun đến khi nước trong ấm hóa hơi hoàn toàn
Giai đoạn 1: đun từ $25^\circ\text{C}$ đến $100^\circ\text{C}$ cho $0{,}4\,\text{kg}$ nước. Nhiệt lượng cần:
$$\begin{align} Q_1 &= mc\Delta T\\ &= 0{,}4\cdot 4200\cdot (100-25)\\ &= 1{,}26\times 10^5\,\text{J}. \end{align}$$Công suất hữu ích khi chưa sôi: $P_{h1}=\eta_1P_1=0{,}96\cdot 2500=2400\,\text{W}$. Thời gian đun đến sôi:
$$\begin{align} t_1 &= \frac{Q_1}{P_{h1}}\\ &= \frac{1{,}26\times 10^5}{2400}\\ &\approx 52{,}5\,\text{s}. \end{align}$$Giai đoạn 2: hóa hơi toàn bộ $0{,}4\,\text{kg}$ nước ở $100^\circ\text{C}$. Với $P_h=1530\,\text{W}$ và $L$ ở trên:
$$\begin{align} t_2 &= \frac{m_0L}{P_h}\\ &= \frac{0{,}4\cdot 2{,}27\times 10^6}{1530}\\ &\approx 5{,}93\times 10^2\,\text{s}. \end{align}$$Tổng thời gian từ lúc bắt đầu đun đến khi hóa hơi hoàn toàn:
$$\begin{align} t &= t_1+t_2\\ &\approx 52{,}5+593\\ &\approx 6{,}45\times 10^2\,\text{s} \approx 10{,}8\,\text{phút}. \end{align}$$Kết luận: $t\approx 645\,\text{s}\approx 10{,}8\,\text{phút}$.
Câu 8 (3,0 điểm)
Cho $n=0{,}1\,\text{mol}$ khí He lí tưởng, $R=8{,}31\,\text{J/(K.mol)}$. Trên đồ thị $p\,(10^5\text{Pa})-V\,(\text{lít})$: $(1): (V_1=1{,}5\,\text{lít},\,p_1=6\cdot 10^5\,\text{Pa})$, $(2): (V_2=3\,\text{lít},\,p_2=3\cdot 10^5\,\text{Pa})$. Đoạn $2\to 3$ đẳng áp $p=3\cdot 10^5\,\text{Pa}$ và $(3)$ nằm trên đường thẳng nối $(1)$ với gốc tọa độ nên $\dfrac{p}{V}=\dfrac{6}{1{,}5}=4$ (theo đơn vị trên hình), do đó $V_3=\dfrac{3}{4}=0{,}75\,\text{lít}$.
1) Tính $T_1,\ T_2,\ T_3$
Dùng phương trình khí lí tưởng $pV=nRT$ với $1\,\text{lít}=10^{-3}\,\text{m}^3$.
$$\begin{align} T_1 &= \frac{p_1V_1}{nR} = \frac{6\cdot 10^5\cdot 1{,}5\cdot 10^{-3}}{0{,}1\cdot 8{,}31}\\ &\approx 1{,}08\times 10^3\,\text{K}. \end{align}$$ $$\begin{align} T_2 &= \frac{p_2V_2}{nR} = \frac{3\cdot 10^5\cdot 3\cdot 10^{-3}}{0{,}1\cdot 8{,}31}\\ &\approx 1{,}08\times 10^3\,\text{K}. \end{align}$$ $$\begin{align} T_3 &= \frac{p_3V_3}{nR} = \frac{3\cdot 10^5\cdot 0{,}75\cdot 10^{-3}}{0{,}1\cdot 8{,}31}\\ &\approx 2{,}71\times 10^2\,\text{K}. \end{align}$$Kết quả: $T_1\approx T_2\approx 1{,}08\times 10^3\,\text{K}$; $T_3\approx 2{,}71\times 10^2\,\text{K}$.
2) Công khí thực hiện (hay nhận) trong $(1)\to(2)$ và $(2)\to(3)$
Đoạn $(1)\to(2)$ là đoạn thẳng trên đồ thị nên $p$ biến thiên tuyến tính theo $V$, do đó:
$$\begin{align} W_{12} &= \frac{p_1+p_2}{2}\,(V_2-V_1)\\ &= \frac{6\cdot 10^5+3\cdot 10^5}{2}\,\bigl((3-1{,}5)\cdot 10^{-3}\bigr)\\ &= 4{,}5\cdot 10^5\cdot 1{,}5\cdot 10^{-3}\\ &= 675\,\text{J}. \end{align}$$Đoạn $(2)\to(3)$ đẳng áp $p_2=3\cdot 10^5\,\text{Pa}$:
$$\begin{align} W_{23} &= p_2\,(V_3-V_2)\\ &= 3\cdot 10^5\,\bigl((0{,}75-3)\cdot 10^{-3}\bigr)\\ &= -675\,\text{J}. \end{align}$$Kết luận: $W_{12}=+675\,\text{J}$ (khí thực hiện công); $W_{23}=-675\,\text{J}$ (khí nhận công $675\,\text{J}$).
3) Tỉ số giữa động năng tịnh tiến trung bình cực đại và cực tiểu của nguyên tử He
Với khí lí tưởng đơn nguyên tử, động năng tịnh tiến trung bình tỉ lệ với nhiệt độ tuyệt đối: $\overline{E_k}=\dfrac{3}{2}kT \Rightarrow \dfrac{\overline{E_{k,\max}}}{\overline{E_{k,\min}}}=\dfrac{T_{\max}}{T_{\min}}$.
Trên đoạn $(1)\to(2)$: phương trình đường thẳng (theo đơn vị trên hình) là $p=9-2V$ nên $pV=9V-2V^2$ đạt cực đại tại $V=\dfrac{9}{4}=2{,}25\,\text{lít}$.
$$\begin{align} (pV)_{\max} &= 9\cdot 2{,}25-2\cdot (2{,}25)^2\\ &= 10{,}125\ \bigl(10^5\text{Pa}\cdot \text{lít}\bigr). \end{align}$$Còn $(pV)_{\min}$ nằm tại trạng thái (3): $(pV)_{\min}=3\cdot 0{,}75=2{,}25\ \bigl(10^5\text{Pa}\cdot \text{lít}\bigr)$. Do đó:
$$\begin{align} \frac{\overline{E_{k,\max}}}{\overline{E_{k,\min}}} &= \frac{T_{\max}}{T_{\min}} = \frac{(pV)_{\max}}{(pV)_{\min}}\\ &= \frac{10{,}125}{2{,}25} = 4{,}5 = \frac{9}{2}. \end{align}$$Kết luận: $\dfrac{\overline{E_{k,\max}}}{\overline{E_{k,\min}}}=\dfrac{9}{2}$.
Qua việc giải chi tiết các câu hỏi, có thể thấy đề thi học sinh giỏi Vật lí 12 tỉnh Quảng Trị năm học 2025 – 2026 có mức độ phân hóa rõ ràng, yêu cầu học sinh nắm vững kiến thức cơ bản đồng thời vận dụng linh hoạt các phương pháp phân tích và tư duy vật lí. Các bài toán gắn với hiện tượng thực tế, đồ thị và thí nghiệm giúp đánh giá chính xác năng lực lập luận, kĩ năng xử lí số liệu cũng như khả năng tổng hợp kiến thức của thí sinh. Bộ lời giải trên hi vọng sẽ là tài liệu tham khảo hữu ích cho giáo viên và học sinh trong quá trình ôn luyện và bồi dưỡng học sinh giỏi.
