
Vượt qua gai góc để đến vì sao
“Nhân loại sẽ rời khỏi Trái Đất trong vòng chưa đầy 600 năm… Chúng ta đang cạn kiệt không gian sống, và lối thoát duy nhất là thuộc địa hóa các thế giới khác. Đã đến lúc khám phá những hệ sao mới.”
– Stephen Hawking
Chúng ta sẽ đi đâu? Tất nhiên là đến những vì sao mới! Vì xét theo quy mô thiên hà, thì ngôi sao gần nhất chỉ cách chúng ta có hơn 4 năm ánh sáng – gần như “với tay là tới”. Đó chính là sao Proxima (từ tiếng Latinh proxima – “gần nhất”), thuộc hệ sao Alpha Centauri. Theo các nhà thiên văn học, xung quanh ngôi sao này có một hành tinh khá lý tưởng để sinh sống, với khối lượng xấp xỉ 1.3 lần khối lượng Trái Đất.
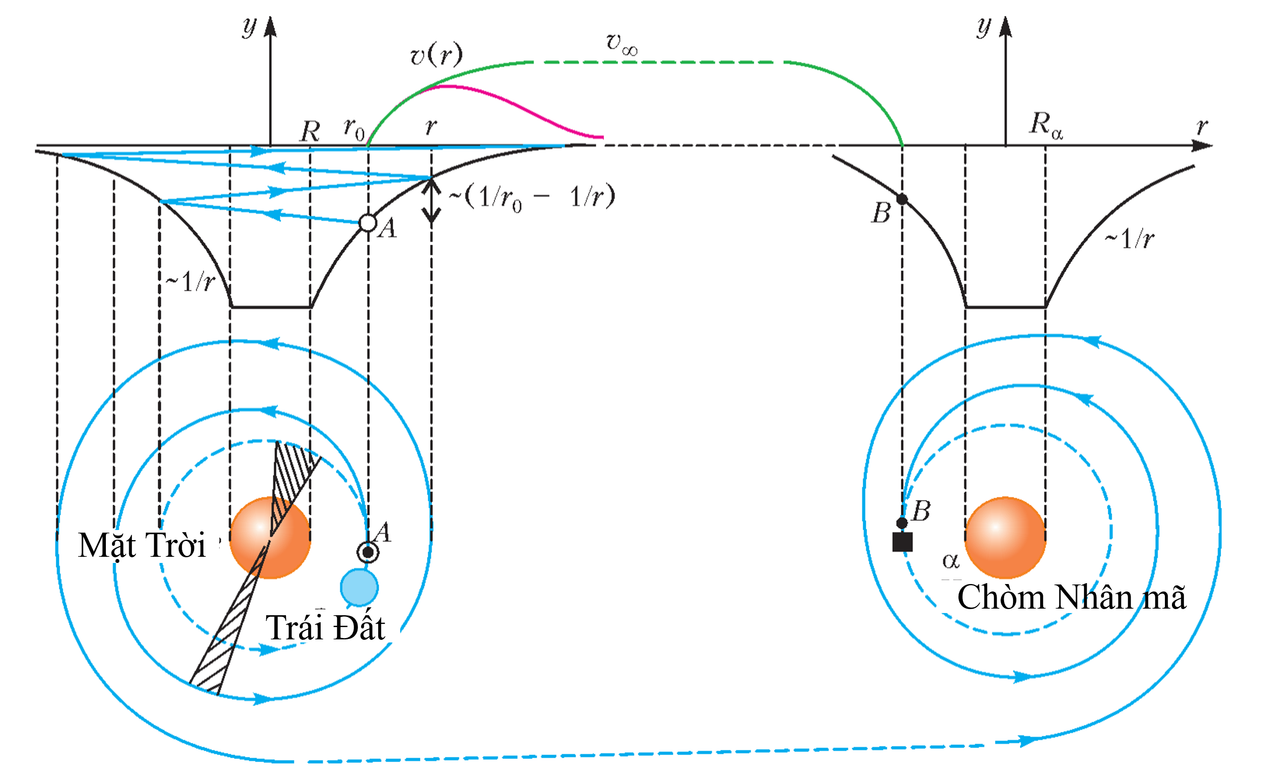
Nhưng trước tiên, cần vượt qua lực hấp dẫn của chính Mặt Trời – nói cách khác, thoát khỏi cái “giếng thế năng” của nó (xem hình minh họa). Và ở đây, chính Mặt Trời có thể giúp ta: thông qua các dòng hạt và photon phát ra – tức gió Mặt Trời và ánh sáng mặt trời.
Ý tưởng rằng ánh sáng có thể tạo áp lực lên vật thể đã được Johannes Kepler đề xuất từ năm 1604, khi ông giải thích tại sao đuôi sao chổi luôn hướng ngược lại Mặt Trời. Đến năm 1873, James Clerk Maxwell chứng minh hiện tượng này bằng lý thuyết điện từ. Năm 1899, nhà vật lý người Nga Pyotr Lebedev đã xác nhận bằng thực nghiệm sự tồn tại của áp suất ánh sáng. Kết quả ấy buộc Lord Kelvin (William Thomson), người từng phản đối Maxwell, phải thừa nhận mình đã sai.
Năm 1924, kỹ sư F. A. Tsander lần đầu tiên đề xuất ý tưởng dùng “cánh buồm ánh sáng” để bay đến sao Hỏa. Gần đây, cả các nhà vật lý lý thuyết lẫn các tỷ phú công nghệ đều đã đưa ra những dự án cụ thể cho tàu liên sao dùng buồm ánh sáng. Dự án khiêm tốn nhất dự kiến đưa một tải trọng nano đến hệ Alpha Centauri bằng buồm có diện tích chỉ $16\,\mathrm{m}^2$. Còn dự án lớn nhất thì dùng buồm khổng lồ diện tích lên đến $10^5\,\mathrm{m}^2$ – tương đương hơn chục sân bóng đá!
Chiếc tàu buồm ánh sáng ấy sẽ cần 100 năm để đạt tới tốc độ tối đa (từ $0{,}05c$ đến $0{,}1c$ – tức 5–10% tốc độ ánh sáng), sau đó mất 50 năm để hãm tốc khi đến gần ngôi sao mục tiêu. Quá trình trở về cũng mất chừng ấy thời gian – tổng cộng khoảng 300 năm cho toàn bộ chuyến đi. NASA, với cái nhìn thực tế, hy vọng dự án như vậy có thể bắt đầu vào năm 2069.
Vậy tại sao lại chọn buồm ánh sáng? Bởi vì đây là loại lực đẩy “miễn phí”, không cần nhiên liệu hay thiết bị phức tạp. Tất nhiên, không thể dùng nó để phóng tàu từ Trái Đất – cần một tên lửa mạnh đưa tàu vào quỹ đạo trước khi bung buồm ánh sáng.
Giả sử một tàu vũ trụ đang chuyển động quanh Mặt Trời theo một quỹ đạo tròn bán kính $r_0$, và nó đã bung ra một cánh buồm có diện tích $S$, hướng vuông góc với các tia sáng Mặt Trời.
Theo định luật thứ hai của Kepler trong cơ học thiên thể, mô men động lượng của một vật thể trong trường hấp dẫn – hay chính là diện tích được bán kính-vectơ của vật quét trong những khoảng thời gian bằng nhau – là đại lượng không đổi (xem hai khu vực gạch chéo trên hình minh họa). Điều này có nghĩa là ở mọi điểm trên quỹ đạo của cánh buồm, ta có:
$$ur = u_0 r_0$$
trong đó $u$ là thành phần vận tốc tiếp tuyến (hay vận tốc tuyến tính). Nhắc lại, vectơ vận tốc gồm có hai thành phần: $u$ – tiếp tuyến và $v$ – hướng tâm.
Kể từ lúc cánh buồm bung ra, năng lượng động học của tàu sẽ tăng dần do tác động của áp lực ánh sáng từ Mặt Trời. Hãy tính công của lực này.
Mỗi photon có tần số $v$ sẽ mang một động lượng bằng:
$$\frac{hv}{c}$$
trong đó $h$ là hằng số Planck, $c$ là tốc độ ánh sáng.
Do đó, nếu mật độ năng lượng tại điểm cách Mặt Trời một khoảng $r$ là $q(r)$ (đơn vị J/($m^2 \cdot c$)), thì áp lực ánh sáng sẽ là:
$$\frac{q(r)}{c}$$
Nếu toàn bộ photon phản xạ lại theo kiểu gương từ diện tích $S$, thì lực tác dụng là:
$$\frac{2q(r)S}{c}$$
Giả sử tại quỹ đạo tròn ban đầu (quỹ đạo Trái Đất) bán kính $r_0$, mật độ năng lượng là $q_0$, thì ở khoảng cách $r$ ta có:
$$q(r) = q_0 \left( \frac{r_0}{r} \right)^2$$
Lưu ý rằng sự phụ thuộc theo $1/r^2$ này cũng giống với lực hấp dẫn tác dụng lên một đơn vị khối lượng:
$$\frac{F}{m} = -\frac{GM}{r^2} = -\frac{GM}{r_0^2} \left( \frac{r_0}{r} \right)^2$$
trong đó $M$ là khối lượng của ngôi sao (Mặt Trời), $G$ là hằng số hấp dẫn.
Công của lực hấp dẫn khi chuyển từ điểm $r_0$ đến $r$ chính là hiệu thế năng, tức là:
$$GM\left(\frac{1}{r_0} - \frac{1}{r}\right) = \frac{GM}{r_0}\left(1 - \frac{r_0}{r}\right)$$
Tương tự, công của áp lực ánh sáng sẽ là:
$$\frac{2q_0 r_0 S}{c m} \left(1 - \frac{r_0}{r} \right)$$
Bây giờ, ta có thể phát biểu một điều quan trọng: sự thay đổi tổng năng lượng (thế và động năng) trên mỗi đơn vị khối lượng bằng công của lực ánh sáng khi tàu di chuyển từ $r_0$ đến $r$:
\begin{align} \frac{u^2}{2} + \frac{v^2}{2} - \frac{u_0^2}{2} - \frac{v_0^2}{2} + \frac{GM}{r_0} \left(1 - \frac{r_0}{r} \right) \approx\\ \approx\frac{2q_0 r_0 S}{c m} \left(1 - \frac{r_0}{r} \right) \end{align}
Sử dụng mối liên hệ giữa các vận tốc tiếp tuyến, ta viết lại động năng thành phần tiếp tuyến:
$$\frac{u^2}{2} = \frac{u_0^2}{2} \left( \frac{r_0}{r} \right)^2$$
Còn tốc độ ban đầu $u_0$ trên quỹ đạo tròn quanh Mặt Trời tìm được từ định luật II Newton:
$$\frac{u_0^2}{r_0} = \frac{GM}{r_0^2}$$
Kết quả, ta thu được biểu thức cho thành phần vận tốc hướng tâm:
$$ v^2 - v_0^2 = -\frac{GM}{r_0} \left(1 - \frac{r_0}{r} \right)^2 + \frac{Q}{\pi c r_0} \cdot \frac{S}{m} \left(1 - \frac{r_0}{r} \right) $$
Ở đây, ta đã đưa vào công suất bức xạ của ngôi sao: $Q = 4\pi r_0^2 q_0$.
Ta thấy rằng, nếu $r/r_0 \rightarrow \infty$, tức là tàu bay ra rất xa khỏi ngôi sao, thì biểu thức trên cho ta vận tốc cuối cùng mà tàu có thể đạt được nhờ cánh buồm ánh sáng:
$$ v_\infty^2 = v_0^2 - \frac{GM}{r_0} + \frac{Q}{\pi c r_0} \cdot \frac{S}{m} $$
Giả thiết rằng mặt phẳng quỹ đạo tròn ban đầu chứa đường thẳng nối tâm của Mặt Trời và ngôi sao đích.
Giả sử ban đầu tàu không có vận tốc hướng tâm, tức $v_0 = 0$ – nghĩa là nó chuyển động tròn đều và không có lực nào đẩy nó theo phương hướng tâm, ngoại trừ lực do buồm ánh sáng tạo ra. Khi đó, từ biểu thức trên, ta rút ra được một kết quả thú vị: giới hạn trên của mật độ khối lượng bề mặt của buồm – tức tỉ số $m/S$ – để buồm có thể giúp tàu **vừa đủ thoát khỏi giếng thế năng** (với $v_\infty = 0$):
$$ \left( \frac{m}{S} \right)_{\text{max}} = \frac{Q}{M} \cdot \frac{1}{\pi c G} $$
Biểu thức này bao gồm hai hằng số cơ bản: $c$ – tốc độ ánh sáng, $G$ – hằng số hấp dẫn; và đặc trưng duy nhất của ngôi sao – suất phát xạ riêng $Q/M$ (đơn vị là W/kg). Và tất nhiên không thể thiếu hằng số quen thuộc $\pi$, bởi vì cả ngôi sao lẫn quỹ đạo đều "tròn".
Nếu xét với các sao giống Mặt Trời, thì $Q \sim M^4$, biểu thức trên có thể đơn giản hơn:
$$ \left( \frac{m}{S} \right)_{\text{max}} \sim M^3 $$
Đến đây, hãy thử ước lượng bằng số. Theo dữ liệu bảng tra:
- Khối lượng Mặt Trời: $M = 2 \cdot 10^{30}$ kg
- Khoảng cách từ Mặt Trời đến Trái Đất: $r_0 = 150$ triệu km
- Mật độ dòng bức xạ tại quỹ đạo Trái Đất: $q_0 = 1400\,\mathrm{W/m^2}$
- Hằng số hấp dẫn: $G = 6{,}67 \cdot 10^{-11}\,\mathrm{N \cdot m^2/kg^2}$
- Tốc độ ánh sáng: $c = 3 \cdot 10^8\,\mathrm{m/s}$
Thay số vào công thức, ta được:
$$ \left( \frac{m}{S} \right)_{\text{max}} \approx 10^{-3}\,\mathrm{kg/m^2} $$
Vậy nếu buồm ánh sáng nặng hơn giá trị này, nó sẽ không thể "thoát" khỏi phạm vi ảnh hưởng của Mặt Trời. Nhưng buồm ấy còn phải mang theo cả tải trọng hữu ích, không chỉ chính nó. Vì thế, người ta đề xuất tăng cường lực đẩy bằng cách chiếu tia laser từ Trái Đất vào buồm. Khi tàu bay xa hơn, người ta có thể dùng các gương được bố trí sẵn dọc đường để phản xạ ánh sáng Mặt Trời, tiếp tục "thắp sáng" cho buồm khi nó lướt qua không gian liên sao.
Và rồi – như trong mọi dự án vĩ đại – xuất hiện thêm nhiều yếu tố cần cân nhắc. Ngoài bức xạ điện từ đã xét ở trên, còn tồn tại cả **bức xạ hạt** của Mặt Trời: một dòng proton bay với tốc độ khoảng $450\,\mathrm{km/s}$, gây nên áp suất khoảng $p_0 \sim 2 \cdot 10^{-7} \cdot \left( \frac{r_0}{r} \right)^2$.
Đáng chú ý, khi Mặt Trời hoạt động mạnh (chu kỳ bùng nổ), cường độ của bức xạ hạt này có thể tăng lên **gấp hàng trăm đến hàng nghìn lần**. Dĩ nhiên, các hạt này cũng góp phần tạo lực đẩy cho buồm ánh sáng. Nhưng điều đáng lo là: chúng sẽ tương tác với lớp màng mỏng của buồm như thế nào? Liệu chúng có biến buồm thành một tấm lưới thủng lỗ chỗ, rồi thành mạng nhện, và cuối cùng là... bụi vũ trụ?
Một vấn đề nữa là: mục tiêu bay của ta không nằm trong mặt phẳng hoàng đạo (mặt phẳng quỹ đạo Trái Đất quanh Mặt Trời), nên sẽ cần thêm các **manipulation quỹ đạo** phức tạp.
Và nếu Galileo còn sống, chắc hẳn ông sẽ thêm một “chỉnh lý” quan trọng: nếu ánh sáng truyền với tốc độ $c$ và va vào một buồm đang di chuyển hướng tâm với tốc độ $v$, thì vận tốc tương đối giữa ánh sáng và buồm phải nhỏ hơn $c$. Tuy nhiên, vật lý hiện đại khẳng định rằng **vận tốc ánh sáng luôn bằng $c$ trong mọi hệ quy chiếu**.
Vậy thì điều gì sẽ thay đổi so với trường hợp buồm chuyển động trên quỹ đạo tròn? Có thể là **tần số của photon sẽ thay đổi** – tức là năng lượng và động lượng của nó thay đổi – photon sẽ “đỏ hóa” khi đi xa khỏi nguồn hấp dẫn phát ra nó?
Còn thi sĩ thì sao?... Với họ, Proxima gần đó chẳng là gì:
“Sống mãi niềm đam mê cháy bỏng,
Tổ tiên truyền lại tự bao đời.
Kìa sương mù Andromeda vẫy gọi,
Giữa câm lặng vũ trụ rợp ngàn khơi.”
Thế nhưng thiên hà Andromeda cách chúng ta tới **1,5 triệu năm ánh sáng**! Với những vận tốc dưới ánh sáng hiện tại, quả là quá xa xôi: ánh sáng từ Andromeda mà ta thấy hôm nay đã rời khỏi đó từ khi **loài người còn chưa xuất hiện trên Trái Đất**.
Song, vẫn còn le lói một tia hy vọng: các nhà vật lý thiên văn đã phát hiện ra trong không gian những **“hố sâu” (wormholes)** – những đường hầm vũ trụ có thể đưa ta đi “tắt” qua các vùng xa xôi của vũ trụ...
Bạn có thể ủng hộ các bài viết của DẠY HỌC SÁNG TẠO bằng việc nhấp vào quảng cáo trên trang, biết đâu bạn sẽ tìm cho mình được một sản phẩm phù hợp với nhu cầu của bạn.


0 nhận xét:
Đăng nhận xét