
Tác giả: S. Kozel
“Có gì mà nghịch lý ở đây chứ?” — độc giả có thể thốt lên — “Đây là một hệ thống điện đơn giản đến mức ai cũng hiểu mà.” Và đúng vậy, có gì đơn giản hơn một tụ điện phẳng? Từ sách giáo khoa vật lý phổ thông, chúng ta biết rằng đây là một hệ thống gồm hai bản dẫn điện đặt song song cách nhau một khoảng nhỏ, ở giữa có một lớp điện môi.
Nếu hai bản (hay gọi là hai bản cực) của tụ điện được nối với hai cực của một nguồn điện, thì trên một bản sẽ tích điện dương $+q$, và bản còn lại tích điện âm $-q$. Trường điện của tụ điện phẳng chủ yếu tập trung trong không gian giữa hai bản. Trường này là đồng đều, nghĩa là véc-tơ cường độ điện trường giống nhau tại mọi điểm trong vùng đó.
Điện dung của tụ điện phẳng được biểu diễn bởi công thức:
$$ C = \frac{q}{\Delta\varphi} = \frac{\varepsilon_0 \varepsilon S}{d} $$
trong đó $\Delta\varphi$ là hiệu điện thế giữa hai bản tụ, $S$ là diện tích mỗi bản, $d$ là khoảng cách giữa chúng, $\varepsilon$ là hằng số điện môi của môi trường, còn $\varepsilon_0$ là hằng số điện.
Có vẻ như mọi thứ đã rất rõ ràng. Tuy nhiên, nhiều thí sinh khi gặp bài toán liên quan đến tụ điện phẳng trong kỳ thi lại cảm thấy bối rối. Trong một số trường hợp, dù dựa vào những kiến thức tưởng như quen thuộc, họ lại đưa ra kết quả mâu thuẫn nhau, dẫn đến những tình huống nghịch lý.
Tất nhiên, tất cả những nghịch lý này đều có thể giải thích được, nếu ta chịu khó đi sâu và nhìn nhận các định luật của điện học một cách không máy móc. Dưới đây là một số ví dụ.
Đăng trên tạp chí "Kvant", số 8 năm 1985
Nghịch lý 1
Hãy xét một tụ điện phẳng có môi trường là không khí đã được tích điện. Hiệu điện thế giữa hai bản là:
$$ \Delta\varphi = \frac{q}{C} = \frac{qd}{\varepsilon_0 S} $$
Lưu ý rằng $\Delta\varphi$ tỉ lệ thuận với khoảng cách $d$ giữa hai bản tụ. Điều này có nghĩa là: nếu ta kéo giãn khoảng cách giữa hai bản tụ đã tích điện, thì hiệu điện thế giữa chúng sẽ tăng lên.
Ví dụ, nếu ta tích điện cho tụ sao cho ban đầu hiệu điện thế là 10 V, rồi tăng khoảng cách $d$ lên gấp $10^3$, $10^4$, ... lần, thì $\Delta\varphi$ sẽ đạt tới $10^4\ \text{V}$, $10^5\ \text{V}$, v.v. Một cách đơn giản và hiệu quả để tạo ra máy gia tốc hạt mang điện! Nghe thật hấp dẫn, phải không?
Tuy nhiên, rõ ràng là chúng ta đang mâu thuẫn với trực giác vật lý — một bước nữa thôi là vi phạm định luật bảo toàn năng lượng.
Vậy, lập luận của chúng ta có đúng không? Thông thường, thí sinh sẽ phản ứng ngay rằng điều đó không thể xảy ra. Nhưng không phải ai cũng chỉ ra được nguyên nhân vật lý cụ thể của vấn đề này.
Thật ra, câu trả lời rất đơn giản. Công thức điện dung của tụ điện phẳng chỉ đúng khi khoảng cách $d$ đủ nhỏ, tức là khi $d$ nhỏ hơn rất nhiều so với kích thước của bản tụ. Khi $d$ quá lớn, điện trường giữa các bản không còn đồng đều nữa, và hiệu điện thế $\Delta\varphi$ không còn tỉ lệ tuyến tính với $d$.
Điều này dẫn ta đến một khía cạnh rất quan trọng: giới hạn áp dụng của các kết quả vật lý. Mỗi mô hình vật lý chỉ có hiệu lực trong một phạm vi nhất định. Ví dụ, ta không thể áp dụng mô hình khí lý tưởng cho khí thực ở áp suất cao hoặc nhiệt độ thấp. Tương tự, công thức điện dung của tụ phẳng sẽ "mất tác dụng" khi khoảng cách giữa các bản quá lớn và trường điện không còn đồng đều.
Không thể áp dụng trực tiếp định luật Coulomb để tính lực tương tác điện giữa hai bản của tụ điện phẳng trong trường hợp này. Đáng tiếc, nhiều thí sinh vẫn mắc sai lầm khi làm điều đó.
Trong khi nhiều thí sinh nhầm lẫn và viết:
$$ F = \frac{q^2}{4\pi\varepsilon_0 d^2} $$
thì công thức đúng cho lực tương tác giữa các bản của tụ điện phẳng là:
$$ F = q \cdot \frac{E}{2} = \frac{q^2}{2\varepsilon_0 S} $$
(ở đây lực không phụ thuộc vào khoảng cách $d$).
Bài toán 1
Hãy thử ước lượng xem có thể tăng hiệu điện thế giữa các bản của tụ điện phẳng đã tích điện lên bao nhiêu lần nếu kéo các bản ra rất xa nhau. Kích thước mỗi bản được coi là $a = \sqrt{S}$ và khoảng cách ban đầu giữa các bản là $d$ (đều đã biết).
Chú ý rằng những bài toán ước lượng như thế này, nơi việc tính toán chính xác gặp khó khăn, lại có vai trò rất quan trọng trong vật lý. Chúng đòi hỏi phải chọn mô hình vật lý đơn giản hóa và cho phép đánh giá bậc độ lớn của hiện tượng.
Nghịch lý 2
Giả sử ta có một tụ điện phẳng đã được tích điện và cách ly. Ta khoan hai lỗ nhỏ trên hai bản của tụ — lỗ này đối diện với lỗ kia. Khi đó, trường điện trong tụ gần như không thay đổi và vẫn đồng đều. Giả sử có một hạt mang điện bay vào tụ thông qua một lỗ với vận tốc ban đầu nhỏ, sao cho điện trường trong tụ làm tăng tốc hạt đó (hình 1). (Hiển nhiên là hạt phải đi vào từ phía bản có điện tích cùng dấu với hạt để chịu lực đẩy).
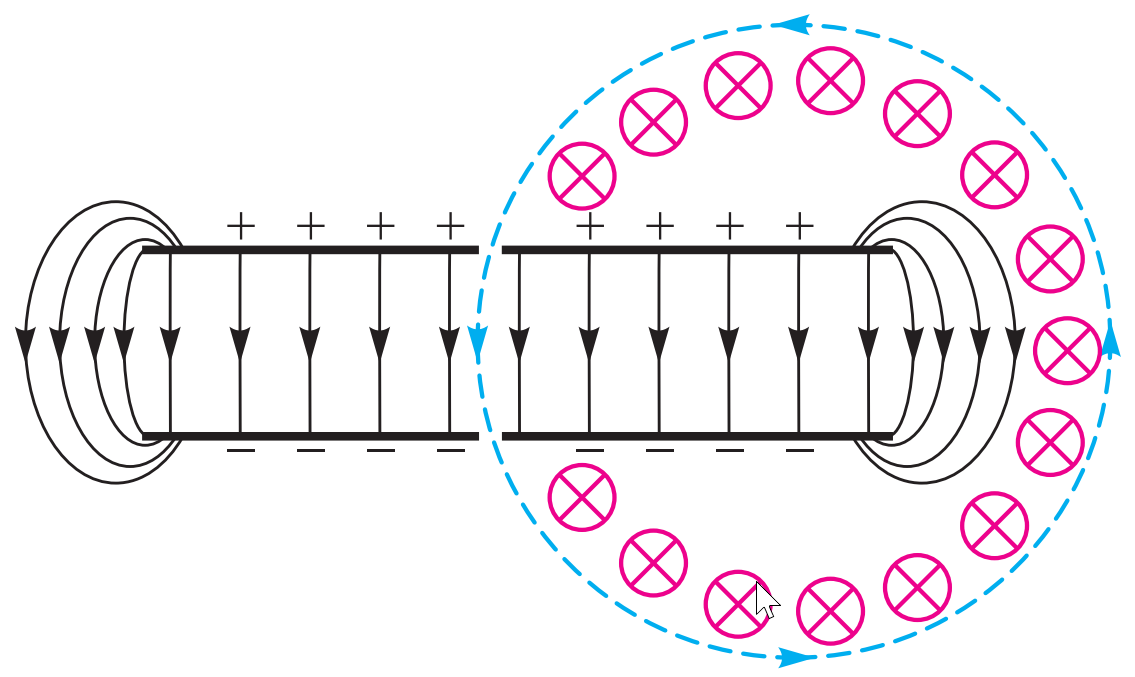
Sau khi đi qua tụ, hạt bay ra khỏi lỗ phía đối diện, và nhận thêm một năng lượng:
$$ \Delta W = q \Delta\varphi $$
Bây giờ ta dùng một từ trường để bẻ hướng chuyển động của hạt sao cho nó lại bay trở lại qua lỗ đầu tiên để đi vào tụ một lần nữa. Nhắc lại rằng lực Lorentz do từ trường tác dụng lên hạt chuyển động không sinh công, vì nó vuông góc với vận tốc của hạt.
Mỗi lần đi qua tụ, hạt lại nhận thêm năng lượng $\Delta W$, và nếu lặp lại nhiều lần, ta tưởng chừng đã tạo ra một máy gia tốc tuần hoàn không cần nguồn năng lượng. Thêm một chút tưởng tượng nữa — và ta có thể "chế tạo" ra động cơ vĩnh cửu chạy mãi mãi không cần năng lượng!
Kết luận sai lầm này xuất hiện do ta đã không xét đến một trong những tính chất cơ bản của điện trường tĩnh: tính chất thế năng (tính bảo toàn năng lượng thế).
Tính thế năng của điện trường tĩnh có nghĩa là: nếu ta di chuyển một vật tích điện từ điểm này đến điểm khác, công của lực điện không phụ thuộc vào hình dạng đường đi mà chỉ phụ thuộc vào vị trí đầu và cuối. Do đó, nếu ta di chuyển theo một quỹ đạo khép kín, thì công toàn phần của lực điện bằng không. (Tính chất tương tự cũng đúng với trường hấp dẫn).
Trong ví dụ của chúng ta, khi hạt mang điện bay qua bên trong tụ, nó được gia tốc. Nhưng khi bay bên ngoài tụ (từ lỗ thoát đến lỗ vào), nó sẽ bị giảm tốc bởi điện trường yếu bên ngoài. Khi quay lại vị trí ban đầu, hạt đã mất đúng bằng năng lượng nó đã nhận được bên trong tụ. Điều này chứng tỏ rằng ta không thể bỏ qua điện trường bên ngoài của tụ điện phẳng. Dù nó yếu hơn rất nhiều so với trường bên trong, nhưng hạt lại chuyển động trong vùng đó trên quãng đường dài hơn, và tổng công của lực điện bên ngoài cân bằng năng lượng tăng bên trong.
Nghịch lý 3
Chúng ta tiếp tục với một ví dụ khác, chứng minh rằng việc bỏ qua điện trường bên ngoài tụ điện phẳng (hay còn gọi là trường rò ngoài) có thể dẫn đến sai lầm nghiêm trọng...
Bỏ qua trường rò bên ngoài (trường phân tán) có thể dẫn đến những kết luận sai lầm về bản chất.
Trong sách giáo khoa phổ thông có nêu rằng: các vật thể, kể cả vật dẫn, được đặt bên ngoài tụ điện phẳng thì hầu như không ảnh hưởng đến điện dung của nó. Phần lớn các trường hợp điều này đúng.
Giả sử gần một bản của tụ điện phẳng có đặt một bản dẫn khác, không tích điện — gọi là bản a (xem hình 2). Bản này không làm thay đổi điện trường bên trong tụ, và điện dung vẫn giữ nguyên. Bây giờ ta đặt thêm một bản dẫn khác — bản b, gần bản tụ còn lại. Bản này cũng không ảnh hưởng đến điện dung tụ.
Nhưng nếu bây giờ ta nối hai bản ngoài (a và b) với nhau bằng dây dẫn thì sao? Khi đó, tụ điện của chúng ta như thể được đặt trong một “hộp kim loại dẫn điện”. Điều gì sẽ xảy ra?
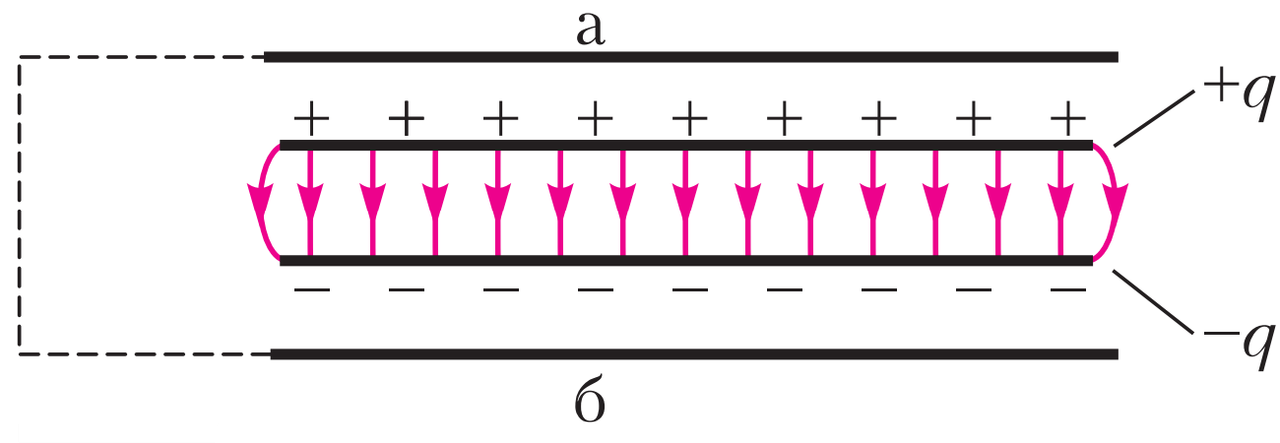
Nhiều thí sinh cho rằng: do các bản ngoài không tích điện, nên trường giữa hai bản tụ không đổi, và điện dung không thay đổi. Nhưng điều đó là sai lầm.
Sơ đồ ở hình 2 (sau khi nối hai bản ngoài lại) tương đương với một mạch gồm ba tụ điện mắc nối tiếp (xem hình 3). Nếu các khoảng cách giữa các bản là như nhau, thì điện dung tổng cộng của hệ này là:
$$ C = \frac{3}{2}C_0 $$
trong đó $C_0$ là điện dung ban đầu của tụ điện.
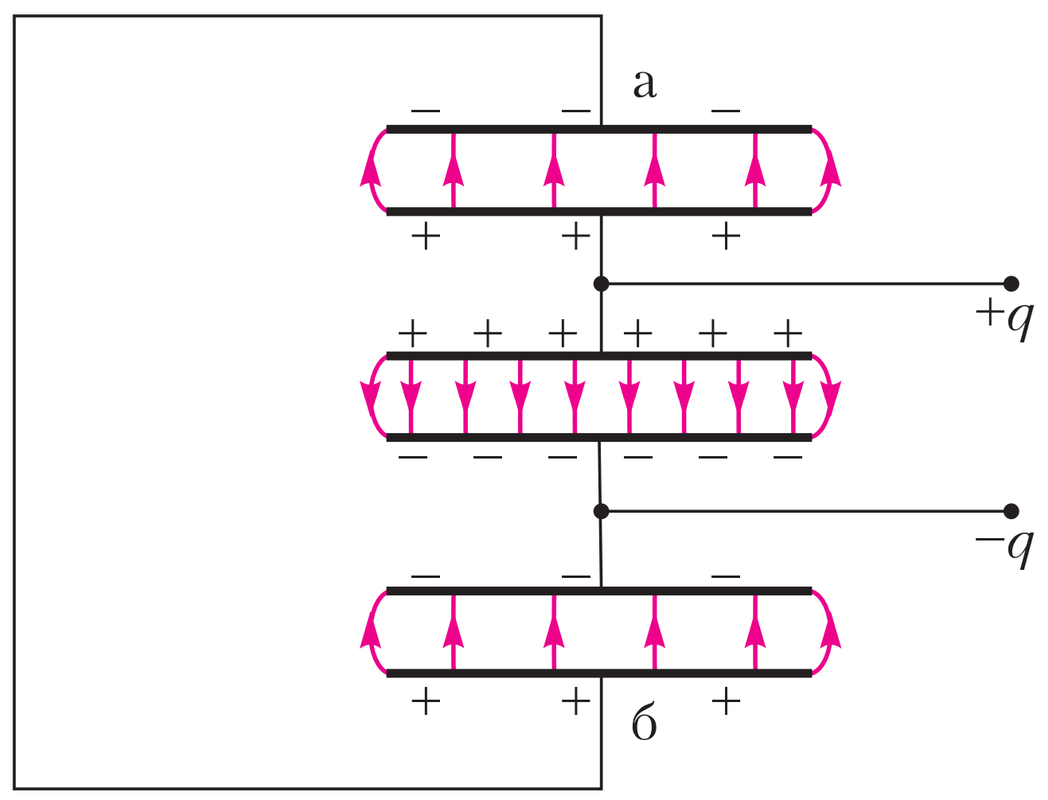
Vậy là điện dung đã thay đổi — tăng lên gấp 1,5 lần! Làm sao có thể giải thích điều này?
Nguyên nhân nằm ở trường rò của tụ điện. Dưới tác dụng của trường này, điện tích trên các bản ngoài sẽ bị phân bố lại: bản a trở nên mang điện âm, bản b mang điện dương. (Thú vị là, từ hình 3 ta thấy: nếu nối một trong hai bản ngoài với một trong các bản chính của tụ, thì điện dung sẽ là $2C_0$.)
Nghịch lý 4
Giả sử ta có hai tụ điện giống hệt nhau (không nhất thiết là tụ phẳng), mỗi tụ có điện dung $C$. Một tụ đã được nạp điện với điện tích $q_0$, tụ còn lại thì chưa có điện tích.
Lượng năng lượng điện được tích trữ ban đầu là:
$$ W_1 = \frac{q_0^2}{2C} + 0 $$
Bây giờ, ta nối hai tụ điện lại song song với nhau. Khi đó, tổng điện tích trong hệ vẫn là $q_0$, còn điện dung tổng cộng là $2C$. Lúc này, năng lượng điện của hệ là:
$$ W_2 = \frac{q_0^2}{2(2C)} = \frac{1}{2}W_1 $$
Vậy một nửa năng lượng ban đầu đã “biến mất” đi đâu? (Lưu ý rằng khi nối hai tụ điện lại, ta không thực hiện công nào từ bên ngoài cả.)
Để hiểu rõ hơn, ta xét trường hợp nối hai tụ điện qua một điện trở có điện trở $R$ (xem hình 4). Khi các tụ điện “chia lại” điện tích, sẽ có dòng điện chạy qua điện trở, và do đó sinh ra nhiệt lượng Joule. Mọi thứ có vẻ đã rõ.
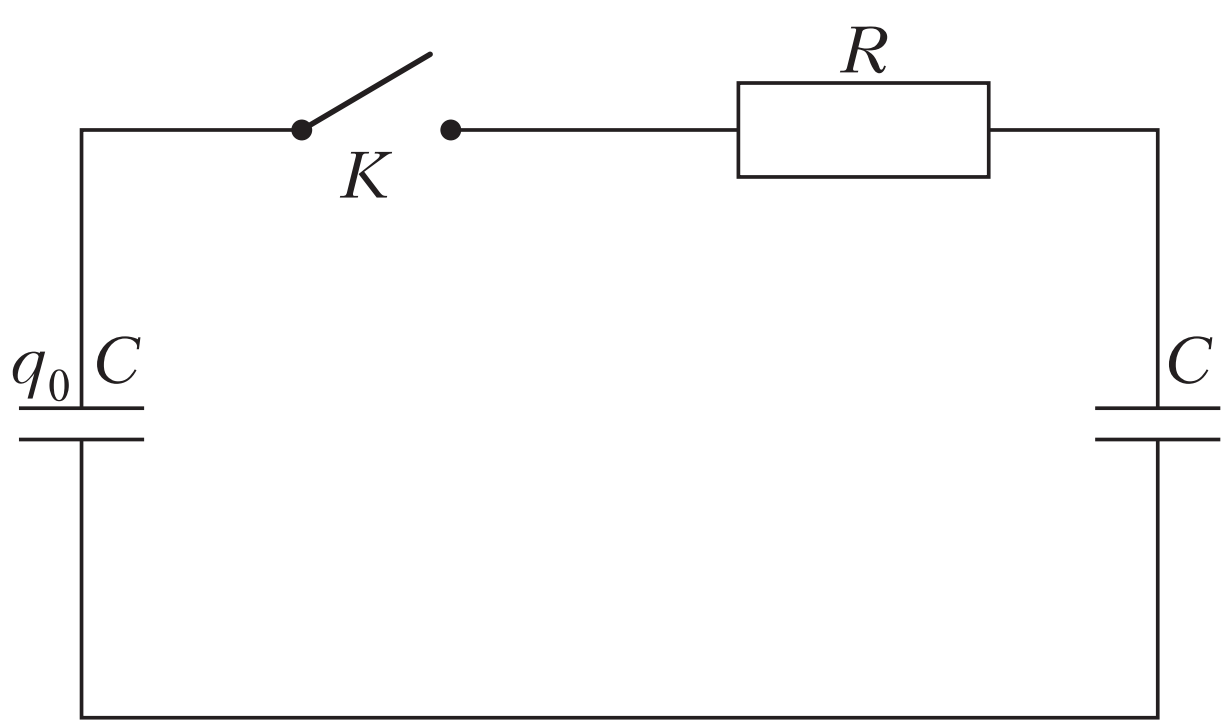
Nhưng liệu ta có thể kiểm chứng điều đó bằng tính toán không? Hãy thực hiện phép tính. Đầu tiên, cần xác định sự phụ thuộc của dòng điện theo thời gian.
Gọi $q(t)$ là điện tích trên tụ bên phải tại thời điểm $t$...
Sau khi đóng công tắc, giả sử điện tích trên tụ bên phải là $q$. Khi đó, điện tích trên tụ bên trái sẽ là $q_0 - q$. Dòng điện qua điện trở $R$ là:
$$ i = \frac{1}{R} \left( \frac{q_0 - q}{C} - \frac{q}{C} \right) = \frac{1}{RC}(q_0 - 2q) $$
Vì dòng điện là đạo hàm của điện tích theo thời gian ($i = \frac{dq}{dt}$), ta thu được phương trình vi phân:
$$ \frac{dq}{dt} + \frac{2}{RC}q = \frac{1}{RC}q_0 $$
Để thuận tiện, ta chuyển sang viết phương trình theo biến $i$ bằng cách vi phân hai vế theo thời gian:
$$ \frac{di}{dt} + \frac{2}{RC}i = 0 \quad \text{hay} \quad di = -\frac{2}{RC}i \, dt $$
Phương trình này dễ dàng tích phân được. Tích phân hai vế từ $i_0$ đến $i(t)$ và từ $0$ đến $t$:
$$ \ln i(t) - \ln i_0 = -\frac{2}{RC}t \quad \Rightarrow \quad i(t) = i_0 e^{-2t/(RC)} $$
Giá trị ban đầu $i_0$ có thể xác định như sau: ban đầu, tụ trái có hiệu điện thế $\frac{q_0}{C}$, còn tụ phải chưa tích điện. Toàn bộ hiệu điện thế rơi trên điện trở, nên:
$$ i_0 = \frac{q_0}{CR} $$
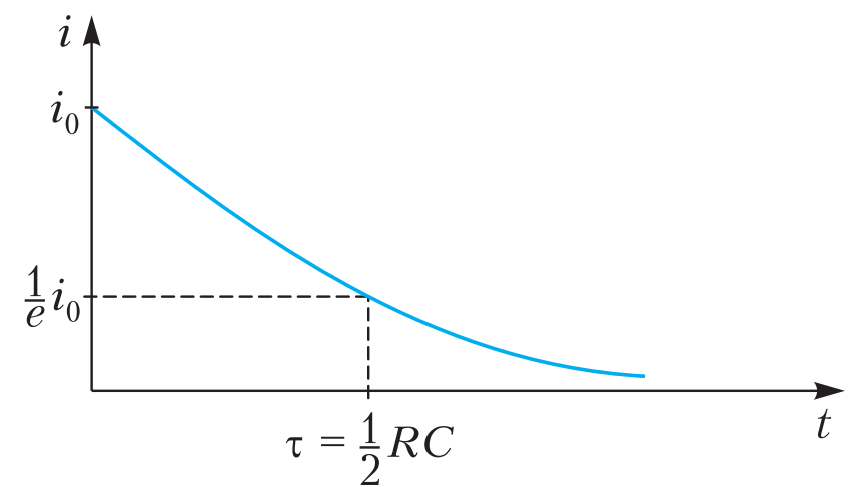
Hàm số $i(t)$ là một hàm mũ giảm. Các hàm như vậy rất thường gặp trong vật lý. Thời gian $\tau$, trong đó dòng điện giảm đi $e$ lần, được gọi là hằng số thời gian:
$$ \tau = \frac{CR}{2} $$
R rõ ràng, càng nhỏ thì dòng điện tắt càng nhanh.
Bây giờ ta tính nhiệt lượng tỏa ra trên điện trở (nhiệt Joule):
\[ \begin{aligned} Q &= \int_0^\infty i^2(t)R\,dt = \frac{q_0^2}{C^2R} \int_0^\infty e^{-4t/(RC)}dt \\ &= \frac{q_0^2}{C^2R} \cdot \left( \frac{RC}{4} \right) = \frac{q_0^2}{4C} = \frac{1}{2}W_1 \end{aligned} \]
Vậy là nghịch lý đã được giải quyết: bất kể giá trị của $R$, một nửa năng lượng ban đầu của tụ điện được chuyển thành nhiệt, và nửa còn lại vẫn được lưu giữ dưới dạng năng lượng điện của hai tụ sau khi phân bố lại điện tích.
Vậy điều gì xảy ra khi $R \to 0$? Nếu ta nối tụ bằng dây dẫn lý tưởng (siêu dẫn), thì không còn tổn hao nhiệt. Công thức trên vẫn đúng, nhưng năng lượng bị “mất” dưới dạng nào?
Trong trường hợp lý tưởng đó, năng lượng không chuyển thành nhiệt, mà thành bức xạ điện từ. Khi dòng điện thay đổi nhanh trong mạch, sẽ sinh ra sóng điện từ mang đi một phần năng lượng.
Đồng thời, cần xét đến độ tự cảm nhỏ của dây nối. Khi đó, mạch trở thành một mạch dao động với độ tắt dần nhỏ. Quá trình nạp lại điện cho các tụ trở thành dao động, và không thể bỏ qua bức xạ điện từ vào không gian.
Bài toán 2 (tự giải)
Giả sử có một tụ điện chưa tích điện với điện dung $C$ và một nguồn điện có suất điện động $\varepsilon$. Khi nối hai bản tụ vào hai cực của nguồn, trên tụ xuất hiện điện tích:
$$ q = C\varepsilon $$
Tụ điện sẽ tích trữ một năng lượng:
$$ W = \frac{1}{2}C\varepsilon^2 $$
Trong khi đó, công mà nguồn điện thực hiện là:
$$ A = q\varepsilon = C\varepsilon^2 $$
Rõ ràng, $W = \frac{1}{2}A$. Câu hỏi đặt ra: nửa còn lại của công nguồn điện đã “đi đâu”?
Nghịch lý 5
Một tụ điện phẳng có điện dung $C$ được đổ đầy chất lỏng điện môi với hằng số điện môi $\varepsilon$, rồi được nạp điện đến hiệu điện thế $U$. Khi đó, tụ điện tích trữ năng lượng:
$$ W_1 = \frac{1}{2} \varepsilon C U^2 $$
Sau đó, tụ được ngắt khỏi nguồn điện, chất điện môi được rút ra, rồi tụ được xả điện. Khi ấy, điện tích trên tụ không thay đổi ($q = \varepsilon C U$), nhưng điện dung giảm xuống còn $C$. Do đó, năng lượng giải phóng khi xả tụ là:
$$ W_2 = \frac{q^2}{2C} = \frac{(\varepsilon C U)^2}{2C} = \frac{1}{2} \varepsilon^2 C U^2 = \varepsilon W_1 $$
Điều này có nghĩa là: năng lượng thu được khi xả tụ nhiều hơn năng lượng đã nạp vào. Ví dụ, nếu $\varepsilon = 2$, thì $W_2 = 2W_1$ — một kết quả rất nghịch lý.
Dù bài toán này rất phổ biến trong các đề thi, nhiều thí sinh vẫn bối rối. Trong khi đó, lời giải thích lại rất đơn giản: khi rút chất điện môi ra khỏi tụ đang tích điện, cần phải thực hiện một công cơ học dương từ bên ngoài, bởi vì chất điện môi luôn bị hút vào vùng có điện trường mạnh hơn (giữa hai bản tụ).
Chính công của lực ngoài đó làm tăng năng lượng điện của tụ:
$$ W_2 - W_1 = A_{\text{ngoài}} $$
Trong trường hợp của chúng ta, chất điện môi là chất lỏng, và nó chảy ra do tác dụng của trọng lực, nên công của trọng lực làm tăng năng lượng tụ.
Nếu tụ vẫn được nối với nguồn, thì phải tính thêm công của nguồn điện:
$$ W_2 - W_1 = A_{\text{ngoài}} + A_{\text{nguồn}} $$
Biểu thức này chính là định luật bảo toàn năng lượng cho hệ điện tĩnh có ngoại lực tác động.
Bài toán 3 (tự giải)
Hãy xác định:
- Công của lực ngoài
- Công của nguồn điện có suất điện động $\mathcal{E}$
Khi rút chất điện môi có hằng số $\varepsilon$ ra khỏi tụ điện đang được nối với nguồn. Giả sử điện dung ban đầu của tụ (không có điện môi) là $C$.
Nếu trong hệ có điện trở thuần, cần xét cả tổn hao nhiệt. Khi đó, định luật bảo toàn năng lượng được viết dưới dạng:
$$ A_{\text{nguồn}} - Q = \Delta W - A_{\text{ngoài}} $$
Tức là: phần công của nguồn không bị tổn hao dưới dạng nhiệt sẽ dùng để tăng năng lượng điện của hệ và thực hiện công chống lại lực ngoài.
Một số bài toán thêm
Bài toán 4. Một tụ điện phẳng có diện tích mỗi bản là $S$, khoảng cách giữa các bản là $d$. Giữa hai bản người ta đặt một bản kim loại mỏng, không tích điện, có độ dày $l$ và song song với các bản tụ. Tụ nối với nguồn điện có suất $\mathcal{E}$.
Hãy tính công cần thiết để rút bản kim loại ra khỏi tụ điện, trong hai trường hợp:
- a) Trước khi rút, tụ được ngắt khỏi nguồn
- b) Tụ vẫn được nối với nguồn
Bài toán 5. Hai tụ điện phẳng giống hệt nhau, điện dung $C$, đều được nạp điện với điện tích $q$, và đều đã ngắt khỏi nguồn. Sau đó, người ta lồng hai tụ vào nhau theo hai cách như hình 6. Tính công cần thiết trong mỗi trường hợp. Xem bản tụ là mỏng và khoảng cách giữa các bản bằng nhau.
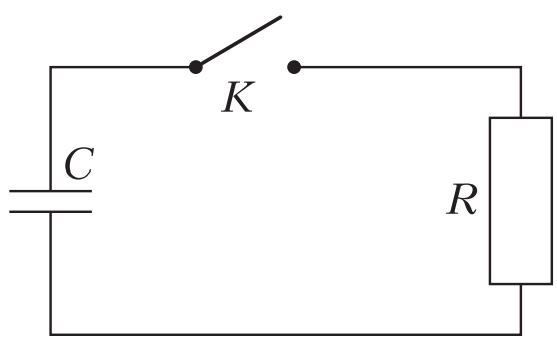
Bài toán 6. Xác định lực tương tác tối đa giữa hai bản của tụ điện phẳng có điện dung $C$, khi tụ được nối vào mạch chứa điện trở $R$, và dòng điện ban đầu cực đại là $i_0$ (xem hình 7). Biết khoảng cách giữa hai bản tụ là $d$.


0 nhận xét:
Đăng nhận xét