Tìm chu kì dao động điều hòa nhỏ bằng phương pháp năng lượng thật là đơn giản

Một trong những nhiệm vụ quan trọng của lý thuyết dao động là xác định chu kỳ của những dao động nhỏ của hệ cơ học quanh vị trí cân bằng. Trong chương trình Vật lý phổ thông, người ta định lượng dao động của những hệ chỉ có một bậc tự do (vị trí được xác định bằng một tham số — độ dịch chuyển, góc lệch, v.v.) và xảy ra không mất mát năng lượng. Ví dụ đơn giản của những hệ như vậy là vật nặng treo trên lò xo và con lắc toán học.

Thông thường, dao động của những hệ như vậy được nghiên cứu bằng phương pháp động lực học. Phương pháp này dựa vào việc đưa phương trình chuyển động của hệ (từ định luật II Newton) về dạng của phương trình dao động điều hòa: $$𝑥''+𝜔^2𝑥=0,\tag{1}$$ trong đó $𝑥''$ là đạo hàm bậc hai của tham số $𝑥$ theo thời gian.

Tuy nhiên, trong một số trường hợp, học sinh phổ thông gặp khó khăn khi lập phương trình dao động. Điều này trước hết xảy ra với các hệ có khối lượng phân bố, hoặc xét một hệ có nhiều vật chuyển động theo nhiều hướng khác nhau. Và khi đó, như thường lệ, định luật bảo toàn năng lượng đến cứu, cho phép mở rộng đáng kể phạm vi các bài toán có thể giải bằng kiến thức phổ thông.

Vậy phương pháp năng lượng trong nghiên cứu dao động là gì? Có thể nói rằng nó dựa trên việc so sánh năng lượng của hệ dao động với năng lượng của hệ đơn giản nhất là con lắc lò xo — một vật khối lượng $𝑚$ gắn với lò xo có độ cứng $𝑘$. Nếu biểu thức năng lượng cơ học của hệ, trong đó độ lệch khỏi vị trí cân bằng được xác định bởi tham số $𝑥$, được đưa về dạng $$𝐸=\frac{1}{2}𝑚_\text{hd}x'^2+\frac{1}{2}k_\text{hd}x^2 \tag{2}\label{2}$$ thì hệ thực hiện dao động điều hòa $$x=A\cos{\left(\omega t+\varphi_0\right)} \tag{3}$$ với tần số góc $$ \omega =\sqrt{\frac{k_\text{hd}}{m_\text{hd}}} \tag{4}$$

Hệ số $m_\text{hd}$ trong biểu thức năng lượng động học được gọi là khối lượng hiệu dụng (thường trùng với khối lượng của hệ), còn hệ số $k_\text{hd}$ trong biểu thức năng lượng thế được gọi là độ cứng hiệu dụng. Thật vậy, do cơ năng lượng được bảo toàn, nên đạo hàm theo thời gian của nó bằng không:

$$ E'(t) = 0 = m_{\text{hd}}\,x'\,x'' + k_{\text{hd}}\,x\,x' \tag{5} $$

và ta thu được phương trình dao động điều hòa:

$$ x'' + \frac{k_{\text{hd}}}{m_{\text{hd}}} x = 0.\tag{6} $$

Ví dụ, để minh họa cách hoạt động của phương pháp năng lượng, ta hãy tìm tần số góc dao động của con lắc đơn có khối lượng quả nặng $m$ và chiều dài dây $l$. Chọn tham số $x$ là độ dịch chuyển của quả nặng theo cung tròn từ vị trí cân bằng. Năng lượng động học của con lắc là \( m x'^2 / 2 \), nghĩa là khối lượng hiệu dụng bằng khối lượng của quả nặng. Thế năng đối với dao động nhỏ \((x \ll l)\) bằng:

$$ E_{\text{t}} = m g h = m g l (1 - \cos\alpha) = 2 m g l \sin^2\frac{\alpha}{2} = m g l \frac{\alpha^2}{2} = \frac{m g}{l} \frac{x^2}{2},\tag{7} $$

trong đó \(\alpha = x / l\) là góc lệch của con lắc. Do đó, độ cứng hiệu dụng bằng \( m g / l \), và tần số góc dao động bằng:

$$ \omega = \sqrt{\frac{k_{\text{hd}}}{m_{\text{hd}}}} = \sqrt{\frac{g}{l}}.\tag{8} $$

Bây giờ, chúng ta tìm chu kì dao động điều hòa bằng phương pháp năng lượng thông qua một số bài toán cụ thể.

MỘT SỐ BÀI TOÁN MẪU ÁP DỤNG PHƯƠNG PHÁP NĂNG LƯỢNG TÌM CHU KÌ DAO ĐỘNG ĐIỀU HÒA

Bài toán 1. Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của hệ lò xo - bánh xe lăn không trượt

Một lò xo có độ cứng $k$ được gắn vào một đầu của trục bánh xe khối lượng $m$, có khả năng lăn không trượt, và đầu kia được gắn vào tường. Tìm chu kỳ dao động của hệ thống. Khối lượng của bánh xe phân bố đều trên vành bánh xe.

Hình 1. Hệ lò xo - bánh xe dao động điều hòa

Độ dịch chuyển của tâm bánh xe sang phải đặt là $x$, tại đó chiều quay của bánh xe được quy ước cùng chiều kim đồng hồ.
Cơ năng của hệ $$ E=\frac{1}{2}mv^2+\frac{1}{2}I\omega^2+\frac{1}{2}kx^2 \tag{9} $$ Trong đó, moment quán tính của bánh xe (khối lượng tập trung ở vành bánh xe) là $I=mR^2$, bánh xe lăn không trượt nên $\omega=\frac{v}{R}$. Ta được biểu thức năng lượng đúng chuẩn: $$ E=\frac{1}{2}2mv^2+\frac{1}{2}kx^2 \tag{10} $$ Trong biểu thức năng lượng, khối lượng hiệu dụng là $m_\text{hd}=2m$, còn độ cứng hiệu dụng đúng bằng độ cứng lò xo $k_\text{hd}=k$. Tần số góc, chu kì của dao động là $$ \omega=\sqrt{\frac{k}{2m}}, T=2\pi\sqrt{\frac{2m}{k}} \tag{11} $$

🧠 Ở cấp độ các cuộc thi học sinh giỏi Quốc gia hoặc các kỳ thi Olympic Vật lý, các bài toán sẽ không dễ như Bài toán 1🚀

Tức là biểu thức tính năng lượng sẽ không thể đưa được về dạng mẫu mực (\ref{2}) nếu như không sử dụng một số quy tắc lấy gần đúng. Bởi vì dao động trong các bài toán ở các kì thi này chủ yếu là dao động bé, biên độ dao động là rất nhỏ so với các kích thước liên quan.
Các quy tắc lấy gần đúng thông dụng như: \begin{align} \left(1+\varepsilon\right)^n\approx 1+n\varepsilon, \text{với}\ \varepsilon \ll 1 \end{align} Nếu góc $\alpha$ rất nhỏ thì \begin{align} &\sin{\alpha}\approx \tan{\alpha}\approx \alpha\\ &\cos{\alpha}\approx \left(1-\frac{\alpha^2}{2}\right) \end{align} Thậm chí có lúc lấy $\cos{\alpha}\approx 1$, hoặc bỏ đi các vô cùng bé bậc cao như $\varepsilon^2, \varepsilon^3,...$ tùy vào thực tế mỗi bài toán.

Sau đây chúng ta sẽ cùng giải các bài toán ở cấp độ như vậy.

Bài toán 2. Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của hệ con lắc lò xo - con lắc đơn trong điện trường

Một quả cầu nhỏ khối lượng $m$, mang điện tích $+q$, được treo trên một sợi dây mảnh, không dẫn điện, chiều dài $l$. Một lò xo không dẫn điện, độ cứng $k$, nằm ngang, được gắn vào bên trái quả cầu. Quả cầu nằm trong một điện trường đều $E$, hướng như hình vẽ. Khi cân bằng, sợi dây treo quả cầu treo thẳng đứng. Tìm chu kỳ dao động nhỏ của quả cầu trong mặt phẳng hình vẽ.

Hình 2. Hệ con lắc lò xo - con lắc đơn tích điện trong điện trường

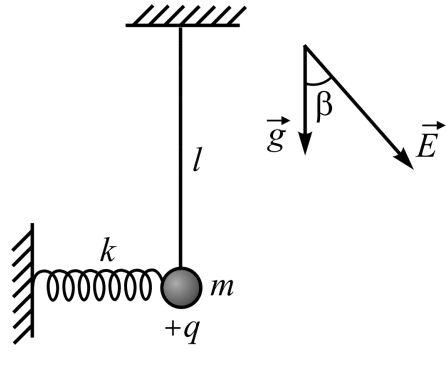
Tại vị trí cân bằng, theo phương ngang (ta đặt trục $Ox$ nằm ngang, có chiều từ trái sang phải), lực đàn hồi cân bằng với thành phần nằm ngang của lực tĩnh điện: $$ k\Delta l_0=qE\sin{\beta} \tag{12} $$ Tại tọa độ $x$, góc lệch của sợi dây là $\alpha=\frac{x}{l}$, với góc nhỏ thì $\sin{\alpha}\approx\alpha$ và $\cos{\alpha}\approx1-\frac{1}{2}\alpha^2$. Ngoài động năng, ta viết thật chi tiết biểu thức các thế năng, đặc biệt là thế năng điện của quả cầu:
Động năng $$ K=\frac{1}{2}mv^2 \tag{13} $$ Thế năng trọng trường được tính tương tự như con lắc đơn, với gốc thế năng tại vị trí cân bằng \begin{align} U_\text{tt}=mgl\left(1-\cos{\alpha}\right) \tag{14} \end{align} Thế năng đàn hồi, với độ biến dạng $\Delta l=\Delta l_0+x=\Delta l_0+\alpha l$: $$ U_\text{đh}=\frac{1}{2}k\left(\Delta l_0+\alpha l\right)^2 \tag{15} $$ Chọn mốc thế năng điện tại vị trí cân bằng thì thế năng điện được tính bằng $-A$, với $A$ là công của lực điện trong quá trình quả cầu đi từ vị trí cân bằng đến tọa độ $x$. Công của lực điện trong điện trường đều là $A=qEd$, với $d$ là độ dịch chuyển của điện tích dọc theo đường sức. Ở đây độ dịch chuyển này được tính bằng $d=l\cos{\left(\beta-\alpha\right)}-l\cos{\beta}$ (như hình 3).

Hình 3. Độ dịch chuyển $d$ dọc theo đường sức

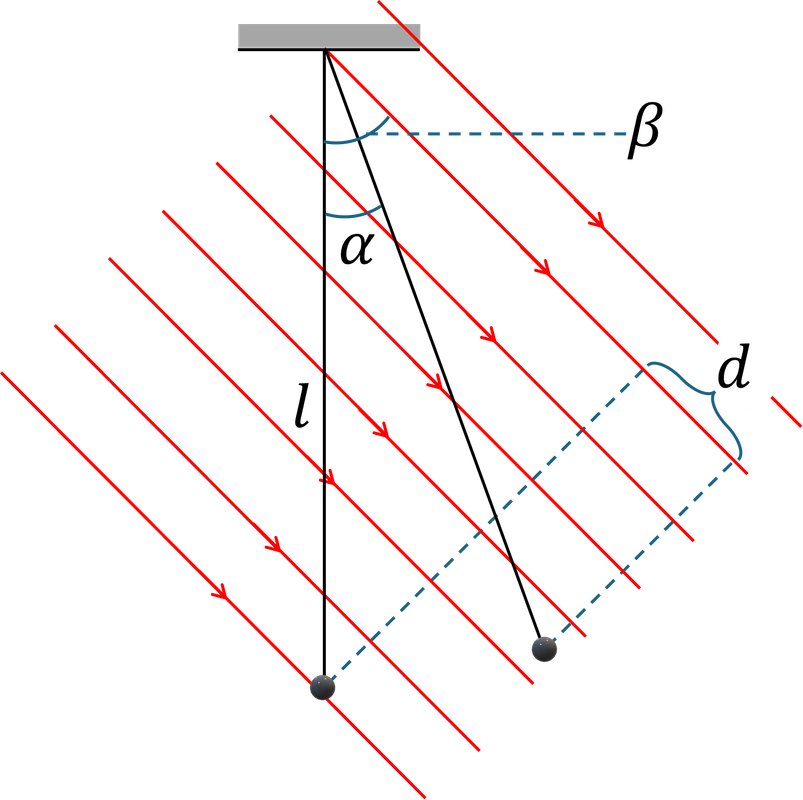
Vậy $$ U_\text{đ}=qEl\left(\cos{\beta}-\cos{\left(\beta-\alpha\right)}\right) \tag{16} $$ Cơ năng của hệ là \begin{align} E=\frac{1}{2}mv^2&+mgl\left(1-\cos{\alpha}\right)\\ &+\frac{1}{2}k\left(\Delta l_0+\alpha l\right)^2\\ &+qEl\left(\cos{\beta}-\cos{\left(\beta-\alpha\right)}\right) \tag{17} \label{17} \end{align} Đến đây có 2 cách cơ bản, có thể đưa về biểu thức cơ năng mẫu mực và lấy khối lượng hiệu dụng và độ cứng hiệu dụng, cũng có thể đạo hàm hai vế theo $t$ rồi đưa phương trình về dạng phương trình dao động điều hòa. Chúng ta chọn cách thứ hai:
Đạo hàm hai vế theo $t$, suy ra \begin{align} 0=mv'v&+mgl\alpha'\sin{\alpha}\\ &+kl\alpha'(\Delta l_0+\alpha l)\\ & -qEl\alpha'\sin{\left(\beta-\alpha\right)} \tag{18} \label{18} \end{align} Trong đó $l\alpha'=v$, tất cả các số hạng đều có đại lượng này nên chúng được rút gọn, và \begin{align} \sin{\alpha}&\approx \alpha,\cos{\alpha}\approx 1-\frac{\alpha^2}{2} \tag{19}\\ \sin{(\beta-\alpha)}&=\sin{\beta}\cos{\alpha}-\cos{\beta}\sin{\alpha}\\ &=\sin{\beta}\left(1-\frac{\alpha^2}{2}\right)-\alpha\cos{\beta} \tag{20}\\ \alpha l&=x \tag{21} \end{align} Biến đổi phương trình (\ref{18}) thành

\begin{align} x''=-\frac{qE\sin{\beta}}{2m}\left(\frac{x}{l}\right)^2-\left(\frac{g}{l}+\frac{k}{m}+\frac{qE\cos{\beta}}{ml}\right)x+\frac{k\Delta l_0}{m}-\frac{qE\sin{\beta}}{m} \tag{22} \end{align}

Phương trình dao động điều hòa đúng thì $x''$ phải là hàm tuyến tính của $x$, nhưng ở đây là hàm bậc hai. Nhiệm vụ tiếp theo là bỏ vô cùng bé bậc hai $\left(\frac{x}{l}\right)^2$, ta còn lại

\begin{align} x''=-\left(\frac{g}{l}+\frac{k}{m}+\frac{qE\cos{\beta}}{ml}\right)x+\frac{k\Delta l_0}{m}-\frac{qE\sin{\beta}}{m} \tag{23} \end{align}

Suy ra tần số góc $$ \omega=\sqrt{\frac{g}{l}+\frac{k}{m}+\frac{qE\cos{\beta}}{ml}} \tag{24} $$

😮‍💨 Lời giải trên hơi dài và khá rối, phải không? Đó là nhược điểm của cách làm gần đúng thông thường. Nhưng may mắn là còn một hướng tiếp cận khác — ngắn gọn hơn, tinh tế hơn.🌤️

Trước hết chúng ta phải hiểu thế nào là dao động bé✨
🤔Dao động trong phạm vi nào thì được gọi là dao động bé?
🙇‍♀️Các phép lấy gần đúng phải đảm bảo được yêu cầu gì? Tại sao khi thì lấy được $\cos{\alpha}\approx 1$, khi thì phải lấy $\cos{\alpha}\approx 1-\frac{\alpha^2}{2}$? Khi nào thì bỏ vô cùng bé bậc hai, khi nào thì không?

Phạm vi thì có ngay sau đây, còn phép lấy gần đúng thì chẳng cần, chỉ cần làm theo các bước sau đây 👉

Việc viết biểu thức năng lượng của hệ phải làm một cách chính xác, không áp dụng phép lấy gần đúng nào hết. Ở Bài toán 2 ta đã viết được công thức tính năng lượng, đó là phương trình (\ref{17}). Bạn hãy viết lại phương trình này vào giấy nháp để tiếp tục cùng tôi nghiên cứu nhé.
Lấy đạo hàm hai vế phương trình (\ref{17}) theo thời gian, ta sẽ được phương trình (\ref{18}). Chú ý $l\alpha'=v$ và $v'=l\alpha''$, từ (\ref{18}) suy ra

\begin{align} \alpha''=-\frac{g}{l}\sin{\alpha}-\frac{k}{m}\left(\frac{\Delta l_0}{l}+\alpha\right)+\frac{qE}{ml}\sin{\left(\beta-\alpha\right)}\tag{25}\label{25} \end{align}

Rõ ràng (\ref{25}) không phải là phương trình dao động điều hòa. Bởi vì chúng ta đang xét tọa độ $\alpha$ của quả cầu ở phạm vi bất kì, chưa phải góc nhỏ. Đồ thị $\alpha''(\alpha)$ biểu diễn mối liên hệ giữa $\alpha''$ và $\alpha$ của (\ref{25}) là đường cong màu xanh nhạt trong Hình 4. Trong khi phương trình dao động điều hòa phải có dạng $\alpha''=-\omega^2\alpha$, tức là đồ thị $\alpha''(\alpha)$ phải là một đường thẳng với hệ số góc bằng $-\omega^2$.

Hình 4. Đoạn đồ thị màu đen đậm nằm trên cả đường cong và đường thẳng

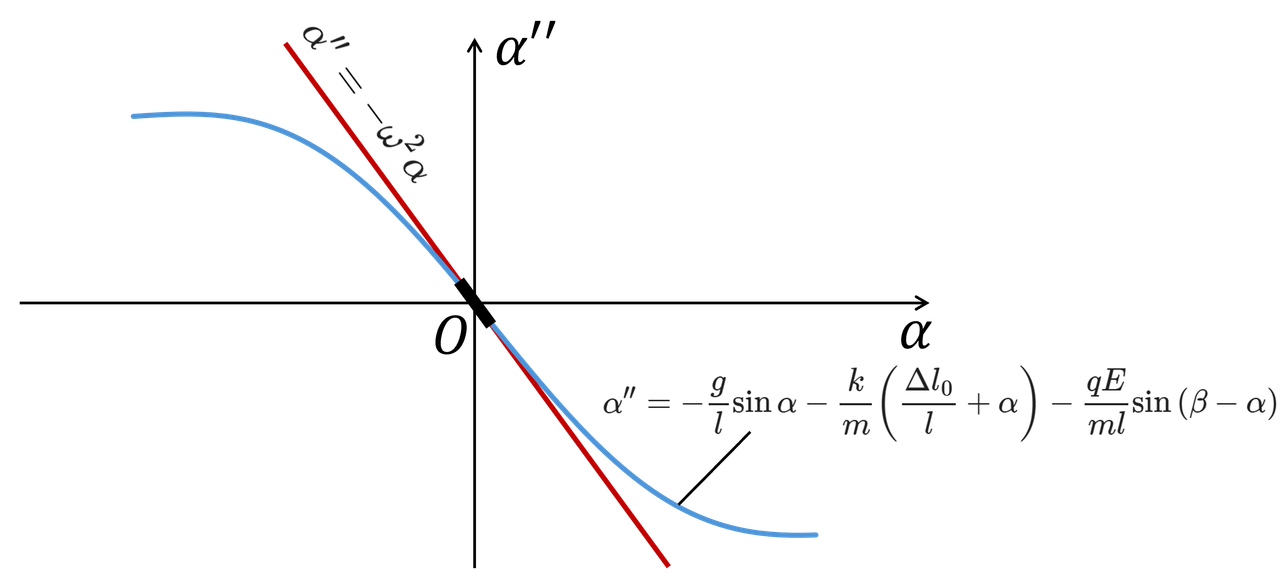
Khi xét dao động bé xung quanh vị trí cân bằng ($\alpha=0$) thì chúng ta chỉ quan tâm đến một đoạn đồ thị rất ngắn lân cận của $\alpha=0$, đoạn đồ thị đó chính là một đoạn thẳng (đoạn màu đen đậm trong Hình 4). Có nghĩa là trong phạm vi này quả cầu dao động điều hòa.
Đoạn đồ thị này cũng nằm trên đường thẳng tiếp tuyến với đường cong tại $\alpha=0$ nên nó có hệ số góc bằng $$ -\omega^2=\left.\frac{d\alpha''}{d\alpha}\right|_{\alpha=0} $$ Ở Bài toán 2 này thì

\begin{align} \frac{d\alpha''}{d\alpha}&=-\frac{g}{l}\cos{\alpha}-\frac{k}{m}-\frac{qE}{ml}\cos{\left(\beta-\alpha\right)}\tag{26}\label{26}\\ -\omega^2=\left.\frac{d\alpha''}{d\alpha}\right|_{\alpha=0}&=-\left(\frac{g}{l}+\frac{k}{m}+\frac{qE}{ml}\cos{\beta}\right)\tag{27}\label{27}\\ \omega&=\sqrt{\frac{g}{l}+\frac{k}{m}+\frac{qE}{ml}\cos{\beta}} \end{align}

👉Tóm lại, để tìm chu kì dao động bé bằng phương pháp năng lượng, chúng ta chỉ cần thực hiện các bước sau đây:

1. Viết biểu thức tính năng lượng của hệ ở tọa độ $x$.
2. Đạo hàm hai vế phương trình năng lượng.
3. Rút gọn thành phần $v$, $x'$ vì chắc chắn số hạng nào cũng có.
4. Suy ra biểu thức $x''(x)$
5. Tính đạo hàm $f(x)=\frac{dx''}{dx}$.
6. Có ngay tần số góc $\omega=\sqrt{-f'(x_0)}$

Bây giờ hãy theo các bước vừa nêu để giải các bài toán tìm chu kì dao động bé bằng phương pháp năng lượng nhé!

Bài toán 3. Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của hệ con lắc lò xo - cấu trúc khớp nối

Kết cấu (hình 5) gồm ba quả cầu nhỏ giống hệt nhau, mỗi quả có khối lượng $𝑚$, được nối với nhau bằng các thanh nhẹ có chiều dài $𝑙$. Ở vị trí cân bằng, kết cấu được giữ bởi một lò xo thẳng đứng có độ cứng $𝑘$ và có dạng hình vuông. Xác định chu kỳ $𝑇$ của dao động bé theo phương thẳng đứng của quả cầu dưới cùng.

Hình 5. Hệ con lắc lò xo - cấu trúc khớp nối

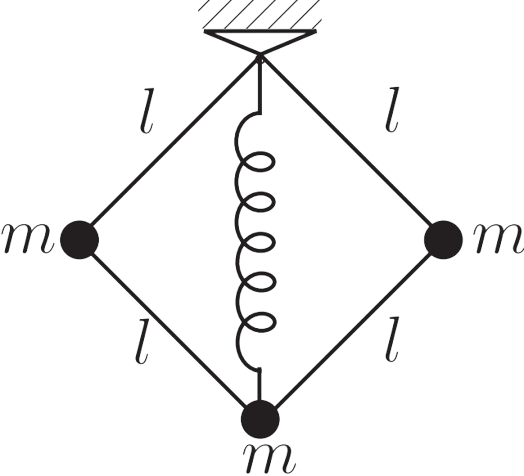
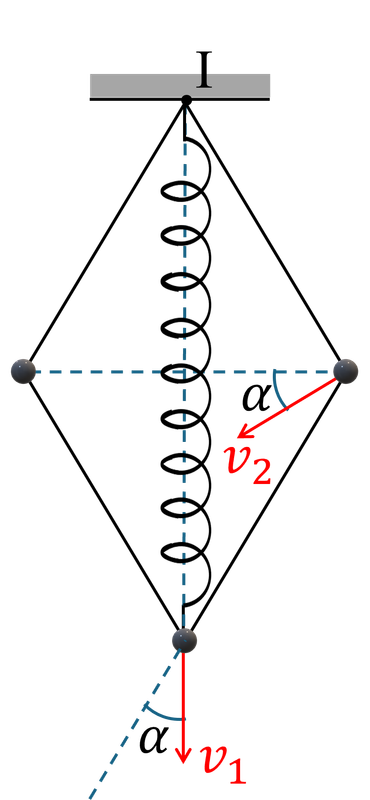
Chúng ta cân nhắc việc chọn biến số trong quá trình dao động của hệ, đó là tọa độ $x$ của vật dưới cùng hay tọa độ góc của một thanh. Ở đây chọn biến số là góc $\alpha$ giữa các thanh với phương thẳng đứng có vẻ như thuận lợi hơn. Mốc thế năng trọng trường ta cũng chọn chung tại điểm treo. Tại một vị trí của hệ, nơi có góc $\alpha$, vận tốc các vật là $v_1$ và $v_2$ (hình 6), ta có năng lượng của hệ

\begin{align} K&=\frac{1}{2}mv_1^2+2\frac{1}{2}mv_2^2\\ U&=\frac{1}{2}k(\Delta l_0+2l\cos{\alpha}-l\sqrt{2})^2-mg2l\cos{\alpha}-2mgl\cos{\alpha}\tag{28}\label{28} \end{align}

Hình 6. Vị trí của các vật được xác định bởi góc lệch $\alpha$ giữa các thanh với phương thẳng đứng

Trong đó $\Delta l_0$ là độ biến dạng của lò xo ở vị trí cân bằng, nó được xác định bằng phương trình $\frac{dU}{d\alpha}=0$ khi $\alpha=45^\text{o}$. $$\Delta l_0=\frac{2mg}{k}$$

Trong (\ref{28}) có biến tọa độ $\alpha$ nhưng có đến hai biến vận tốc $v_1$ và $v_2$. Nhiệm vụ tiếp theo là phải liên hệ hai vận tốc này với nhau để đưa chúng về một biến.
Hãy vẽ hình thật cẩn thận và viết các biểu thức liên hệ một cách chính xác. Hình 6 thể hiện rất rõ ràng: quả cầu dưới cùng luôn chuyển động theo phương thẳng đứng (do tính đối xứng) nên $\vec{v}_1$ hợp với các thanh gắn với vật góc $\alpha$; hai quả cầu còn lại như hai con lắc đơn với điểm treo $\text{I}$, vận tốc $\vec{v}_2$ luôn vuông góc với thanh gắn với quả cầu, nên nó tạo với phương nagng góc $\alpha$.
Mặt khác hai quả cầu cùng nẳm trên một thanh nên vận tốc của chúng tuân theo biểu thức \begin{align} v_1\cos{\alpha}&=v_2\cos{\left(90^\text{o}-2\alpha\right)}\\ &=v_2\sin{(2\alpha)}\\ &=2v_2\sin{\alpha}\cos{\alpha}\\ \Rightarrow v_1&=2v_2\sin{\alpha}\tag{29}\label{29} \end{align} Đặt $v_2=v$ thì $v_1=2v\sin{\alpha}$.
Đến đây ta đã có biểu thức năng lượng

\begin{align} E=mv^2\left(2\sin^2{\alpha}+1\right)+\frac{1}{2}k\left(\Delta l_0+2l\cos{\alpha}-l\sqrt{2}\right)^2-4mgl\cos{\alpha}\tag{30}\label{30} \end{align}

Đạo hàm hai vế theo thời gian ta có

\begin{align} 0&=2mvv'(2\sin^2{\alpha}+1)+mv^2\alpha'4\sin{\alpha}\cos{\alpha}\\ & -\frac{1}{2}kl^22(2\cos{\alpha}-\sqrt{2})2\alpha'\sin{\alpha}\\ &+4mgl\alpha'\sin{\alpha} \end{align}

Chú ý rằng $v=l\alpha'$, rút gọn các thành phần này trên tất cả các số hạng, ta được

\begin{align} 0&=2ml\alpha''(2\sin^2{\alpha}+1)+2mv^2\sin{2\alpha}\\ & -2kl^2(2\cos{\alpha}-\sqrt{2})\sin{\alpha}\\ &+4mgl\sin{\alpha}\tag{31}\label{31} \end{align}

Bước tiếp theo là suy ra biểu thức $\alpha''=f(\alpha)$
Tuy nhiên ở bài toán này, từ (\ref{31}) suy ra biểu thức $\alpha''$ vẫn còn chứa $v$. Thật là bực phải không! Nhưng không sao, bỏ nó đi là được. Nhưng bỏ thế nào cho hợp lý? Ta hãy trở lại phương trình (\ref{30}) và nhận thấy rằng, trong động năng không chỉ có $v^2$ mà có cả $\alpha$, điều này làm cho phương trình sau khi đạo hàm không thể rút gọn được hết $v$. Ta suy luận như sau:
Do dao động rất bé nên ta xem như hướng vận tốc của các quả cầu bên trên thay đổi không đáng kể, nó luôn hợp với phương ngang một góc $45^\text{o}$ như ban đầu. Tức là $v_1=2v_2\sin{45^\text{o}}$. Nếu đặt $v_2=v$ thì $v_1=v\sqrt{2}$, và biểu thức năng lượng sẽ là

\begin{align} E=2mv^2+\frac{1}{2}k\left(\Delta l_0+2l\cos{\alpha}-\sqrt{2}l\right)^2-4mgl\cos{\alpha}\tag{32}\label{32} \end{align}

Đạo hàm hai vế theo thời gian ta có

\begin{align} 0&=4mvv'\\ & -2kl\alpha'(2l\cos{\alpha}-\sqrt{2}l+\Delta l_0)\sin{\alpha}\\ &+4mgl\alpha'\sin{\alpha} \end{align}

Sau khi rút gọn $v=l\alpha'$ và đổi $v'=l\alpha''$, ta suy ra

\begin{align} f(\alpha)=\alpha''=\frac{k}{2m}\sin{\alpha}\left(2\cos{\alpha}-\sqrt{2}+\frac{\Delta l_0}{l}\right)-\frac{g}{l}\sin{\alpha}\tag{33}\label{33}\\ f'(\alpha)=\frac{d\alpha''}{d\alpha}=\frac{k}{2m}\left[2\cos{2\alpha}-\left(\sqrt{2}-\frac{\Delta l_0}{l}\right)\cos{\alpha}\right]-\frac{g}{l}\cos{\alpha}\tag{34}\label{34}\\ \end{align}

Nhớ rằng $\Delta l_0=\frac{2mg}{k}$ và $\omega=\sqrt{-f'(45^\text{0})}$, ta có tần số góc $$ \omega=\sqrt{\frac{k}{2m}} $$

👉Kinh nghiệm rút ra từ bài toán 3:

1. Nếu biểu thức động năng có chứa tọa độ thì lập luận làm triệt tiêu chúng, đảm bảo động năng chỉ còn vận tốc.
2. Nếu thế năng có chứa vận tốc thì lập luận làm triệt tiêu chúng, đảm bảo thế năng chỉ còn tọa độ.

Bài toán 4. Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của quả cầu tích điện trong điện trường của hai điện tích điểm cố định

Giữa hai hạt tích điện $𝑄_1$ và $𝑄_2$, cách nhau một khoảng $𝐿$, có một hạt tích điện $𝑞$ và khối lượng $𝑚$. Cả ba hạt có điện tích cùng dấu và nằm trên cùng một đường thẳng. Vị trí của các hạt có điện tích $𝑄_1$ và $𝑄_2$ là cố định, chúng không thể chuyển động. Hạt có điện tích $𝑞$ chỉ có thể chuyển động không ma sát dọc theo đường thẳng đi qua cả ba hạt. Tìm tần số dao động điều hòa nhỏ của hạt có điện tích $𝑞$ khi lệch khỏi vị trí cân bằng nhỏ hơn nhiều so với khoảng cách từ vị trí cân bằng đến mỗi hạt có điện tích $𝑄_1$ và $𝑄_2$. Bỏ qua từ trường sinh ra bởi chuyển động của các điện tích. .

Hình 7. Hạt tích điện dao động bé giữa hai hạt tích điện cố định

Đặt khoảng cách từ $Q_1$ đến $q$ là $x$, khi đó khoảng cách từ $Q_2$ đến $q$ là $L-x$. Ta xét hệ tại vị trí cân bằng của $q$, lực đẩy tĩnh điện từ các điện tích $Q_1$ và $Q_2$ lên $q$ có độ lớn bằng nhau, suy ra

$$ \frac{Q_1}{x_0^2}=\frac{Q_2}{(L-x_0)^2}\\ \frac{\sqrt{Q_1}}{x_0}=\frac{\sqrt{Q_2}}{L-x_0}=\frac{\sqrt{Q_1}+\sqrt{Q_2}}{L}\\ $$

\begin{align} x_0&=\frac{\sqrt{Q_1}}{\sqrt{Q_1}+\sqrt{Q_2}}L\tag{35}\label{35}\\ L-x_0&=\frac{\sqrt{Q_2}}{\sqrt{Q_1}+\sqrt{Q_2}}L\tag{36}\label{36} \end{align}

Cơ năng của quả cầu $q$ tại tọa độ $x$ là \begin{align} E&=\frac{1}{2}mv^2\\ &+\frac{kqQ_1}{x}+\frac{kqQ_2}{L-x}\tag{37}\label{37} \end{align} Đạo hàm hai vế (\ref{37}) theo thời gian ta được \begin{align} 0=mvv'-\frac{kqQ_1x'}{x^2}+\frac{kqQ_2x'}{(L-x)^2} \end{align} Rút gọn các thành phần vận tốc và suy ra gia tốc $$ x''=-\frac{kq}{m}\left[\frac{Q_2}{(L-x)^2}-\frac{Q_1}{x^2}\right]\\ f(x)=-\frac{dx''}{dx}=\frac{2kq}{m}\left[\frac{Q_2}{(L-x)^3}+\frac{Q_1}{x^3}\right]\tag{38}\label{38} $$ Trở lại (\ref{35}) và (\ref{36}) để lấy $x_0$ và $L-x_0$ để thay vào (\ref{38}), ta được $$ f(x_0)=-\frac{2kq}{mL^3}\frac{\left(\sqrt{Q_1}+\sqrt{Q_2}\right)^4}{\sqrt{Q_1Q_2}} $$ Tần số góc của dao động bé của quả cầu điện tích $q$ là $$ \omega=\sqrt{-f(x_0)}=\left(\sqrt{Q_1}+\sqrt{Q_2}\right)^2\sqrt{\frac{2kq}{mL^3\sqrt{Q_1Q_2}}} $$

Bài toán 5. Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của hệ hình trụ lăn trên nêm tự do

Trên mặt sàn nằm ngang có vật A có khối lượng $M$, mặt dưới phẳng, mặt trên lõm là một phần của mặt trụ bán kính $R$. Vật B có dạng hình trụ đặc bán kính $r$, khối lượng $m$. Đặt vật B trên mặt lõm của vật A sao cho trục của nó song song với trục của mặt trụ lõm này. Lúc đầu vật A đứng yên trên mặt sàn, vật B được giữ ở vị trí sao bán kính của mặt trụ lõm cắt trục của khối trụ A hợp với phương thẳng đứng một góc $\alpha_0$ ($\alpha_0$ có giá trị rất nhỏ). Thả cho B chuyển động với vận tốc ban đầu bằng không. Ma sát giữa A và mặt sàn không đáng kể, ma sát gữa A và B đủ lớn để B lăn không trượt trên mặt trụ lõm của A. Cho gia tốc trọng trường là $g$. Tính chu kì dao động của hệ.

Hình 8. Hình trụ lăn trên nêm tự do

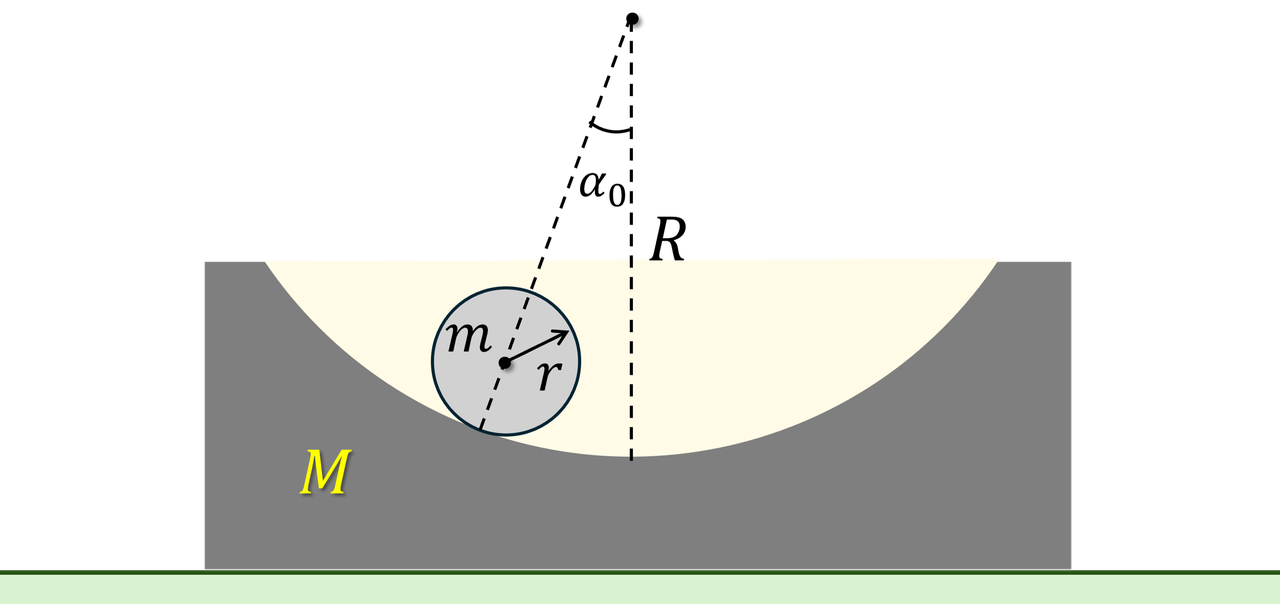
Trong hệ quy chiếu gắn với vật A, khi khối trụ B ở tọa độ góc $\alpha$ nó có tốc độ góc $\omega$ ứng với vận tốc $v_1=r\omega$. Trong hệ quy chiếu gắn với mặt sàn thì vận tốc theo phương ngang của B là $v_x =r\omega\cos{\alpha}+V$, với $V$ là vận tốc của A.
Áp dụng định luật bảo toàn động lượng theo phương ngang ta có $$ MV+mv_x=0\\ V=-\frac{mr\omega\cos{\alpha}}{m+M} $$ Cơ năng của hệ

$$ E=\frac{1}{2}MV^2+\frac{1}{2}mv_x^2+\frac{1}{2}mv_y^2+\frac{1}{2}I\omega^2-mgR\cos{\alpha} $$

Ở đây ta đã chọn mốc thế năng ở trục của mặt trụ lõm. Vận tốc theo phương thẳng đứng của vật B là $v_y=r\omega\sin{\alpha}$. Moment quán tính của khối trụ đặc $I=\frac{1}{2}mr^2$. Rút kinh nghiệm từ Bài toán 3, trong biểu thức tính năng lượng nếu trong động năng có cả tọa độ và vận tốc thì phải lập luận làm mất thành phần tọa độ đi. Ở đây ta thấy trong tất cả các thành phần động năng đều có cả vận tốc góc $\omega$ và tọa độ $\alpha$.
Ta lập luận rằng, góc dao động rất nhỏ nên thành phần vận tốc theo phương thẳng đứng của vật B không đáng kể, hay nói cách khác vector vận tốc của B chỉ theo phương ngang $v=\omega r+V$. Vận tốc của A là $V=-\frac{mr\omega}{m+M}$. Năng lượng của hệ bây giờ là

\begin{align} E&=\frac{1}{2}M\left(\frac{mr\omega}{m+M}\right)^2+\frac{1}{2}m\left(r\omega\right)^2+\frac{1}{2}\left(\frac{1}{2}mr^2\right)\omega^2-mgR\cos{\alpha}\\ &=\frac{1}{2}mr^2\left(\frac{mM}{\left(m+M\right)^2}+\frac{3}{2}\right)\omega^2-mgR\cos{\alpha}\tag{39}\label{39} \end{align}

Đạo hàm hai vế (\ref{39}) theo thời gian ta được

\begin{align} 0=mr^2\left(\frac{mM}{\left(m+M\right)^2}+\frac{3}{2}\right)\omega\omega'+mgR\alpha'\sin{\alpha} \end{align}

Rút gọn thành phần $\alpha'=\omega$ đồng thời chú ý rằng $\omega'=\alpha''$ và $\sin{\alpha}\approx\alpha$ ta được $$ \alpha''=-\frac{gR}{r^2\left(\frac{mM}{\left(m+M\right)^2}+\frac{3}{2}\right)}\alpha\\ \omega=\sqrt{\frac{gR}{r^2\left(\frac{mM}{\left(m+M\right)^2}+\frac{3}{2}\right)}} $$

BÀI TẬP THỰC HÀNH ÁP DỤNG PHƯƠNG PHÁP NĂNG LƯỢNG TÌM CHU KÌ DAO ĐỘNG ĐIỀU HÒA NHỎ

Bài tập 1: Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của con lắc lò xo trượt trên mặt phẳng nghiêng

Trên một mặt phẳng nghiêng tạo với phương ngang một góc $\alpha$, có một lăng trụ khối lượng $M$, tựa vào mặt thẳng đứng của lăng trụ một thanh có khối lượng không đáng kể (xem Hình 9). Thanh được gắn chặt vào tường bằng một lò xo có độ cứng $k$, do có khe dẫn hướng, thanh chỉ có thể chuyển động theo phương ngang. Bỏ qua ma sát giữa lăng trụ và mặt phẳng nghiêng, lăng trụ và thanh, thanh và các thanh dẫn hướng. Hãy tìm chu kỳ dao động của lăng trụ.

Hình 9. Con lắc lò xo trượt trên mặt phẳng nghiêng

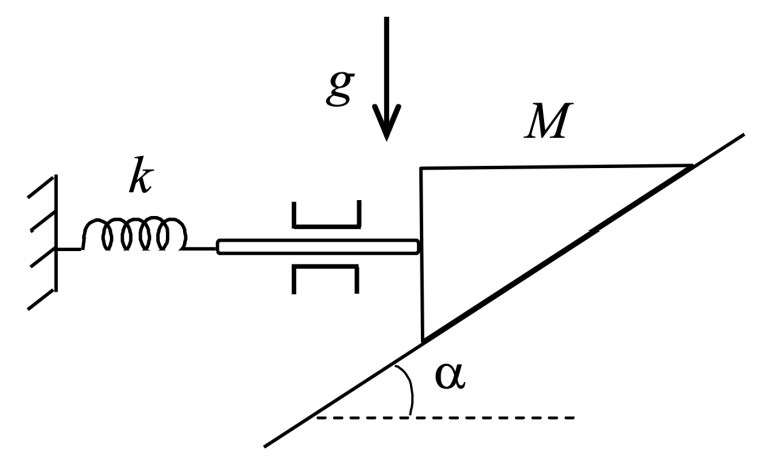
Bài tập 2: Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của con lắc đơn có điểm treo tự do

Một sợi dây lý tưởng có chiều dài $L$ nối một vòng tròn có thể trượt không ma sát dọc theo một nan hoa nằm ngang cố định và một vật nặng có khối lượng gấp đôi vòng tròn. Ban đầu, vòng tròn và vật nặng được giữ ở vị trí mà sợi dây tạo thành một góc nhỏ với phương thẳng đứng (xem Hình 10), sau đó thả nhẹ để hệ dao động điều hòa. Tìm chu kỳ dao động của hệ. Giả sử gia tốc rơi tự do $g$ đã biết.

Hình 10. Con lắc đơn có điểm treo tự do

Bài tập 3: Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của hệ đòn bẩy lò xo

Hai đầu đòn bẩy không trọng lượng được đặt các chất điểm có khối lượng $m_1$ và $m_2$, đồng thời gắn các lò xo không trọng lượng có độ cứng $k_1$ và $k_2$. Khoảng cách từ hai đầu đòn bẩy đến điểm tựa lần lượt bằng $l_1$ và $l_2$. Chiều dài của các lò xo ở trạng thái không biến dạng được chọn sao cho đòn bẩy cân bằng ở vị trí nằm ngang. Tìm tần số dao động nhỏ của đòn bẩy sau khi lệch một chút so với phương ngang. Đòn bẩy không rời khỏi điểm tựa trong suốt quá trình dao động. Chiều dài của các lò xo lớn hơn nhiều so với biên độ dao động.

Hình 11. hệ đòn bẩy lò xo

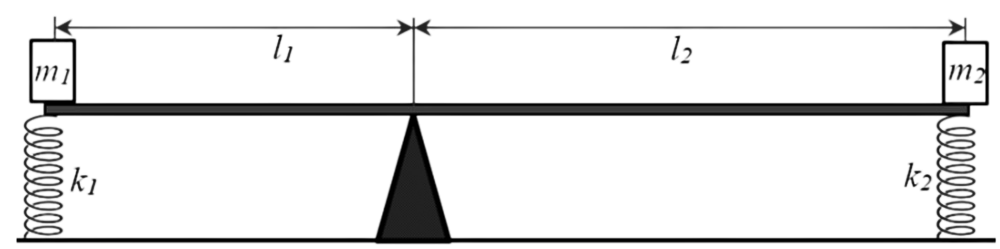
Bài tập 4: Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của hệ vòng tròn quay liên kết chất điểm trượt thẳng

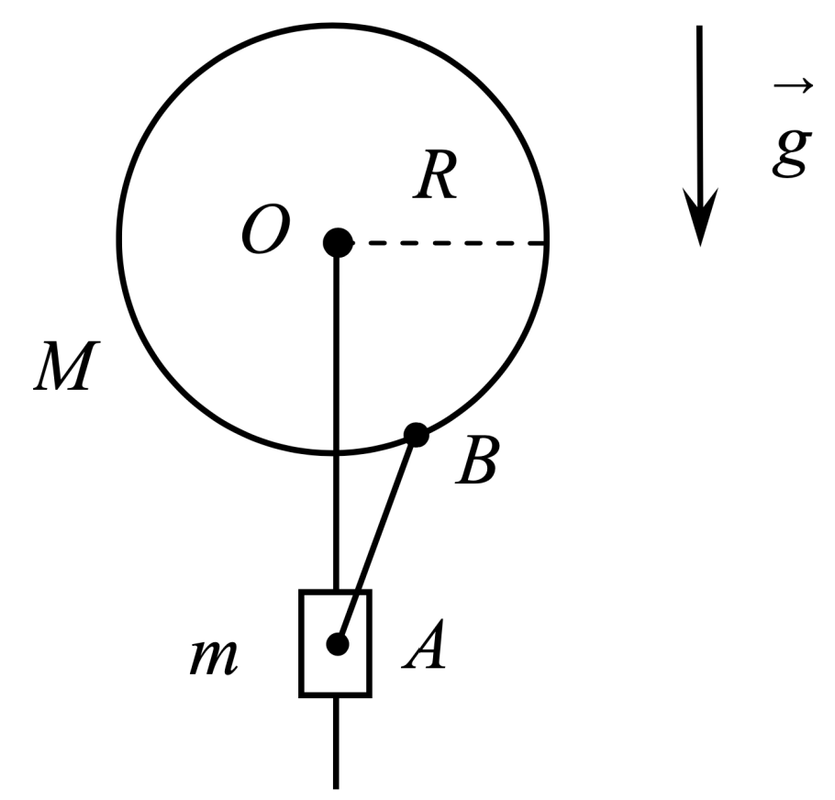
Một vật có khối lượng $m = 10\ \text{g}$ có thể trượt dọc theo một thanh dẫn thẳng đứng cố định. Một vành tròn mảnh đồng chất khối lượng $M=90\ \text{g}$ có trục quay O cố định nằm ngang gắn ở đầu trên của thanh dẫn (vành được liên kết với trục O nhờ những nan hoa nhẹ không được vẽ trong hình 11). Bán kính của vành là $R = 20\ \text{cm}$. Vành và vật nặng được nối với nhau bằng một thanh cứng $\text{AB}$ không trọng lượng, có thể quay tự do quanh các điểm gắn $\text{A}$ và $\text{B}$. Chiều dài của thanh $L = \text{AB} = 16\ \text{cm}$. Ở vị trí cân bằng, vành được đặt sao cho thanh $\text{AB}$ thẳng đứng. Tìm chu kỳ $T$ của các dao động của hệ xảy ra khi vòng lệch nhỏ so với vị trí này. Coi vật là một chất điểm, bỏ qua ma sát. Gia tốc trọng trường $g = 10\ \text{m/s}^2$.

Hình 11. Hệ vòng tròn quay liên kết chất điểm trượt thẳng

Bài tập 5: Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của vành có gắn vật nặng lăn không trượt trên mặt bàn

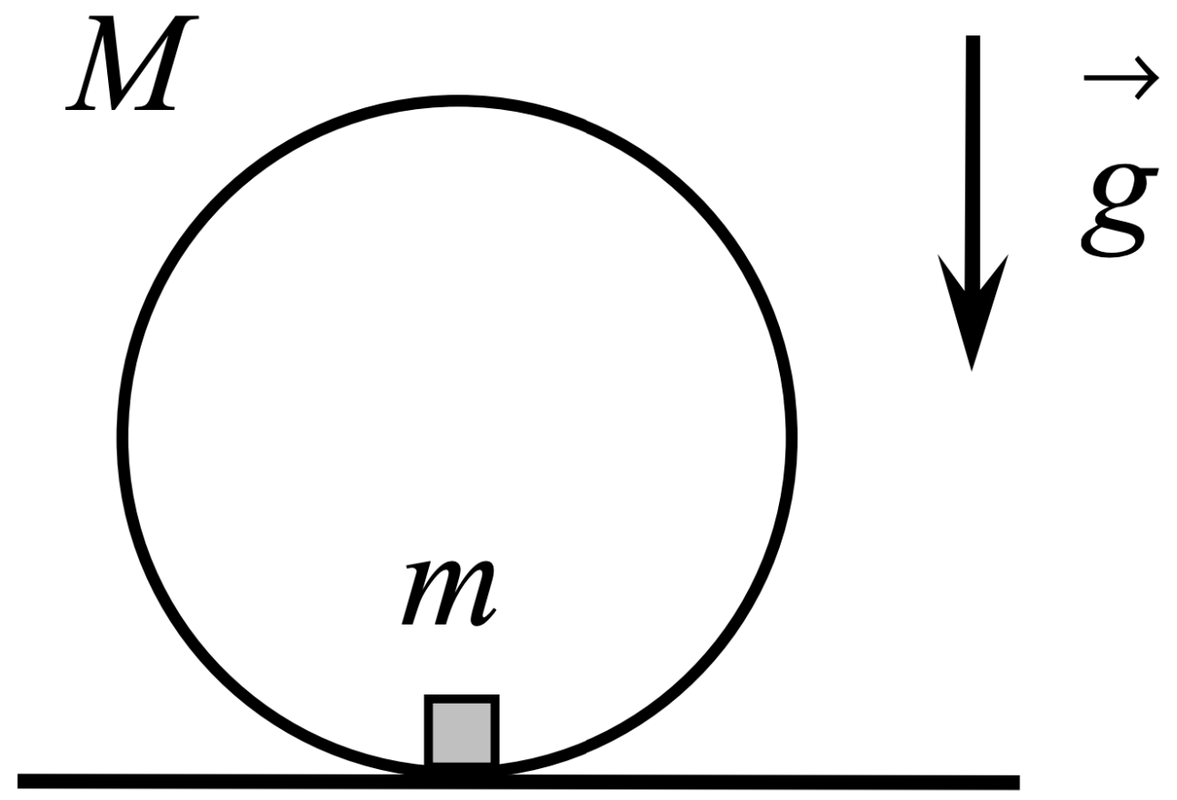
Một chiếc vòng mảnh có khối lượng $M = 50\ \text{g}$ và bán kính $R = 0\text{,}1\ \text{m}$ được đặt thẳng đứng trên một mặt bàn nằm ngang. Khối lượng của vòng phân bố đều dọc theo chiều dài. Một nhỏ vật có khối lượng $m = 4\ \text{g}$ được gắn vào mặt trong của vòng. Ở vị trí cân bằng, vật nặng nằm ở điểm thấp nhất của vòng. Tìm chu kỳ $T$ của các dao động nhỏ của vòng quanh vị trí này. Giả sử vòng lăn trên bàn không trượt. Gia tốc trọng trường là $g = 10\ \text{m/s}^2$.

Hình 12. Vành có gắn vật nặng lăn không trượt trên mặt bàn

Bài tập 6: Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của đĩa lăn không trượt trên máng cong hình elip

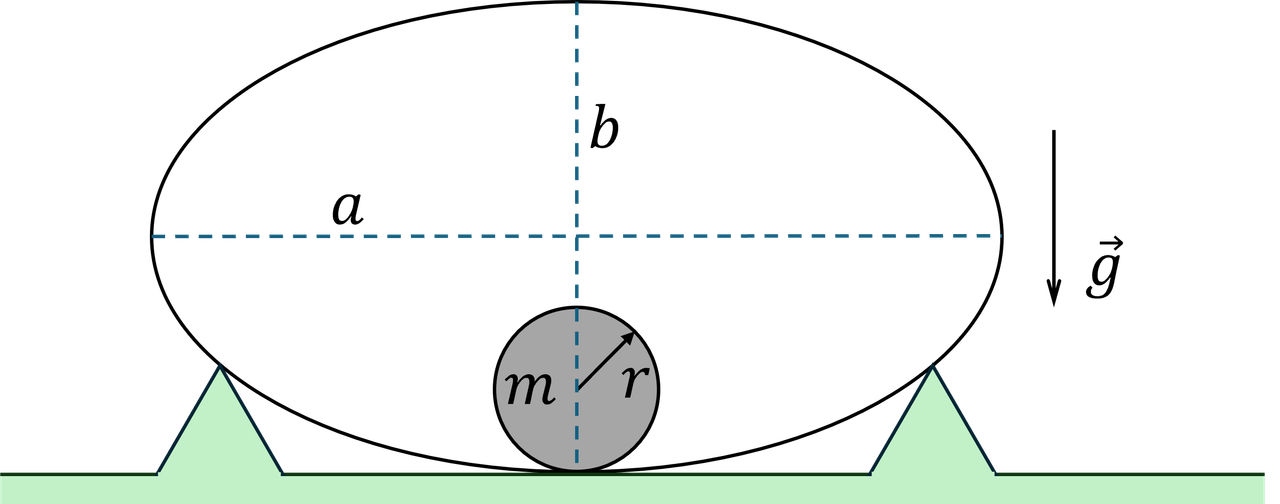
Tìm chu kỳ dao động nhỏ của một hình trụ thành mỏng bán kính $r$ có thể lăn không trượt dọc theo một ống cố định có tiết diện ngang hình elip có bán trục lớn $a$, bán trục nhỏ $b$ $(a\ll r, b\ll r)$. Vị trí của ống so với phương thẳng đứng được thể hiện trong hình 13.

Hình 13. Đĩa lăn không trượt trên máng cong hình elip

Bài toán 7. Dùng phương pháp năng lượng tìm chu kì dao động điều hòa của hệ hình trụ lăn trên máng tự do

Cho vật 1 là một bản mỏng đều, đồng chất, được uốn theo dạng lòng máng thành một phần tư hình trụ AB cứng, ngắn, có trục $∆$, bán kính $R$ và được gắn với điểm $\text{O}$ bằng các thanh cứng, mảnh, nhẹ. Vật 1 có thể quay không ma sát quanh một trục cố định (trùng với trục $∆$) đi qua điểm $\text{O}$. Trên Hình 8, $\text{OA}$ và $\text{OB}$ là các thanh cứng cùng độ dài $R$, $\text{OAB}$ nằm trong mặt phẳng vuông góc với trục $∆$,chứa khối tâm $\text{G}$ của vật 1, $\text{C}$ là giao điểm của $\text{OG}$ và lòng máng.

Hình 14. Hình trụ lăn trên máng tự do

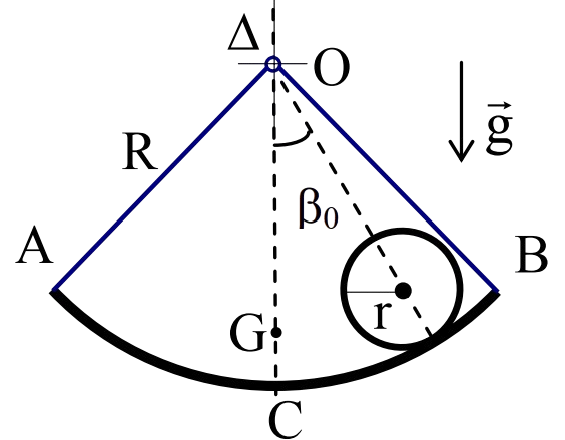
1. Tìm vị trí khối tâm G của vật 1.
2. Giữ cho vật 1 đứng yên tại vị trí cân bằng rồi đặt trên nó vật 2 là một hình trụ rỗng, mỏng, đồng chất, cùng chiều dài với vật 1, bán kính $r$ $(r \lt R)$, nằm dọc theo đường sinh của vật 1. Kéo vật 2 lệch ra khỏi vị trí cân bằng một góc nhỏ $β_0$ rồi thả nhẹ đồng thời cả hai vật. Tìm chu kì dao động nhỏ của vật 2. Biết rằng trong quá trình dao động, vật 2 luôn lăn không trượt trên vật 1.

ĐÁP SỐ CÁC BÀI TẬP THỰC HÀNH

🧠 Các bạn gửi lời giải để mình đăng (và nêu tên tác giả) để mọi người cùng tham khảo nhé.
🚀 Hãy chia sẻ lời giải của mình về địa chỉ: emailcuanguyendinhtan@gmail.com

💖 Ủng hộ tác giả

💡 Nếu bạn cần tài liệu, khóa học ôn thi học sinh giỏi môn Vật lý thì liên hệ mua theo địa chỉ: emailcuanguyendinhtan@gmail.com
☕ Nếu bạn thấy bài viết hữu ích, bạn có thể ủng hộ mình qua nút Donate bên dưới.
🚀 Ngoài ra, blog được duy trì nhờ quảng cáo, bạn cũng có thể quan tâm đến các quảng cáo xuất hiện trên trang.

☕ Donate ngay