
Đạo hàm có ý nghĩa rất quan trọng trong việc giải các bài tập vật lí. Nhưng trong hầu hết các bài toán, nếu ứng dụng ý nghĩa hình học của đạo hàm, thì chúng ta thường đề cập đến đạo hàm bậc nhất. Bài viết này, tác giả xin giới thiệu ý nghĩa hình học của đạo hàm cấp hai, và ứng dụng của nó trong việc giải quyết một số bài toán vật lí.
Chúng ta sẽ bắt đầu từ đạo hàm bậc nhất
Xét hàm số $y=f\left(x\right)$ có một phần đồ thị như hình vẽ dưới đây (đường cong):
\begin{align} \tan{\alpha} &=\frac{dy}{dx}=y^\prime\left(x\right)\\ &=\lim\limits_{\Delta x\rightarrow0}{\frac{f\left(x+\Delta x\right)-f\left(x\right)}{\Delta x}}\tag{2} \end{align} Đây chính là đạo hàm của hàm số $y = f(x)$
Về mặt hình học, đạo hàm của hàm số tại một điểm nào đó, chính là hệ số góc của đường tiếp tuyến của đồ thị tại điểm đó. Tức là:
Ý nghĩa hình học của đạo hàm cấp hai
1. Đạo hàm cấp hai
\begin{align} y^{\prime\prime}&=\left(y^\prime\left(x\right)\right)^\prime\\ &=\frac{d\left(\frac{dy}{dx}\right)}{dx}\\ &=\lim\limits_{\Delta x\rightarrow0}{\frac{f^\prime\left(x+\Delta x\right)-f\prime\left(x\right)}{\Delta x}}\\ &=\frac{d^2y}{dx^2}\tag{3} \end{align}2. Ý nghĩa hình học của đạo hàm bậc hai
Như đã biết, “độ dốc” của đồ thị được xác định bằng đạo hàm bậc nhất. Bây giờ ta đặt ra câu hỏi, liệu có xác định được “độ cong” của đồ thị tại mỗi điểm hay không.

Cũng cần lưu ý rằng, trong biểu thức tính bán kính cong $r$ thì $ds > 0$, nhưng dα có thể dương (nếu bề lõm của đồ thị hướng lên trên) hoặc âm (nếu bề lõm quay xuống dưới). Tức là:
Một số bài toán minh họa
Bài 1
Một hòn bi nhỏ khối lượng $m$ bắt đầu lăn từ điểm $O$ trên một máng trơn $OCB$ như hình vẽ. Hãy tính áp lực của bi lên máng tại $C$ biết hình cắt của máng là một đường được xác định bằng phương trình $y = h\sin{\frac{πx}{l}}$, với $h = \frac{l}{3}$.

Giải
Trước hết ta xác định độ dốc của máng tại $\text{C}$ \begin{align} \frac{dy}{dx}=\frac{\pi h}{l}\cos{\left(\frac{\pi x}{l}\right)}\tag{9} \end{align} Tại điểm $\text{C}$ thì $x = \frac{l}{2}$, ta có $$\frac{dy}{dx}=0\tag{10}$$ Chọn mốc thế năng tại $\text{C}$, áp dụng định luật bảo toàn cơ năng ở $\text{O}$ và $\text{C}$ ta có \begin{align} \frac{1}{2}mv^2=mgh\tag{11}\\ \Rightarrow\ v^2=2gh=\frac{2gl}{3}\tag{12} \end{align} Phương trình động lực học tại $\text{C}$: $$N-mg=\frac{mv^2}{r}\tag{13}$$ Trong đó $r$ là bán kính cong của quỹ đạo tại $\text{C}$, nó được tính bằng công thức $$r=\frac{\left[1+\left(\frac{dy}{dx}\right)^2\right]}{\frac{d^2y}{dx^2}}\tag{14}$$ Với $\frac{dy}{dx}=0$ và \begin{align} \frac{d^2y}{dx}&=-\frac{\pi^2h}{l^2}\sin{\left(\frac{\pi x}{l}\right)}\\ &=-\frac{\pi^2}{3l}\tag{15} \end{align} Dấu ‘-‘ chỉ có ý nghĩa rằng bề lõm của quỹ đạo tại $\text{C}$ quay lên trên, ta chỉ lấy độ lớn của bán kính cong $$r=\frac{3l}{\pi^2}\tag{16}$$ Khi đó áp lực lên máng \begin{align} N&=mg+\frac{mv^2}{r}\\ &=m\left(g+\frac{2gl}{3}.\frac{\pi^2}{3l}\right)\\ &=mg\left(1+\frac{2\pi^2}{9}\right)\tag{17} \end{align}Bài 2
Một lượng lớn thấu kính hội tụ mỏng có tiêu cự $f$ được đặt cách đều nhau khoảng $l$ sao cho trục chính của tất cả thấu kính trùng nhau. Khoảng $l$ nhỏ hơn rất nhiều so với $f$. Một chùm sáng chiếu vuông góc tới mặt phẳng thấu kính thứ nhất (hình vẽ dưới đây). Hãy vẽ tiếp tia sáng và xác định khoảng cách giữa các điểm tia sáng cắt trục chính của hệ lần thứ ba và lần thứ tư.

Giải
Các tia sáng hội tụ nên bẻ cong dần về phía trục chính. Sau khi cắt trục chính, chúng lại hội tụ theo hướng ngược lại,… cứ như vậy tia sáng có dạng tuần hoàn như hình vẽ.Ta chứng minh tia sáng có dạng hình sin.


Và do tại đó $y$ đang giảm nên $dy\lt0$, ta có \begin{align} \tan{\alpha}&=-\frac{dy}{dx}\\ &=-f^\prime\left(x\right)\tag{19} \end{align} Tương tự \begin{align} \tan{\beta}&=-f^\prime\left(x+l\right)\\ &=-f^\prime\left(x+dx\right)\tag{20} \end{align} Thay trở lại biểu thức mới tìm \begin{align} \tan{\alpha}-\tan{\beta}=-\frac{y}{f}\tag{21}\\ f^\prime\left(x+dx\right)-f^\prime\left(x\right)=-\frac{y}{f}\tag{22} \end{align} Chia cả hai vế cho $l$, nhưng ở vế trái ta xem $l = dx$ $$\frac{f^\prime\left(x+dx\right)-f^\prime\left(x\right)}{dx}=-\frac{y}{lf}\tag{23}$$ Vế trái chính là đạo hàm bậc hai của $y$ theo $x$ $$y^{\prime\prime}=-\frac{1}{lf}y\tag{24}$$ Phương trình vi phân quen thuộc này suy ra được \begin{align} y=y_0\cos{\left(\omega x\right)}\tag{25}\\ \omega=\sqrt{\frac{1}{lf}}\tag{26} \end{align} Tức là đường truyền các tia sáng có dạng hình sin, nhận $Ox$ làm trục đối xứng.

Bài 3
- Hãy xác định dạng quỹ đạo chuyển động cuả quả cầu (B).
- Tính áp lực của thanh lên quả cầu (A) và lực căng sợi dây khi quả cầu (B) ở vị trí thấp nhất.

Giải
1. Dạng quỹ đạo chuyển động của quả cầu (B)Chọn hệ trục tọa độ $xOy$ sao cho, $O$ ở trung điểm của thanh, $Ox$ trùng với thanh hướng sang phải, $Oy$ thẳng đứng hướng xuống. Áp dụng định luật bảo toàn động lượng cho hệ hai quả cầu theo phương ngang ta có \begin{align} mv_A+mv_{Bx}=0\tag{30}\\ \Rightarrow\ v_{xB}={-v}_A\tag{31} \end{align} tức là $x_A=-x_B$ ở mọi thời điểm, và ta có $$y^2+\left(2x\right)^2=L^2\tag{32}$$ Hay $$\frac{x^2}{\left(\frac{L}{2}\right)^2}+\frac{y^2}{L^2}=1\tag{33}$$ Đây là phương trình của một êlip.
2. Áp lực của thanh lên quả cầu (A) và lực căng sợi dây

Bài 4
Một vật khối lượng $2m$ được coi là chất điểm đặt ở đỉnh của một đường trượt (C) có dạng parabol với phương trình trong hệ toạ độ $oxy$ (trong mặt phẳng thẳng đứng như hình vẽ dưới đây): $y=Ax^2 \text{(m)}$; $A=20\ \left(m^{-1}\right)$, $x$ tính bằng m . Một viên đạn khối lượng $m$ bay theo phương ngang với vận tốc $v_0$ đến va chạm mềm với chất điểm nói trên. Tìm điều kiện $v_0$ để vật luôn trượt trên đường (C) nói trên . Bỏ qua ma sát.

Giải
Giả sử sau khi va chạm, vật trượt trên đường trượt, tại tọa độ $x, y$ bất kì ta có
Bài 5
Một vệ tinh nhân tạo khối lượng m chuyển động theo quỹ đạo êlíp quanh Trái Đất. Khoảng cách từ tâm Trái Đất đến vị trí gần nhất và xa nhất của vệ tinh là h và H. Biết khối lượng của Trái Đất là M. Xác định tốc độ dài của vệ tinh khi nó đi qua vị trí cách đều hai tiêu điểm của êlíp.
Giải
Chọn hệ trục tọa độ xOy như hình vẽ.
Khi đó ta có \begin{align} y=&\sqrt{A-Bx^2}\tag{60}\\ \frac{dy}{dx}&=-\frac{Bx}{\sqrt{A-Bx^2}}\tag{61}\\ \frac{d^2y}{dx^2}&=-\frac{B}{\sqrt{A-Bx^2}}-\frac{B^2x}{\sqrt{\left(A-Bx^2\right)^3}}\\ &=-\frac{B}{\sqrt{A-Bx^2}}\left(1+\frac{Bx}{A-Bx^2}\right)\tag{62} \end{align} Tại tọa độ $x = 0$ thì \begin{align} y^\prime\left(0\right)&=0\tag{63}\\ y^{\prime\prime}\left(0\right)&=-\frac{B}{\sqrt\ A}\\ &=-\frac{4\sqrt{Hh}}{\left(H+h\right)^2}\tag{64} \end{align} Độ cong của quỹ đạo tại đó là \begin{align} \frac{1}{r}&=\frac{y^{\prime\prime}\left(0\right)}{\left[1+\left(y^\prime\left(0\right)\right)^2\right]^\frac{3}{2}}\\ &=-\frac{4\sqrt{Hh}}{\left(H+h\right)^2}\tag{65} \end{align} Dấu "$-$" chỉ cho ta biết bề lõm quỹ đạo quay xuống, ta chỉ cần lấy độ lớn khi tính lực pháp tuyến.
Lực pháp tuyến tác dụng lên vệ tinh chính là một thành phần của lực hấp dẫn giữa vệ tinh và Trái Đất, ta có $$G\frac{mM}{R^2}.cos\alpha=\frac{mv^2}{r}\tag{66}$$ Trong đó \begin{align} R&=\frac{H+h}{2}\\ \mathrm{và}\\ \cos{α}&=\frac{b}{R}\\ &=\frac{2\sqrt{Hh}}{H+h}\tag{67} \end{align} Thay vào phương trình trên ta suy ra được $$v=\sqrt{\frac{2GM}{H+h}}\tag{68}$$
Bài tập tự giải
Bài 1
Một thanh kim loại AB cứng, mảnh, được uốn sao cho trùng với đồ thị hàm số $y = ax^2$, $0 ≤ x ≤ x_m$, với $x_m = 0\text{,}5\ \text{m}$ là tọa độ của đầu B của thanh, $a = 5\ \text{m}^{-1}$ (hình vẽ). Một hạt nhỏ khối lượng $m = 500\ \text{g}$ được lồng vào thanh, hạt có thể chuyển động tới mọi điểm trên thanh. Mặt phẳng $xOy$ thẳng đứng, $Oy$ thẳng đứng đi lên, thanh được giữ cố định. Thả nhẹ vật từ B để nó trượt không ma sát dọc theo thanh. Tính gia tốc của vật và áp lực của vật lên thanh tại tọa độ $x = 0\text{,}2\ \text{m}$. Lấy $g = 10\ \text{m/s}^2$ và bỏ qua ma sát.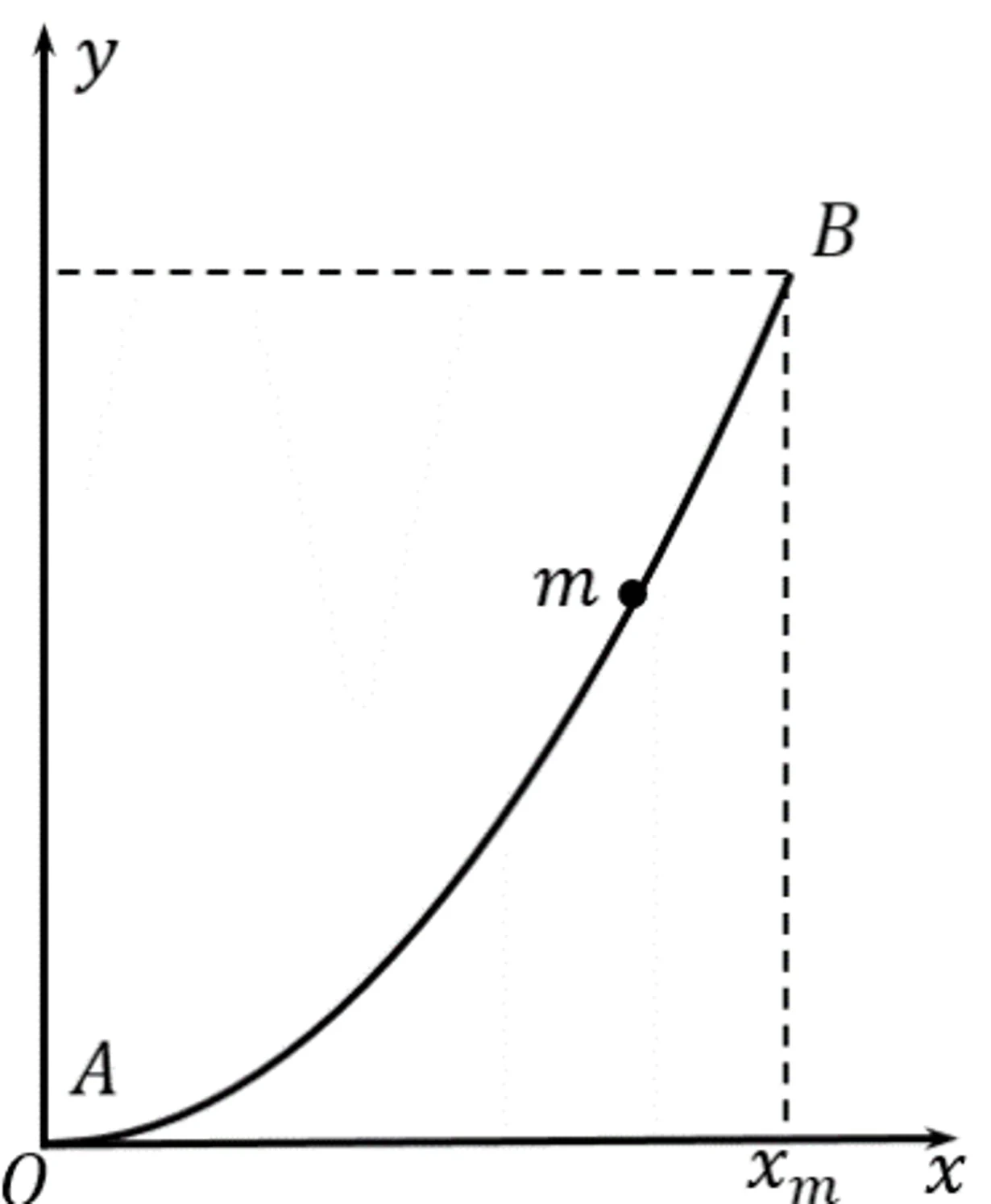
ĐS: 11,62 N
Bài 2
Người ta vẽ lại quỹ đạo của hòn đá được ném với vận tốc $20\ \text{m/s}$ và với một góc $45^0$ so với mặt đất lên một tờ giấy. Tỉ lệ vẽ là $1:10$ (giảm đi $10$ lần). Có một con bọ bò theo quĩ đạo được vẽ trên giấy này với vận tốc không đổi $0\text{,}02\ \text{m/s}$. Hãy tính gia tốc của con bọ tại điểm tương ứng với điểm cao nhất trên quĩ đạo của hòn đá.ĐS: $2\times10^{-4}\ \text{m/s}^2$
Bài 3
Một con tàu vũ trụ được phóng lên chuyển động quanh trái đất theo quỹ đạo êlíp có bán trục lớn $a$, bán trục nhỏ $b$. Biết trái đất có khối lượng $M$ và nằm một trong hai tiêu điểm êlíp. Hãy xác định vận tốc của tàu tại cận điểm $\text{A}$ và viễn điểm $\text{B}$.ĐS: $v_A = \frac{b}{a - \sqrt{a^2 - b^2}}\times\sqrt{\frac{GM}{a}}$; $v_B = \frac{b}{a + \sqrt{a^2 - b^2}}\times\sqrt{\frac{GM}{a}}$
Bài 4
Trên một mặt phẳng ngang có một chiếc nêm khối lượng $m$ mà mặt cắt của nó có dạng parabol với phương trình trong hệ toạ độ $oxy$ (trong mặt phẳng thẳng đứng như hình vẽ): $y = ax^2\ \text{(m)}$; $a = 5\ \text{m}$, $x$ tính bằng $\text{m}$. Một vật nhỏ khối lượng $m$ chuyển động trên mặt phẳng ngang rồi trượt lên nêm, vận tốc của vật lúc tiếp xúc với nêm là $v_0 = 4\ \text{m/s}$. Khi vật nhỏ có tọa độ $x = 0\text{,}5\ \text{m}$ thì nêm bắt đầu trượt trên mặt phẳng ngang. Lấy $g = 10\ \text{m/s}^2$ và bỏ qua ma sát giữa nêm với vật nhỏ. Tính hệ số ma sát trượt giữa nêm và mặt phẳng ngang.
ĐS: $\mu=0\text{,}12$


0 nhận xét:
Đăng nhận xét